Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
14th Edition
ISBN: 9780134677972
Author: Barnett
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 9.1, Problem 17E
In Problems 15-20, use the transition diagram
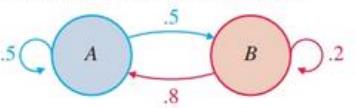
to find
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
15C. Use the transition diagram to express the stochastic matrix corresponding to
the states and transitions represented in this system.
O
1519
0.8
L
A
B
0.8 0.2
0.7 0.3
A B
0.3 0.2
0.7 0.8
A
www
AB
A B
0.7 0.8 А
0.3 0.2
The
A
B
B
0.8 0.3
A
0.2 0.7 B
AB
A
B
0.3 0.7
A
0.2 0.8 B
P
A
0.2
0.3
B
0.7
Consider a communication channel where each
substation transmits and receive data. The probability
between the substations is shown in figure 3.
0.4
0.5
0.3
0.2
2
2
0.3
Figure 3
i. Draw a transition diagram.
ii. Write down a transition matrix, P.
iii. Name the type of matrix in Q3(b)
P(X, =2 X, = 1|X, =3)
iv.
P(X, =2 X, = 3X, =2)
V.
en
Can someone please help me with these two questions. I am having so much trouble.
Chapter 9 Solutions
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Ch. 9.1 - (A) Refer to the transition diagram in Figure 1....Ch. 9.1 - Refer to Example 4. States D and G are referred to...Ch. 9.1 - An insurance company classifies drivers as...Ch. 9.1 - Find P4 and use it to find S4 for AAP=AA.8.2.3.7...Ch. 9.1 - Use P8 and a graphing calculator to find S8 for P...Ch. 9.1 - Refer to Example 4. At the end of each year the...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...
Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - Draw the transition diagram that corresponds to...Ch. 9.1 - Find the transition matrix that corresponds to the...Ch. 9.1 - Draw the transition matrix that corresponds to the...Ch. 9.1 - Find the transition diagram that corresponds to...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - Prob. 42ECh. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 51-56, are there unique values of a,b,...Ch. 9.1 - In Problems 51-56, are there unique values of a,b,...Ch. 9.1 - In Problems 51-56, are there unique values of a,b,...Ch. 9.1 - Prob. 54ECh. 9.1 - In Problems 51-56, are there unique values of a,b,...Ch. 9.1 - Prob. 56ECh. 9.1 - In Problems 57-60, use the given information to...Ch. 9.1 - A Markov chain has two states, A and B. The...Ch. 9.1 - Prob. 59ECh. 9.1 - Prob. 60ECh. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Prob. 65ECh. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Prob. 67ECh. 9.1 - Prob. 68ECh. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - In Problems 71-74, given the transition matrix P...Ch. 9.1 - In Problems 71-74, given the transition matrix P...Ch. 9.1 - In Problems 71-74, given the transition matrix P...Ch. 9.1 - In Problems 71-74, given the transition matrix P...Ch. 9.1 - A Markov chain with two states has transition...Ch. 9.1 - Repeat Problem 75 if the initial-state matrix is...Ch. 9.1 - Given the transition matrix...Ch. 9.1 - Prob. 78ECh. 9.1 - Show that if P=a1a1bb is probability matrix, then...Ch. 9.1 - Show that if P=a1a1bbandS=c1c are probability...Ch. 9.1 - Use a graphing calculator and the formula Sk =...Ch. 9.1 - Use a graphing calculator and the formula Sk=S0Pk...Ch. 9.1 - Use a graphing calculator and the formula Sk=S0Pk...Ch. 9.1 - Use a graphing calculator and the formula Sk=S0Pk...Ch. 9.1 - Scheduling. An outdoor restaurant in a summer...Ch. 9.1 - Scheduling. Repeat Problem 85 if the probability...Ch. 9.1 - Advertising. A television advertising campaign is...Ch. 9.1 - Car rental. A car rental agency has facilities at...Ch. 9.1 - Homeowner's insurance. In a given city, the market...Ch. 9.1 - Service contracts. A small community has two...Ch. 9.1 - Travel agent training. A chain of travel agencies...Ch. 9.1 - Welder training. All welders in a factory begin as...Ch. 9.1 - Health plans. A midwestern university offers its...Ch. 9.1 - Dental insurance. Refer to Problem 93. During the...Ch. 9.1 - Housing trends. The 2000 census reported that 41.9...Ch. 9.1 - Housing trends. The 2000 census reported that 66.4...Ch. 9.2 - (A) Suppose that the toothpaste company started...Ch. 9.2 - Which of the following matrices are regular? (A)...Ch. 9.2 - The transition matrix for a Markov chain is...Ch. 9.2 - Refer to Matched Problem 1 in Section 9.1, where...Ch. 9.2 - A mail-order company classifies its customers as...Ch. 9.2 - Repeat Example 5 for P=.3.6.1.2.3.5.1.2.7Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - Prob. 13ECh. 9.2 - Prob. 14ECh. 9.2 - Prob. 15ECh. 9.2 - Prob. 16ECh. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - Problems 31-34 refer to the regular Markov chain...Ch. 9.2 - Problems 31-34 refer to the regular Markov chain...Ch. 9.2 - Problems 31-34 refer to the regular Markov chain...Ch. 9.2 - Problems 31-34 refer to the regular Markov chain...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 41-44, approximate the stationary...Ch. 9.2 - In Problems 41-44, approximate the stationary...Ch. 9.2 - In Problems 41-44, approximate the stationary...Ch. 9.2 - In Problems 41-44, approximate the stationary'...Ch. 9.2 - A red urn contains 2 red marbles and 3 blue...Ch. 9.2 - Repeat Problem 45 if the red urn contains 5 red...Ch. 9.2 - Given the transition matrix P=0110 A) Discuss the...Ch. 9.2 - Given the transition matrix P=001100010 (A)...Ch. 9.2 - The transition matrix for a Markov chain is...Ch. 9.2 - The transition matrix for a Markov chain is...Ch. 9.2 - Problems 51 and 52 require the use of a graphing...Ch. 9.2 - Problems 51 and 52 require the use of a graphing...Ch. 9.2 - The transition matric for a Markov chain is...Ch. 9.2 - The transition matric for a Markov chain is...Ch. 9.2 - Transportation. Most railroad cars are owned by...Ch. 9.2 - Transportation. The railroad in Problem 55 also...Ch. 9.2 - Labor force. Table 1 gives the percentage of the...Ch. 9.2 - Home ownership. The U.S. Census Bureau published...Ch. 9.2 - Market share. Consumers can choose between three...Ch. 9.2 - Market share. Consumers in a certain area can...Ch. 9.2 - Insurance. An auto insurance company classifies...Ch. 9.2 - Insurance. Repeat Problems 61 if 40 of preferred...Ch. 9.2 - Problems 63 and 64 require the use of a graphing...Ch. 9.2 - Problems 63 and 64 require the use of a graphing...Ch. 9.2 - Genetics. A given plant species has red, pink, or...Ch. 9.2 - Gene mutation. Suppose that a gene in a chromosome...Ch. 9.2 - Rapid transit. A new rapid transit system has just...Ch. 9.2 - Politics: filibuster. The Senate is in the middle...Ch. 9.2 - The population center of the 48 contiguous states...Ch. 9.2 - The population center of the 48 contiguous states...Ch. 9.3 - (A) For the initial-state matrix S0=abc, find the...Ch. 9.3 - Determine whether each statement is true or false....Ch. 9.3 - Identify any absorbing states for the following...Ch. 9.3 - Use a transition diagram to determine whether P is...Ch. 9.3 - Repeat Example 3 if 10 of farmers sell to company...Ch. 9.3 - Repeat Example 4 for the standard form P found in...Ch. 9.3 - Repeat Example 5 for the following transition...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 7-10, identify the absorbing states...Ch. 9.3 - In Problems 7-10, identify the absorbing states...Ch. 9.3 - In Problems 7-10, identify the absorbing states...Ch. 9.3 - In Problems 7-10, identify the absorbing states...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 21-24.find a standard form for the...Ch. 9.3 - In Problems 21-24.find a standard form for the...Ch. 9.3 - In Problems 21-24.find a standard form for the...Ch. 9.3 - In Problems 21-24.find a standard form for the...Ch. 9.3 - In Problems 25-28, find a standard form for the...Ch. 9.3 - In Problems 25-28, find a standard form for the...Ch. 9.3 - In Problems 25-28, find a standard form for the...Ch. 9.3 - In Problems 25-28, find a standard form for the...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 49-52, use a graphing calculator to...Ch. 9.3 - In Problems 49-52, use a graphing calculator to...Ch. 9.3 - In Problems 49-52, use a graphing calculator to...Ch. 9.3 - In Problems 49-52, use a graphing calculator to...Ch. 9.3 - The following matrix P is a nonstandard transition...Ch. 9.3 - Repeat Problem 53 for...Ch. 9.3 - Verify the results in Problem 53 by computing Pk...Ch. 9.3 - Verify the results in Problem 54 by computing Pk...Ch. 9.3 - Show that S=x1x0,0x1, is a stationary matrix for...Ch. 9.3 - Show that S=x1x00,0x1, is a stationary matrix for...Ch. 9.3 - An absorbing Markov chain has the following matrix...Ch. 9.3 - Refer to the matrices P and Q of Problem 59. For k...Ch. 9.3 - Loans. A credit union classifies car loans into...Ch. 9.3 - Employee training. A chain of car muffler and...Ch. 9.3 - Marketing. Three electronics firms are...Ch. 9.3 - Pensions. Once a year company employees are given...Ch. 9.3 - Medicine. After bypass surgery, patients are...Ch. 9.3 - Medicine. The study discussed in Problem 65 also...Ch. 9.3 - Psychology. A rat is placed in room F or room B of...Ch. 9.3 - Psychology. Repeat Problem 67 if the exit from...Ch. 9 - Given the transition matrix P and initial-state...Ch. 9 - In Problems 2-6, P is a transition matrix for a...Ch. 9 - In Problems 2-6, P is a transition matrix for a...Ch. 9 - In Problems 2-6, P is a transition matrix for a...Ch. 9 - In Problems 2-6, P is a transition matrix for a...Ch. 9 - Prob. 6RECh. 9 - In Problems 7-10, write a transition matrix for...Ch. 9 - In Problems 7-10, write a transition matrix for...Ch. 9 - In Problems 7-10, write a transition matrix for...Ch. 9 - In Problems 7-10, write a transition matrix for...Ch. 9 - A Markov chain has three states, A,B, and C. The...Ch. 9 - Given the transition matrix ABP=AB.4.6.9.1 find...Ch. 9 - In Problems 13 and 14. solve the equation SP=S to...Ch. 9 - In Problems 13 and 14. solve the equation SP=S to...Ch. 9 - In Problems 15 and 16, find the limiting matrix...Ch. 9 - In Problems 15 and 16, find the limiting matrix...Ch. 9 - In Problems 17-20, use a graphing calculator to...Ch. 9 - In Problems 17-20, use a graphing calculator to...Ch. 9 - In Problems 17-20, use a graphing calculator to...Ch. 9 - In Problems 17-20, use a graphing calculator to...Ch. 9 - Find a standard form for the absorbing Markov...Ch. 9 - In Problems 22 and 23, determine the long-run...Ch. 9 - In Problems 22 and 23, determine the long-run...Ch. 9 - Let P be a 22 transition matrix for a Markov...Ch. 9 - Let P be a 33 transition matrix for a Markov...Ch. 9 - A red urn contains 2 red marbles, 1 blue marble,...Ch. 9 - Repeat Problem 26 if the blue and green marbles...Ch. 9 - Show that S=xyz0, where 0x1, 0y1, 0z1, and...Ch. 9 - Give an example of a transition matrix for a...Ch. 9 - Give an example of a transition matrix for an...Ch. 9 - Give an example of a transition matrix for a...Ch. 9 - Give an example of a transition matrix for an...Ch. 9 - Explain why an absorbing Markov chain that has...Ch. 9 - Explain why a regular Markov chain that has more...Ch. 9 - A Markov chain has transition matrix P=.4.6.2.8...Ch. 9 - In Problems 36 and 37, use a graphing calculator...Ch. 9 - In Problems 36 and 37, use a graphing calculator...Ch. 9 - Product switching. A company's brand X has 20 of...Ch. 9 - Marketing. Recent technological advances have led...Ch. 9 - Prob. 40RECh. 9 - Employee training. In order to become a fellow of...Ch. 9 - Genetics. A given plant species has red, pink, or...Ch. 9 - Smoking. Table 2 gives the percentage of U.S....
Additional Math Textbook Solutions
Find more solutions based on key concepts
69. Get Started Early! Mitch and Bill are both age 75. When Mitch was 25 years old, he began depositing $1000 p...
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Checkpoint1
Use the substitution method to solve this system:
Answers to Checkpoint exercises are found at the...
Mathematics with Applications In the Management, Natural, and Social Sciences (12th Edition)
Family Library The Venn diagram in Fig. 10 classifies the 100 books in a familys library as hardback (H), ficti...
Finite Mathematics & Its Applications (12th Edition)
In Exercises 1-12, use set notation to list all the elements of each set. The natural numbers from 10 to 15 inc...
Mathematics All Around (6th Edition)
The equivalent expression of x(y+z) by using the commutative property.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Explain why commands and questions are not statements.
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Consider a communication channel where each substation transmits and receive data. The probability between the substations is shown in figure 3. 0.4 0.5 0.3 0.2 2 2 3 0.3 Figure 3 i. Draw a transition diagram. ii. Write down a transition matrix, P. iii. Name the type of matrix in Q3(b) P(X; =2 X,=1\X, =3) iv. P(X; =2 _X,=3{X, =2) V.arrow_forward5. consider the example below, where the states are Condition State and the transition matrix is 0 1 23 2 Πο Good as new Operable-minimum deterioration Operable-major deterioration Inoperable and replaced by a good-as-new machine we found that the steady-state probabilities are 2 13' T1= = P = 78314 00 1 0 7 13' HARTNO LELBLINO 1 16 1 1 1 1 16 8 8 0 2 2 = π2 2 13' I3 = 2 13 (a) Find the expected recurrence time for state 0 (i.e., the expected length of time a machine can be used before it must be replaced) by solving a linear system for Moo, M10, 20, and μ30. (b) Find the expected recurrence time for state O directly by the formula Moo 1 πο =arrow_forward64. Employee training. All welders in a factory begin as apprentices. Every year the performance of each appren- tice is reviewed. Past records indicate that after each review, 10% of the apprentices are promoted to profes- sional welder, 20% are terminated for unsatisfactory per- formance, and the remainder continue as apprentices. (A) Draw a transition diagram. (B) Write the transition matrix. (C) What is the probability that an apprentice is promoted to professional welder within 2 years? Within 4 years?arrow_forward
- c. The market share of two companies A and B is 30% and 70% in the current time period. The information obtained in terms of the customer loss and retention is given by the matrix P. [0.3 0.2] P = Lo.7 0.8] i.Determine the transition probability matrix in the 1st and 2nd month. ii.What is the steady state of the two companies?arrow_forwardlay. 1.8. Consider the following transition matrices. Identify the transient and recurrent states, and the irreducible closed sets in the Markov chains. Give reasons for your answers. (a) 1 2 3 4 5 12345 .4 .3 .3 00 0.5 0 .5 O 0 3 .5 0.5 0 4 0.5 0.5 0 5 0.3 0 .3 .4 1 2 3 (c) 1 2 3 4 5 00001 0.2 0.8 0 .1 .2 .4 .3 0 4 0.4 0.6 0 5.2 0 0 0.8 1 6 0.3 0.3 0.4 3 4 5 1 0 0 0 0 2/3 0 1/3 0 1/8 1/4 5/8 0 0 0 1/6 O 5/6 0 5 1/3 0 1/3 0 1/3 (e) 1 2 3 4 (b) 1 2 3 456 1 .1 0 0 .4 .5 O 2 .1 .2.2 0.5 0 3 0.1.3 0 0.6 4.10 0.90 0 5 0 0 TO 4 0 6 6 000 0.5.5 (d) 1 2 3 4 5 6 1.8 0 0.20 0 20.50 0.5 0 3 0 0 .3 .4 .1 .2 4.10 0.90 0 50.200.80 2 0arrow_forwardWhat is the solution to these two problems?arrow_forward
- 4. Suppose that the following data were obtained from the records of a certain two year college: Of those who were freshman (F) during a particular year, 80% become sopho- mores (S) during the next year and 20% dropped out. Of those who were sophomores during a particular year 90% graduated (G) by the next year and 10% dropped out. (a) Create a transition diagram that describes this scenario. (b) Create a transition matrix that describes this scenario. Is this scenario ergodic or absorbing? Explain. (c) Suppose that this year, there are an equal percentage of freshmen and sophomores. Use matrix multiplication to determine what percentage will have graduated in 5 years? What percentage will have dropped out? (d) Rewrite the matrix in standard form. (e) Find N, R and B. (f) Determine the probability that a student who begins as a freshman will drop out. (g) Determine the probability that a student who has made it to sophomore year will drop out. (h) Determine the probability that a…arrow_forward. Suppose that a Markov chain with 3 states and with transition matrix P is in state 2 onthe second observation. Which of the following expressions represents the probabilitythat it will be in state 3 on the third observation? (A) the (2, 3) entry of P 3 (B) the (2, 3) entry of P 2(C) the (3, 3) entry of P 2 (D) the (2, 2) entry of P 3(E) the (2, 3) entry of P (F) the (3, 2) entry of P(G) the (3, 2) entry of P 3 (H) the (3, 2) entry of P 2arrow_forwardQ2. Consider a company that is going to build a new manufacturing system and would like to determine the long-run (steady-state) mean hourly throughput of their system after it has been running long enough for workers to know their jobs and for mechanical difficulties to have been worked out. The system will operate continuously 24 hours a day for 7 days a week. Let N; be the number of parts manufactured in the ih hour. If the stochastic process N1, N2, .. has a steady-state distribution with corresponding random variable N, then we are interested in estimating the steady-state mean v = E(N).arrow_forward
- 3. Construct a model of population flows between cities, suburbs, and nonmetropolitan areas of the United States. Their respective populations in 2022 were 80 million, 175 million, and 52 million. The stochastic matrix giving the probabilities of the moves is (from) (to) city suburb nonmetro 0.96 0.01 0.015 city 0.03 0.98 0.005 suburb 0.01 0.01 0.98 nonmetro Predict the populations of city, suburban, and nonmetropolitan areas for 2023, 2024, and 2025. If a person was living in the city in 2022, what is the probability the person will be living in a nonmetropolian area in 2024?arrow_forwardExample 4: The number of defects on 20 items are given below Item No. 1 2 3 4 5 6 78 9 10 11 12 13 14 15 16 17 18 19 20 No. of defects 2 0 4 1 0 8 0 1 2 0 6 0 2 1 0 3 2 1 0 2 Devise a suitable control scheme for the future.arrow_forwardIn an office complex of 1100 employees, on any given day some are at work and the rest are absent. It is known that if an employee is at work today, there is an 80% chance that she will be at work tomorrow, and if the employee is absent today, there is a 51% chance that she will be absent tomorrow. Suppose that today there are 913 employees at work. .80 .49 ( a) Find the transition matrix for this scenario. .2 .51 (b) Predict the number that will be at work five days from now. 781.5 2.45 (c) Find the steady-state vector. .29arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Finite Math: Markov Chain Example - The Gambler's Ruin; Author: Brandon Foltz;https://www.youtube.com/watch?v=afIhgiHVnj0;License: Standard YouTube License, CC-BY
Introduction: MARKOV PROCESS And MARKOV CHAINS // Short Lecture // Linear Algebra; Author: AfterMath;https://www.youtube.com/watch?v=qK-PUTuUSpw;License: Standard Youtube License
Stochastic process and Markov Chain Model | Transition Probability Matrix (TPM); Author: Dr. Harish Garg;https://www.youtube.com/watch?v=sb4jo4P4ZLI;License: Standard YouTube License, CC-BY