
(a)
Interpretation:
The pouring temperature in the cooling curve needs to be determined.
Concept Introduction:
The cooling curve represents a change in temperature as a function of time. Cooling curve is of two types: Curve for metals having no inoculation and curve for metals with inoculation.
Answer to Problem 9.61P
Pouring temperature is
Explanation of Solution
The figure shows the cooling curve for casting.
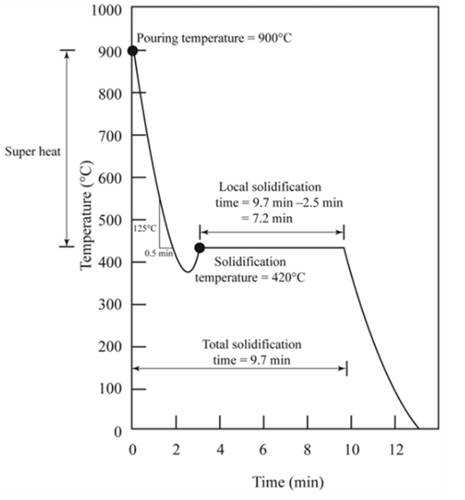
Pouring temperature is the temperature of the liquid at which liquid is added in the mold.Hence from the graph shown, temperature
(b)
Interpretation:
Solidification temperature of the metal in cooling curves needs to be determined.
Concept Introduction:
Solidification is a process of forming crystal structure from molten metal during cooling.The temperature at which molten metal starts forming crystal is solidification temperature.
Answer to Problem 9.61P
Solidification temperature of metal is
Explanation of Solution
Solidification temperature at which solidification starts.Hence from the graph, solidification temperature is
Or,
(c)
Interpretation:
The superheat temperature of the metal needs to be determined.
Concept Introduction:
Difference between pouring temperature and freezing temperature is known as superheating.
Pouring temperature is the temperature at which metal is introduced in a casting.
Freezing temperature is the temperature at which metal solidifies.
Answer to Problem 9.61P
Superheat temperature is
Explanation of Solution
Superheat is a temperature between pouring temperature and freezing temperature.
Pouring temperature,
Freezing temperature,
Thus,
(d)
Interpretation:
At the starting of the solidification, thecooling rate needs to be determined.
Concept Introduction:
Cooling curves are of two types of metal- for metal with no inoculation and for metal with inoculation.
Cooling curve represents different temperatures.
The cooling curve shows different regions according to change in temperature at a specific time.
Answer to Problem 9.61P
Cooling rate of metal is
Explanation of Solution
The cooling rate is the rate of change in temperature with respect to time.
According to the graph,the slope of the curve from pouring temperature to freezing temperature shows the rate of cooling.
It is denoted by
Thus,
Cooling rate
(e)
Interpretation:
The total solidification time needs to be determined.
Concept Introduction:
Solidification is a process of forming crystal structure from molten metal during cooling. The time required to form crystal structure from molten metal is solidification time.
Answer to Problem 9.61P
Total solidification time of metal is
Explanation of Solution
The time required to remove specific heat and latent heat of fusion during cooling of metal is total solidification time.It is the time between the pouring of metal to the completion of solidification.
From the graph,
(f)
Interpretation:
The local solidification time of metal needs to be determined.
Concept Introduction:
Solidification is a process of forming crystal structure from molten metal during cooling. The time required to form crystal structure from molten metal is solidification time.
Answer to Problem 9.61P
Local solidification time of metal is 7.2 min.
Explanation of Solution
The time required to remove latent heat of fusion is at specific casting location is local solidification time.
It is the time between the start of solidification and the end of solidification.
Hence from the graph,
(g)
Interpretation:
The identity of metal needs to be determined.
Concept Introduction:
Cooling curves are of two types of metal- for metal with no inoculation and for metal with inoculation.
Cooling curve represents different temperatures.The cooling curve represents charge in temperature as a function of time.
Answer to Problem 9.61P
Probable metal should be Zinc.
Explanation of Solution
Given the cooling curve is for metal having well inoculation.For this metal, solidification starts at melting temperature.Solidification of the temperature of this metal is
Hence, the probable metal should be zinc.
(h)
Interpretation:
The mold constant of metal needs to be determined.
Concept Introduction:
As per Chvorinov's rule, solidification time is directly proportional to the square of volume- area ratio of cast metal.
Here,
Answer to Problem 9.61P
Mold constant is
Explanation of Solution
As per Chvorinov's rule,
Volume of casting can be calculated as follow:
Area of castingcan be calculated as follow:
Putting the value.
Want to see more full solutions like this?
Chapter 9 Solutions
Essentials of Materials Science and Engineering, SI Edition
- please solve this problem for me the best way that you can explained to solve please show me the step how to solvearrow_forwardplese solbe this problem and give the correct answer solve step by step find the forces and line actionarrow_forwardplease help me to solve this problems first write the line of action and them find the forces {fx=0: fy=0: mz=0: and them draw the shear and bending moment diagram. please explain step by steparrow_forward
- please solve this problem step by step like human and give correct answer step by steparrow_forwarda) A 14-ft. tall and12-ft.-8-in. long fully grouted reinforced masonry wall is constructed of 8-in.CMU. It is to be analyzed for out-of-plane loading. Construct thenP -nM curves for the wallwith the following three vertical reinforcement scenarios: (1) 10 No. 6 bars at 16 in. spacing,(2) 10 No. 5 bars at 16 in. spacing, and (3) 7 No. 4 bars at 24 in. spacing. The steel is Grade60 with a modulus of elasticity of 29,000 ksi, and the masonry has a compressive strength of2,000 psi. You may use Excel or Matlab to construct the curves. Also, show the maximumnPallowed by the code for each case.(b) For each of the above reinforcement scenarios, determine the maximum axial loads that arepermitted for the tension-controlled condition and transition condition.(c) Discuss how the amount of vertical reinforcement affects thenPn - Mn curve.arrow_forwardPROBLEM 11: Determine the force, P, that must be exerted on the handles of the bolt cutter. (A) 7.5 N (B) 30.0 N (C) 52.5 N (D) 300 N (E) 325 N .B X 3 cm E 40 cm cm F = 1000 N 10 cm 3 cm boltarrow_forward
- Using the moment-area theorems, determine a) the rotation at A, b) the deflection at L/2, c) the deflection at L/4. (Hint: Use symmetry for Part a (θA= - θB, or θC=0), Use the rotation at A for Parts b and c. Note that all deformations in the scope of our topics are small deformation and for small θ, sinθ=θ).arrow_forwardDistilled water is being cooled by a 20% propylene glycol solution in a 1-1/U counter flow plate and frame heat exchanger. The water enters the heat exchanger at 50°F at a flow rate of 86,000 lbm/h. For safety reasons, the water outlet temperature should never be colder than 35°F. The propylene glycol solution enters the heat exchanger at 28°F with a flow rate of 73,000 lbm/h. The port distances on the heat exchanger are Lv = 35 in and Lh = 18 in. The plate width is Lw = 21.5 2 in. The plate thickness is 0.04 in with a plate pitch of 0.12 in. The chevron angle is 30° and the plate enlargement factor is 1.17. All ports have a 2 in diameter. The fouling factor of the propylene glycol solution can be estimated as 2 ×10−5 h-ft2-°F/Btu. a. Determine the maximum number of plates the heat exchanger can have while ensuring that the water outlet temperature never drops below 35°F. b. Determine the thermal and hydraulic performance of the heat exchanger with the specified number of plates.…arrow_forwardLiquid pentane is flowing in the shell of a shell and tube heat exchanger at a rate of 350,000lbm/hr and an average temperature of 20°F. The shell has a diameter of 27 in and a length of 16ft. The tubes in the heat exchanger are ¾-in 15 BWG tubes on a 1-in triangular pitch. The purposeof this problem is to investigate how the number of baffles impacts the heat transfer and thepressure drop on the shell side of the heat exchanger. Calculate the shell-side convective heattransfer coefficient and pressure drop for the case where the heat exchanger has 10 baffles. Repeatthe calculation for 20 baffles. Then determine thea. Ratio of the shell-side convective heat transfer coefficient for the 20-baffle heat exchangerto the 10-baffle heat exchangerb. Ratio of the shell-side pressure drop for the 20-baffle heat exchanger to the 10-baffle heatexchangerc. If the optimum baffle spacing is somewhere between 0.4Ds and 0.6Ds, how many baffleswould you recommend for this heat exchanger? What are the…arrow_forward
- Can you show why the answer is that for this question using second order differential equations, instead of laplace transformsarrow_forwardI need help to solve the following case, thank youarrow_forwardIf you could help me answer these questions in matlab that would be great, I provided an additional picture detailing what the outcome should look like.arrow_forward
 MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage,
Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage, Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning
Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION
Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON
Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY
Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY





