
Concept explainers
(a)
The point moves a greater distance in a given time, if the disk rotates with increasing
(a)
Answer to Problem 1P
The particle on the rim covers a greater linear distance as compared to the particle situated half way between the rim and the axis of rotation.
Explanation of Solution
Given:
A disk rotating with increasing angular velocity about an axis passing through its center and perpendicular to its plane.
Distance of the particle 1 (on the rim) from the axis of rotation
Distance of particle 2 (half way between the axis of rotation and the rim) from the axis of rotation
Here, the radius of the disk is
Formula used:
The
Here,
The angular acceleration of a point on the rotating disk is related to the linear acceleration
Here,
The linear distance
Calculations:
The disk of radius
from the axis of rotation. This is shown in the figure 1 below:
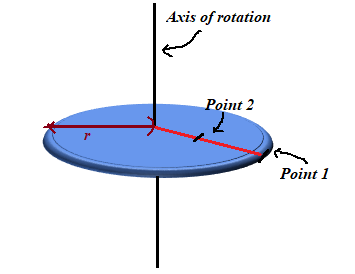
Figure 1
If the disk rotates with an angular acceleration
Calculate the linear accelerations of the particles located at point 1 and 2 using the equation (2).
Substitute
Therefore, from the above equations,
If the disk is assumed to start from rest, both particles would start with their initial velocities
Use equation (3) to calculate the distance travelled by the two points.
From equation (5),
Conclusion:
Therefore, the point on the rim travels a greater distance when compared to the point located halfway between the rim and the axis of rotation.
(b)
The point that turns through a greater angle.
(b)
Answer to Problem 1P
Both the points turn through the same angle.
Explanation of Solution
Formula used:
The
Here
Calculation:
The points 1 and 2 located at points A and B on the disc rotating with an angular acceleration
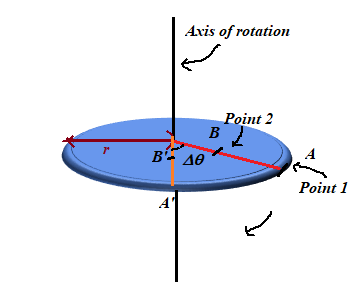
Figure 2
At any instant of time, both particles have the same instantaneous angular velocity and angular acceleration. As it can be seen from Figure 2, both particles describe the same angle at an instant of time.
Conclusion:
Thus, the particle located at the rim and the particle located half way between the rim and the axis of rotation turn through the same angle.
(c)
The point which travels with greater speed.
(c)
Answer to Problem 1P
The point on the rim travels with greater speed.
Explanation of Solution
Formula used:
The instantaneous speed
Here,
Calculation:
The disk moves with increasing angular velocity. But, both points at any instant would have the same instantaneous angular velocity, since they turn through the same angle in a given interval of time.
Hence, it can be inferred from equation (7):
Since the point on the rim has the greater value of
Conclusion:
Thus, the point on the rim would have a greater speed when compared to the point located half way between the rim and the axis of rotation.
(d)
The point which has the greater angular speed.
(d)
Answer to Problem 1P
Both the particles have the same angular speed.
Explanation of Solution
Formula used:
The angular velocity of a particle is given by
Calculation:
From Figure 2, it is seen that at any instant of time, both particles 1 and 2 cover the same angles. Hence, the rate of change of their angular displacement
Conclusion:
Thus, the particle on the rim and the particle located halfway between the rim and the axis of rotation have the same angular velocity.
(e)
The point which has the greater tangential acceleration.
(e)
Answer to Problem 1P
The point on the rim has a greater tangential acceleration when compared to the point located midway between the rim and the axis of rotation:
Explanation of Solution
Formula used:
The tangential acceleration
Calculation:
If the disk rotates with a varying angular velocity, it has angular acceleration. Assuming that the angular acceleration of the disk remains constant, from equation (9) it can be inferred that
The point on the rim has the greater value of
Therefore, the point on the rim has a greater tangential acceleration when compared to any point located inside the rim. This is also proved by the fact that the point on the rim gains a larger tangential velocity when compared to any inner point.
Conclusion:
Thus, the point on the rim has a greater tangential acceleration when compared to the point located midway between the rim and the axis of rotation.
(f)
The point which has a greater angular acceleration.
(f)
Answer to Problem 1P
Both particles have the same angular acceleration.
Explanation of Solution
Formula used:
The angular acceleration
Calculation:
It has been proved in (d) that at any instant of time, both the particles have the same angular velocity. Therefore, in an interval of time
Hence, from equation (1), it can be proved that at a given instant of time, both the points will have the same angular accelerations.
Conclusion:
Thus, both particles are found to have the same angular acceleration.
(g)
The point which has the greater centripetal acceleration.
(g)
Answer to Problem 1P
The point on the rim has a greater centripetal acceleration.
Explanation of Solution
Formula used:
The centripetal acceleration of a point located at a distance
Calculation:
It has been established in part (d) that at any instant of time, the point on the rim and the point located halfway between the rim and the axis of rotation have the same angular velocity.
Therefore, from equation (10), it can be inferred that
The point on the rim has the greater value of
Conclusion:
Thus, the point on the rim has a greater centripetal acceleration.
Want to see more full solutions like this?
Chapter 9 Solutions
PHYSICS F/SCI.+ENGRS.,STAND.-W/ACCESS
- d. when the index of refraction of medium A is equal to the index of refraction of medium B 7. What is the term for the bending of a wave front as it passes an obstacle? a. interference b. reflection C. d. diffraction refraction 8. A ray of light travels from air into a soap film on a layer of glass, as shown right. Which statement about ray 1 is true? a. There is no inversion at either surface. b. There is an inversion the surface between air and soap, but not soap and glass. C. There is no inversion at the surface between air and soap, incident light ray 1 ray 2 ray 3 but there is one at the surface between soap and glass. d. There is an inversion at both surfaces. air = nair 1.00 soap film nfilm = 1.35 glass = nglass 1.50arrow_forwardA circular wire with radius 0.4 meters in on x-y plane. There is a constant Magnetic field with 14T strengthtowards z-axis. Find the magnitude of the electromotive force and the direction of the current for a) B decreasesto 10T in 5 seconds. B) B is rotated by 45 degrees and the area doubles in 4 seconds.arrow_forwardWrite the expression for the magnetic flux inside a region om x-z plane at y=0 bounded by z=3x z=0 x=5 x=7due to a magnetic field B = f(x,y,z) i +g(x,y,z) j + h(x,y,z) karrow_forward
- Explain mutual inductance of two loops facing one another and compare with one loop inside the other.arrow_forwardTwo very long wires carry each 3 amps current in the same direction along the z-axis (outward). First is at x=0y=0 current is upward. Second at x=0 y=3 current is also upward. Find the net magnetic field at x=4 y=3.arrow_forwardFind the integral expression for the magnetic field at x=5 y=6 due to a wire on the x axis with length 5 meters onend at x=0 and the other at x=5. Don’t take the integralarrow_forward
- Two very long wires carry current along y-axis. First is at x=0 0.45 amps current is upward. Second at x=5 currentwith 0.65 amps current downward. Find the net magnetic a) Two meters to the left of the first wire. b) Twometers to the right of the first wire. a) Two meters to the right of the second wire. b) Two meters to the right ofthe second wire.arrow_forward! Required information The PV diagram shown is for a heat engine that uses 1.030 mol of a diatomic ideal gas as its working substance. In the constant-temperature processes A and C, the gas is in contact with reservoirs at temperatures 373 K and 273 K, respectively. In constant-volume process B, the gas temperature decreases as heat flows into the cold reservoir. In constant- volume process D, the gas temperature increases as heat flows from the hot reservoir. Pressure (kPa) 160 150 A 140 D 373 K 130 120 110 100 273 K C 90 80 B 0.019 0.02 0.021 0.022 0.023 0.024 0.025 0.026 Volume (m³) To compare the efficiency of the heat engine to that of an ideal engine, what is the ratio of the efficiency of an ideal engine using the same reservoirs to that of the heat engine, if the heat input per cycle is 2854 J?arrow_forward4 1.00 mol of oxygen gas (O2) is heated at a constant pressure of 1.00 atm from 10.0°C to 25.0°C. How much heat is absorbed by the gas? Multiple Choice О 389 J о 544 J О 436 J О 288 Jarrow_forward
- IL 6. For the sentence, why are the red lines representing the formants and the blue line representing the fundamental frequency always angled instead of horizontal?arrow_forwardCH 57. A 190-g block is launched by compressing a spring of constant k = = 200 N/m by 15 cm. The spring is mounted horizontally, and the surface directly under it is frictionless. But beyond the equilibrium position of the spring end, the surface has frictional coefficient μ = 0.27. This frictional surface extends 85 cm, fol- lowed by a frictionless curved rise, as shown in Fig. 7.21. After it's launched, where does the block finally come to rest? Measure from the left end of the frictional zone. Frictionless μ = 0.27 Frictionless FIGURE 7.21 Problem 57arrow_forward3. (a) Show that the CM of a uniform thin rod of length L and mass M is at its center (b) Determine the CM of the rod assuming its linear mass density 1 (its mass per unit length) varies linearly from λ = λ at the left end to double that 0 value, λ = 2λ, at the right end. y 0 ·x- dx dm=λdx x +arrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





