
Concept explainers
(a)
The angular speed of the ball just after the blow.
(a)
Answer to Problem 106P
Explanation of Solution
Given: The horizontal force applied on a billiard ball at a distance
Speed of the ball just after the blow is
The coefficient of kinetic friction between the ball and billiard table is
Formula Used:
Newton’s second law of motion in rotational form
Calculation:
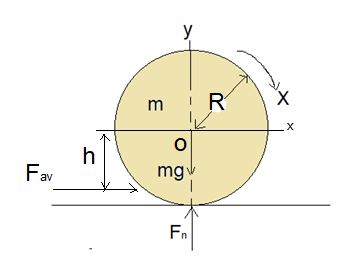
FIGURE: 1
Applying Newton’s second law in rotational form to ball,
Where,
Moment of inertia with respect to an axis through the center of mass of the ball is
Substituting this in equation
Applying impulse-momentum theorem to the ball,
Where,
From equation
Substituting the expression for
Substituting
Conclusion:
The angular speed of the ball just after the blow is
(b)
The speed of the ball once it begins to roll without slipping.
(b)
Answer to Problem 106P
Explanation of Solution
Given: Speed of the ball just after the blow is
The coefficient of kinetic friction between the ball and billiard table is
Formula Used:
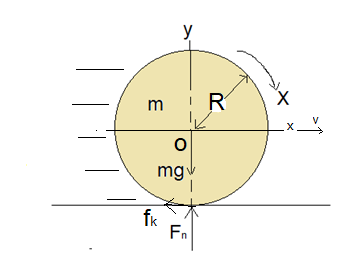
FIGURE: 2
Referring to the force diagram shown in figure 2, applying Newton’s second law to the ball when it is rolling without slipping,
And
Where,
But,
Where,
Calculations:
From equation
Substituting this in equation
From equation
Moment of inertia with respect to an axis through the center of mass of the ball is
Substituting for
Now let us write constant-acceleration equation that connects angular speed of the ball to the angular acceleration and time,
Now,substituting the expression for
Constant acceleration equation that relates the speed of the ball to the acceleration and time,
Where,
Substituting for
Imposing the condition for rolling the ball without slipping,
Substituting this
Conclusion:
The speed of the ball once it begins to roll without slipping is
(c)
The kinetic energy of the ball just after the hit.
(c)
Answer to Problem 106P
Explanation of Solution
Given: The horizontal force applied on a billiard ball at a distance
Speed of the ball just after the blow is
The coefficient of kinetic friction between the ball and billiard table is
Formula Used:
Initial kinetic energy of the ball can be written as,
Where,
Substituting the expressions for
Where,
Moment of inertia,
Substituting these in equation
Conclusion:
The kinetic energy of the ball just after the hit is
Want to see more full solutions like this?
Chapter 9 Solutions
PHYSICS F/SCI.+ENGRS.,STAND.-W/ACCESS
- A long, straight wire carries a current of 10 A along what we’ll define to the be x-axis. A square loopin the x-y plane with side length 0.1 m is placed near the wire such that its closest side is parallel tothe wire and 0.05 m away.• Calculate the magnetic flux through the loop using Ampere’s law.arrow_forwardDescribe the motion of a charged particle entering a uniform magnetic field at an angle to the fieldlines. Include a diagram showing the velocity vector, magnetic field lines, and the path of the particle.arrow_forwardDiscuss the differences between the Biot-Savart law and Coulomb’s law in terms of their applicationsand the physical quantities they describe.arrow_forward
- Explain why Ampere’s law can be used to find the magnetic field inside a solenoid but not outside.arrow_forward3. An Atwood machine consists of two masses, mA and m B, which are connected by an inelastic cord of negligible mass that passes over a pulley. If the pulley has radius RO and moment of inertia I about its axle, determine the acceleration of the masses mA and m B, and compare to the situation where the moment of inertia of the pulley is ignored. Ignore friction at the axle O. Use angular momentum and torque in this solutionarrow_forwardA 0.850-m-long metal bar is pulled to the right at a steady 5.0 m/s perpendicular to a uniform, 0.650-T magnetic field. The bar rides on parallel metal rails connected through a 25-Ω, resistor (Figure 1), so the apparatus makes a complete circuit. Ignore the resistance of the bar and the rails. Please explain how to find the direction of the induced current.arrow_forward
- For each of the actions depicted, determine the direction (right, left, or zero) of the current induced to flow through the resistor in the circuit containing the secondary coil. The coils are wrapped around a plastic core. Immediately after the switch is closed, as shown in the figure, (Figure 1) in which direction does the current flow through the resistor? If the switch is then opened, as shown in the figure, in which direction does the current flow through the resistor? I have the answers to the question, but would like to understand the logic behind the answers. Please show steps.arrow_forwardWhen violet light of wavelength 415 nm falls on a single slit, it creates a central diffraction peak that is 8.60 cm wide on a screen that is 2.80 m away. Part A How wide is the slit? ΟΙ ΑΣΦ ? D= 2.7.10-8 Submit Previous Answers Request Answer × Incorrect; Try Again; 8 attempts remaining marrow_forwardTwo complex values are z1=8 + 8i, z2=15 + 7 i. z1∗ and z2∗ are the complex conjugate values. Any complex value can be expessed in the form of a+bi=reiθ. Find θ for (z1-z∗2)/z1+z2∗. Find r and θ for (z1−z2∗)z1z2∗ Please show all stepsarrow_forward
- Calculate the center of mass of the hollow cone shown below. Clearly specify the origin and the coordinate system you are using. Z r Y h Xarrow_forward12. If all three collisions in the figure below are totally inelastic, which will cause more damage? (think about which collision has a larger amount of kinetic energy dissipated/lost to the environment? I m II III A. I B. II C. III m m v brick wall ע ע 0.5v 2v 0.5m D. I and II E. II and III F. I and III G. I, II and III (all of them) 2marrow_forwardCan you solve this 2 question teach me step by step and draw for mearrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





