Chapter 8.1, Problem 96E

a.

To determine

Use a system of equations to find the equation of the parabola $y=a{x}^2+bx+c$ that passes through the three points. Solve the system using matrices.

Answer to Problem 96E

  $\boxed{y=-0.004x^2+0.367x+5}$

Explanation of Solution

Given information:

A video of the path of a ball thrown by a baseball player was analyzed with a grid covering the TV screen. The video was paused three times, and the position of the ball was measured each time. The coordinates obtained are shown in the table. ( $x$ and $y$ are measured in feet.)

  

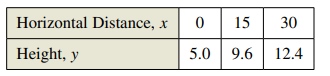
Calculation:

The given form of equation of parabola is,

  $y=a{x}^2+bx+c$

Parabola passes through the points $\left(0,5.0\right)$

  $\begin{array}{l}y=a{x}^2+bx+c\\ 5=a{\left(0\right)}^2+b\left(0\right)+c\\ c=\mathrm{5....}\left(1\right)\end{array}$

Now parabola passes through the points $\left(15,9.6\right)$

  $\begin{array}{l}y=a{x}^2+bx+c\\ 9.6=a{\left(15\right)}^2+b\left(15\right)+c\\ 225a+15b+c=\mathrm{9.6....}\left(2\right)\end{array}$

When parabola passes through the points $\left(30,12.4\right)$

  $\begin{array}{l}y=a{x}^2+bx+c\\ 12.4=a{\left(30\right)}^2+b\left(30\right)+c\\ 900a+30b+c=\mathrm{12.4....}\left(3\right)\end{array}$

Now equation $\left(1\right),\left(2\right),\left(3\right)$ form as system of equation now we solve this system of equations by forming augmented matrix.

  $\left[\begin{array}{ccccc}0& 0& 1& ⋮& 5\\ 225& 15& 1& ⋮& 9.6\\ 900& 30& 1& ⋮& 12.4\end{array}\right]$

Now use graphing calculator to write the matrix in reduced row-echelon form and we get the reduced row-echelon matrix,

  $\begin{array}{l}\left[\begin{array}{ccccc}1& 0& 0& ⋮& -0.004\\ 0& 1& 0& ⋮& 0.367\\ 0& 0& 1& ⋮& 5\end{array}\right]\\ a=-0.004,b=0.367,c=5\end{array}$

Hence, the equation of parabola is, $\boxed{y=-0.004x^2+0.367x+5}$

b.

To determine

Use a graphing utility to graph the parabola.

Answer to Problem 96E

  

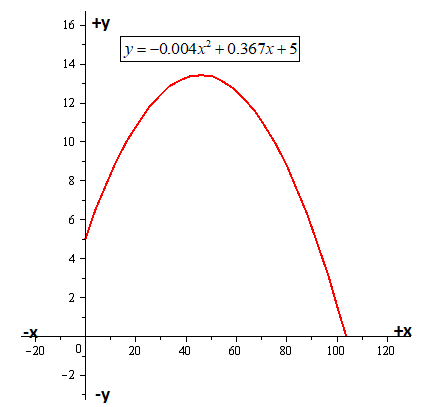
Explanation of Solution

Given information:

A video of the path of a ball thrown by a baseball player was analyzed with a grid covering the TV screen. The video was paused three times, and the position of the ball was measured each time. The coordinates obtained are shown in the table. ( $x$ and $y$ are measured in feet.)

  

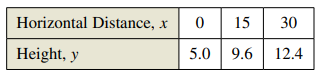
Calculation:

The graph of the parabola is as shown,

  

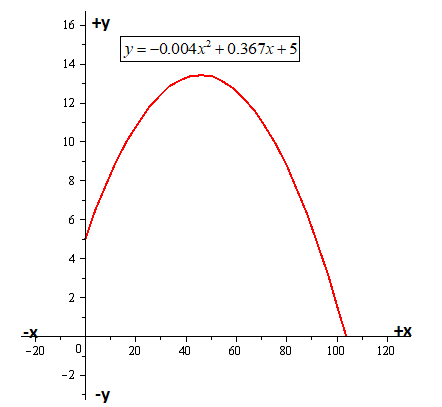
Hence, the graph of parabola is plotted.

c.

To determine

Graphically approximate the maximum height of the ball and the point at which the ball struck the ground.

Answer to Problem 96E

  $\boxed{13.5ft}$

  $\boxed{104ft}$

Explanation of Solution

Given information:

A video of the path of a ball thrown by a baseball player was analyzed with a grid covering the TV screen. The video was paused three times, and the position of the ball was measured each time. The coordinates obtained are shown in the table. ( $x$ and $y$ are measured in feet.)

  

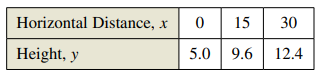
Calculation:

According to the graph the maximum height of the ball is $\boxed{13.5ft}$

The point at which the ball struck the ground is $\boxed{104ft}$

d.

To determine

Analytically find the maximum height of the ball and the point at which the ball struck the ground.

Answer to Problem 96E

  $\boxed{13.418ft}$ , $\boxed{103.793ft}$

Explanation of Solution

Given information:

A video of the path of a ball thrown by a baseball player was analyzed with a grid covering the TV screen. The video was paused three times, and the position of the ball was measured each time. The coordinates obtained are shown in the table. ( $x$ and $y$ are measured in feet.)

  

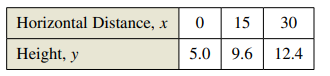
Calculation:

Consider the equation of parabola

  $y=-0.004x^2+0.367x+5$

Now calculate the maximum height of the ball with calculus theory,

For a function $y=f\left(x\right)$ if $y$ is maximum at point $x=c$ ,then we have $f\text{'}\left(c\right)=0$

Now we have,

  $\begin{array}{l}\frac{d}{dx}\left(-0.004x^2+0.367x+5\right)=0\\ -0.004\left(2x\right)+0.367=0\\ x=\frac{0.367}{0.008}\\ x=45.875\end{array}$

Now the maximum height is put $x=45.875$ we get,

  $\begin{array}{l}y=-0.004{\left(45.875\right)}^2+0.367\left(45.875\right)+5\\ =-8.418+16.836+5\\ =13.418ft\end{array}$

  $\boxed{13.418ft}$

Now the point at which the ball struck the ground is,

  $\begin{array}{l}=-0.004x^2+0.367x+5\\ x=103.793ft\end{array}$

Hence, calculated results are $\boxed{13.418ft}$ , $\boxed{103.793ft}$

e.

To determine

Compare your results from parts (c) and (d).

Answer to Problem 96E

Both results are similar.

Explanation of Solution

Given information:

A video of the path of a ball thrown by a baseball player was analyzed with a grid covering the TV screen. The video was paused three times, and the position of the ball was measured each time. The coordinates obtained are shown in the table. ( $x$ and $y$ are measured in feet.)

  

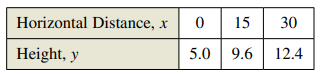
Calculation:

The result from graphically and analytically method, both are similar.

Hence, both results are similar.