10th Edition

ISBN: 9781118230725

Author: David Halliday, Robert Resnick, Jearl Walker

Publisher: Wiley, John & Sons, Incorporated

Concept explainers

Kinetic friction comes into existence when there are moving surfaces means in other words we can say that the force which comes into existing between moving surfaces is known as kinetic friction.

Videos

Textbook Question

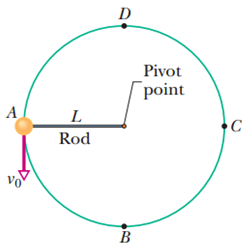
Chapter 8, Problem 87P

SSM A massless rigid rod of length L has a ball of mass m attached to one end (Fig. 8-68). The other end is pivoted in such a way that the ball will move in a vertical circle. First, assume that there is no friction at the pivot. The system is launched downward from the horizontal position A with initial speed v₀. The ball just barely reaches point D and then stops. (a) Derive an expression for v₀ in terms of L, m, and g. (b) What is the tension in the rod when the ball passes through B? (c) A little grit is placed on the pivot to increase the friction there. Then the ball just barely reaches C when launched from A with the same speed as before. What is the decrease in the mechanical energy during this motion? (d) What is the decrease in the mechanical energy by the time the ball finally comes to rest at B after several oscillations?

Chapter 8, Problem 87P, SSM A massless rigid rod of length L has a ball of mass m attached to one end Fig. 8-68. The other

Figure 8-68 Problem 87.

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 8, Problem 86P

Chapter 8, Problem 88P

Students have asked these similar questions

19:39 · C Chegg 1 69% ✓ The compound beam is fixed at Ę and supported by rollers at A and B. There are pins at C and D. Take F=1700 lb. (Figure 1) Figure 800 lb ||-5- F 600 lb بتا D E C BO 10 ft 5 ft 4 ft-—— 6 ft — 5 ft- Solved Part A The compound beam is fixed at E and... Hình ảnh có thể có bản quyền. Tìm hiểu thêm Problem A-12 % Chia sẻ kip 800 lb Truy cập ) D Lưu of C 600 lb |-sa+ 10ft 5ft 4ft6ft D E 5 ft- Trying Cheaa Những kết quả này có hữu ích không? There are pins at C and D To F-1200 Egue!) Chegg Solved The compound b... Có Không ☑ ||| Chegg 10 וח

No chatgpt pls will upvote

Chapter 8 Solutions

Fundamentals of Physics Extended

Ch. 8 - In Fig. 8-18, a horizontally moving block can take...Ch. 8 - Figure 8-19 gives the potential energy function of...Ch. 8 - Figure 8-20 shows one direct path and four...Ch. 8 - In Fig. 8-21, a small, initially stationary block...Ch. 8 - In Fig. 8-22, a block slides from A to C along a...Ch. 8 - In Fig. 8-23a, you pull upward on a rope that is...Ch. 8 - The arrangement shown in Fig. 8-24 is similar to...Ch. 8 - In Fig. 8-25, a block slides along a track that...Ch. 8 - Figure 8-26 shows three situations involving a...Ch. 8 - Figure 8-27 shows three plums that are launched...

Ch. 8 - When a particle moves from f to i and from j to i...Ch. 8 - SSM What is the spring constant of a spring that...Ch. 8 - In Fig. 8-29, a single frictionless roller-coaster...Ch. 8 - You drop a 2.00 kg book to a friend who stands on...Ch. 8 - Figure 8-31 shows a ball with mass m = 0.341 kg...Ch. 8 - SSM In Fig. 8-32, a 2.00 g ice flake is released...Ch. 8 - In Fig. 8-33, a small block of mass m = 0.032 kg...Ch. 8 - Figure 8-34 shows a thin rod, of length L = 2.00 m...Ch. 8 - A 1.50 kg snowball is fired from a cliff 12.5 m...Ch. 8 - GO In Problem 2, what is the speed of the car at a...Ch. 8 - a In Problem 3, what is the speed of the book when...Ch. 8 - SSM WWW a In Problem 5, what is the speed of the...Ch. 8 - a In Problem 8, using energy techniques rather...Ch. 8 - SSM A 5.0 g marble is fired vertically upward...Ch. 8 - a In Problem 4, what initial speed must be given...Ch. 8 - SSM In Fig. 8-35, a runaway truck with failed...Ch. 8 - A 700 g block is released from rest at height h0...Ch. 8 - In Problem 6, what are the magnitudes of a the...Ch. 8 - a In Problem 7, what is the speed of the ball at...Ch. 8 - GO Figure 8-36 shows an 8.00 kg stone at rest on a...Ch. 8 - GO A pendulum consists of a 2.0 kg stone swinging...Ch. 8 - Figure 8-34 shows a pendulum of length L = 1.25 m....Ch. 8 - A 60 kg skier starts from rest at height H = 20 m...Ch. 8 - ILW The string in Fig. 8-38 is L = 120 cm long,...Ch. 8 - A block of mass m = 2.0 kg is dropped from height...Ch. 8 - At t = 0 a 1.0 kg ball is thrown from a tall tower...Ch. 8 - A conservative force F=(6.0x12)i N, where x is in...Ch. 8 - Tarzan, who weighs 688 N, swings from a cliff at...Ch. 8 - Figure 8-41a applies to the spring in a cork gun...Ch. 8 - SSM WWW In Fig. 8-42, a block of mass m = 12 kg is...Ch. 8 - GO A 2.0 kg breadbox on a frictionless incline of...Ch. 8 - ILW A block with mass m = 2.00 kg is placed...Ch. 8 - In Fig. 8-45, a chain is held on a frictionless...Ch. 8 - GO In Fig. 8-46, a spring with k = 170 N/m is at...Ch. 8 - GO A boy is initially seated on the top of a...Ch. 8 - GO In Fig. 8-42, a block of mass m = 3.20 kg...Ch. 8 - GO Two children are playing a game in which they...Ch. 8 - A uniform cord of length 25 cm and mass 15 g is...Ch. 8 - Figure 8-49 shows a plot of potential energy U...Ch. 8 - GO Figure 8-50 shows a plot of potential energy U...Ch. 8 - The potential energy of a diatomic molecule a...Ch. 8 - A single conservative force Fx acts on a 1.0 kg...Ch. 8 - A worker pushed a 27 kg block 9.2 m along a level...Ch. 8 - A collie drags its bed box across a floor by...Ch. 8 - A horizontal force of magnitude 35.0 N pushes a...Ch. 8 - SSM A rope is used to pull a 3.57 kg block at...Ch. 8 - An outfielder throws a baseball with an initial...Ch. 8 - A 75 g Frisbee is thrown from a point 1.1 m above...Ch. 8 - In Fig. 8-51, a block slides down an incline. As...Ch. 8 - SSM ILW A 25 kg bear slides, from rest, 12 m down...Ch. 8 - A 60 kg skier leaves the end of a ski-jump ramp...Ch. 8 - During a rockslide, a 520 kg rock slides from rest...Ch. 8 - A large fake cookie sliding on a horizontal...Ch. 8 - GO In Fig. 8-52, a 3.5 kg block is accelerated...Ch. 8 - A child whose weight is 267 N slides down a 6.1 m...Ch. 8 - ILW In Fig. 8-53, a block of mass m = 2.5 kg...Ch. 8 - You push a 2.0 kg block against a horizontal...Ch. 8 - GO In Fig. 8-54, a block slides along a track from...Ch. 8 - A cookie jar is moving up a 40 incline. At a point...Ch. 8 - A stone with a weight of 5.29 N is launched...Ch. 8 - Prob. 60P Ch. 8 - When a click beetle is upside down on its back, it...Ch. 8 - GO In Fig. 8-55, a block slides along a path that...Ch. 8 - The cable of the 1800 kg elevator cab in Fig. 8-56...Ch. 8 - GO In Fig. 8-57, a block is released from rest at...Ch. 8 - GO A particle can slide along a track with...Ch. 8 - A 3.2 kg sloth hangs 3.0 m above the ground. a...Ch. 8 - SSM A spring k = 200 N/m is fixed at the top of a...Ch. 8 - From the edge of a cliff, a 0.55 kg projectile is...Ch. 8 - SSM In Fig. 8-60, the pulley has negligible mass,...Ch. 8 - GO In Fig. 8-38, the string is L = 120 cm long,...Ch. 8 - SSM In Fig. 8-51, a block is sent sliding down a...Ch. 8 - Two snowy peaks are at heights H = 850 m and h =...Ch. 8 - SSM The temperature of a plastic cube is monitored...Ch. 8 - A skier weighing 600 N goes over a frictionless...Ch. 8 - SSM To form a pendulum, a 0.092 kg ball is...Ch. 8 - We move a particle along an x axis, first outward...Ch. 8 - SSM A conservative force Fx acts on a 2.00 kg...Ch. 8 - At a certain factory, 300 kg crates are dropped...Ch. 8 - SSM A 1500 kg car begins sliding down a 5.0...Ch. 8 - In Fig. 8-65, a 1400 kg block of granite is pulled...Ch. 8 - A particle can move along only an x axis, where...Ch. 8 - For the arrangement of forces in Problem 81, a...Ch. 8 - SSM A 15 kg block is accelerated at 2.0 m/s2 along...Ch. 8 - A certain spring is found not to conform to Hookes...Ch. 8 - SSM Each second, 1200 m3 of water passes over a...Ch. 8 - GO In Fig. 8-67, a small block is sent through...Ch. 8 - SSM A massless rigid rod of length L has a ball of...Ch. 8 - A 1.50 kg water balloon is shot straight up with...Ch. 8 - A 2.50 kg beverage can is thrown directly downward...Ch. 8 - A constant horizontal force moves a 50 kg trunk...Ch. 8 - GO Two blocks, of masses M = 2.0 kg and 2M, are...Ch. 8 - A volcanic ash flow is moving across horizontal...Ch. 8 - A playground slide is in the form of an arc of a...Ch. 8 - The luxury liner Queen Elizabeth 2 has a...Ch. 8 - A factory worker accidentally releases a 180 kg...Ch. 8 - If a 70 kg baseball player steals home by sliding...Ch. 8 - A 0.50 kg banana is thrown directly upward with an...Ch. 8 - A metal tool is sharpened by being held against...Ch. 8 - A swimmer moves through the water at an average...Ch. 8 - An automobile with passengers has weight 16 400 N...Ch. 8 - A 0.63 kg ball thrown directly upward with an...Ch. 8 - The summit of Mount Everest is 8850 m above sea...Ch. 8 - A sprinter who weighs 670 N runs the first 7.0 m...Ch. 8 - A 20 kg object is acted on by a conservative force...Ch. 8 - A machine pulls a 40 kg trunk 2.0 m up a 40 ramp...Ch. 8 - Prob. 106P Ch. 8 - The only force acting on a particle is...Ch. 8 - In 1981, Daniel Goodwin climbed 443 m up the...Ch. 8 - A 60.0 kg circus performer slides 4.00 m down a...Ch. 8 - A 5.0 kg block is projected at 5.0 m/s up a plane...Ch. 8 - A 9.40 kg projectile is fired vertically upward....Ch. 8 - A 70.0 kg man jumping from a window lands in an...Ch. 8 - A 30 g bullet moving a horizontal velocity of 500...Ch. 8 - A 1500 kg car starts from rest on a horizontal...Ch. 8 - A 1.50 kg snowball is shot upward at an angle of...Ch. 8 - A 68 kg sky diver falls at a constant terminal...Ch. 8 - A 20 kg block on a horizontal surface is attached...Ch. 8 - Resistance to the motion of an automobile consists...Ch. 8 - SSM A 50 g ball is thrown from a window with an...Ch. 8 - A spring with a spring constant of 3200 N/m is...Ch. 8 - A locomotive with a power capability of 1.5 MW can...Ch. 8 - SSM A 0.42 kg shuffleboard disk is initially at...Ch. 8 - A river descends 15 m through rapids. The speed of...Ch. 8 - The magnitude of the gravitational force between a...Ch. 8 - Approximately 5.5 106 kg of water falls 50 m over...Ch. 8 - To make a pendulum, a 300 g ball is attached to...Ch. 8 - In a circus act, a 60 kg clown is shot from a...Ch. 8 - A 70 kg firefighter slides, from rest, 4.3 m down...Ch. 8 - The surface of the continental United States has...Ch. 8 - A spring with spring constant k = 200 N/m is...Ch. 8 - Fasten one end of a vertical spring to a ceiling,...Ch. 8 - The maximum force you can exert on an object with...Ch. 8 - Conservative force Fx acts on a particle that...Ch. 8 - Figure 8-73a shows a molecule consisting of two...Ch. 8 - Repeat Problem 83, but now with the block...Ch. 8 - A spring with spring constant k = 620 N/m is...

Additional Science Textbook Solutions

Find more solutions based on key concepts

If all of Earths nitrogen-fixing prokaryotes were to die suddenly, what would happen to the concentration of ni...

Biology: Life on Earth with Physiology (11th Edition)

What is the contour interval of this map?

Applications and Investigations in Earth Science (9th Edition)

3. What is free-fall, and why does it make you weightless? Briefly describe why astronauts are weightless in th...

The Cosmic Perspective (8th Edition)

75. A Ford Mustang can accelerate from 0 to 60 mph in a time of 5.6 s. A Mini Cooper isn’t capable of such a ra...

College Physics: A Strategic Approach (3rd Edition)

Which culture uses NAD+? Use the following choices to answer questions. a. E. coli growing in glucose broth at ...

Microbiology: An Introduction

Choose the best answer to etch of the following. Explain your reasoning. Which of these stars has the largest r...

Cosmic Perspective Fundamentals

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.