
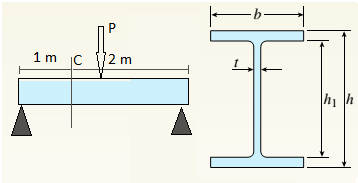
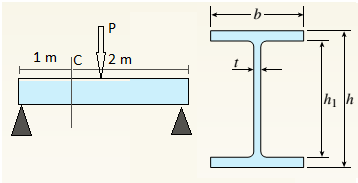
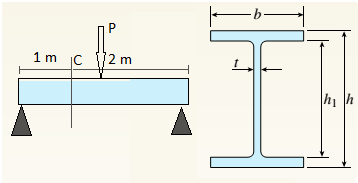
A beam with a wide-flange cross section (see figure) has the following dimensions: h = 120 mm, r = 10 mm, h = 300 mm, and /ij = 260 mm. The beam is simply supported with span length L = 3,0 im A concentrated load P = 120 kN acts at the midpoint of the span.
At across section located 1.0 m from the left-hand support, determine the principal stresses tr, and tr2and the maximum shear stress Tmax at each of the following locations: (a) the top of the beam, (b) the top of the web, and (c) the neutral axis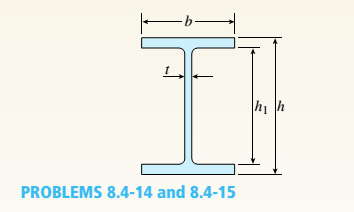
(a).
Find principal stresses and maximum shear stress at top of beam.
Answer to Problem 8.4.14P
Principal stresses
Maximum shear stress
Explanation of Solution
Given Information:
Beam length
Point load
Concept Used:
Bending stress
Shear stress
Principal normal stresses
Maximum shear stress
So bending moment at point
Shear force at point
Moment of inertia,
First moment of area at the top of beam shall be zero,
So bending stress at top,
And shear stress at that point,
For this situation no stress in
Principal normal stresses are given by following equation,
Maximum shear stress,
Conclusion:
Hence we get,
Principal stresses
Maximum shear stress
(b).
Find principal stresses and maximum shear stress at top of web.
Answer to Problem 8.4.14P
Principal stresses
Maximum shear stress
Explanation of Solution
Given Information:
Beam length
Point load
Concept Used:
Bending stress
Shear stress
Principal normal stresses
Maximum shear stress
So bending moment at point
Shear force at point
Moment of inertia,
First moment of area of flange,
So bending stress at top of web,
And shear stress at that point,
For this situation no stress in
Principal normal stresses are given by following equation,
Maximum shear stress,
Conclusion:
Hence we get,
Principal stresses
Maximum shear stress
(c).
Find principal stresses and maximum shear stress at neutral axis.
Answer to Problem 8.4.14P
Principal stresses
Maximum shear stress
Explanation of Solution
Given Information:
Beam length
Point load
Concept Used:
Bending stress
Shear stress
Principal normal stresses
Maximum shear stress
So bending moment at point
Shear force at point
Moment of inertia,
First moment of area for the section above the neutral axis,
So bending stress at neutral axis,
And shear stress at that point,
For this situation no stress in
Principal normal stresses are given by following equation,
Maximum shear stress,
Conclusion:
Hence we get,
Principal stresses
Maximum shear stress
Want to see more full solutions like this?
Chapter 8 Solutions
Mechanics of Materials (MindTap Course List)
- Solve this problem and show all of the workarrow_forwardSolve this problem and show all of the workarrow_forwardPart A The man pulls on the rope with a force of F = 30 N as shown in (Figure 1). Figure 1.5 m 3 m. 4m 10.5 m 1 of 1 Determine the position vector from O to A. Express the x, y, and z components of the position vector in meters to three significant figures separated by commas. ΜΕ ΑΣΦ vec (TOA). (TOA)y. (TOA)== Submit Request Answer Part B m Determine the position vector from O to B. Express the x, y, and z components of the position vector in meters to three significant figures separated by commas. ΜΕ ΑΣΦ ↓↑ vec (TOB)x, (TOB)y, (TOB) = Submit Request Answer Part C Complete previous part(s) Provide Feedback ? marrow_forward
- 4 Part A The tool is used to shut off gas valves that are difficult to access (Figure 1). Figure 0.25 m 30 0,4 m < 1 of 1 If the force F= {-60i+40j+15k} N is applied to the handle, determine the component of the moment created about the z axis of the valve. Express your answer with the appropriate units. Mz = Value Submit Request Answer Provide Feedback | ? Unitsarrow_forward3. A steam power plant has an average monthly net power delivery of 740 MW over the course of a year. This power delivery is accomplished by burning coal in the boiler. The coal has a heating value of 9150 Btu/lbm. The cost of the coal is $14.20/ton. The overall thermal efficiency of the plant is, nth Wnet Qboiler 0.26 = 26% Determine the annual cost of the coal required to deliver the given average monthly power.arrow_forwardThe cable exerts a force of P = 4 kN at the end of the 8-m-long crane boom. A P 8 m B -x- I'm En ▾ Part A If 0 = 30°, determine the placement x of the boom at B so that this force creates a maximum moment about point O. Express your answer to three significant figures and include the appropriate units. x = 9.81 m Submit Previous Answers ✓ Correct ▾ Part B What is this moment? Express your answer to three significant figures and include the appropriate units. Assume the positive direction is counterclockwise. (Mo) max 43.7 = E ? N Submit Previous Answers Request Answer X Incorrect; Try Again; 28 attempts remaining Enter your answer with a different unit type. Review a list of acceptable units.arrow_forward
- Find highest and lowest temperature.arrow_forwardExplained step by step.arrow_forwardThe bevel gear shown in is subjected to the force F which is caused from contact with another gear. Part A F (201+8j 15k) N 40 mm Determine the moment of this force about the y axis of the gear shaft. Express your answer with the appropriate units. My = Value Submit Request Answer ? Units 30 mmarrow_forward
- Consider the beam in. Part A 1.5 ft 200 lb 200lb 2 ft 30° 1.25 ft 30° If F 90 lb, determine the resultant couple moment. = Express your answer in pound-feet to three significant figures. Assume the positive direction is counterclockwise. ΑΣΦ vec MR = Submit Request Answer ? lb.ftarrow_forward4. An operating parameter often used by power plant engineers is the heat rate. The heat rate is defined as, HR Qbioler Wnet where Qbioler is the heat transfer rate (Btu/h) to the water in the boiler due to the combustion of a fuel and Wnet is the net power (kW) delivered by the plant. In comparison, the thermal efficiency of the power plant is defined as, nth Wnet Qbioler where the numerator and denominator have the same units. Consider a power plant that is delivering 1000 MW of power while utilizing a heat transfer rate of 3570 MW at the boiler. Determine the heat rate and thermal efficiency of this power plant.arrow_forwardThe shaft shown in the sketch is subjected to tensile torsional and bending loads Determine the principal stresses at the location of stress concentration ✓ D=45MR F=3MM 1000-M 1000N チ d=30mm 500N 150 мм MM- 120 MA-arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
