
A W 12 X 14 wide-flange beam (see Table F-l(a), Appendix F) is simply supported with a span length of 120 in. (see figure). The beam supports two anti-symmetrically placed concentrated loads of 7,5 kips each.
At a cross section located 20 in. from the right-hand support, determine the principal stresses (7]and (7\ and the maximum shear stress Tmaw at each of the following locations: (a) the top of the beam, (b) the top of the web, and (c) the neutral axis,
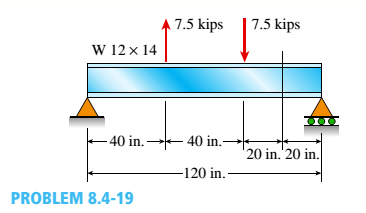
(a).
To find: Values of principal stresses and maximum shear stress at top of beam.
Answer to Problem 8.4.19P
Values of principal stress :
Maximum shear stress
Explanation of Solution
Given Information:
Beam length
Point load
Dimensions of beam,
Concept Used:
Bending stress
Shear stress
Principal normal stresses
Maximum shear stress
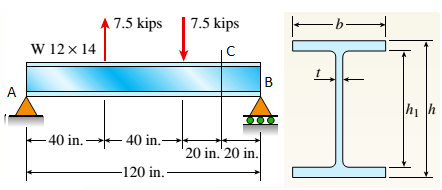
From equilibrium:
So, bending moment at point
Shear force at point
Moment of inertia:
First moment of area at the top of beam shall be zero,
So, bending stress at top:
And shear stress at that point:
For this situation no stress in
Values of normal stress is given by following equation:
Maximum shear stress:
Conclusion:
Hence, we get:
Values of principal stress:
Maximum shear stress
(b).
To find: Values of principal stresses and maximum shear stress at top of web.
Answer to Problem 8.4.19P
Values of principal stress:
Maximum shear stress
Explanation of Solution
Given Information:
Beam length
Point load
Dimensions of beam,
Concept Used:
Bending stress
Shear stress
Principal normal stresses
Maximum shear stress
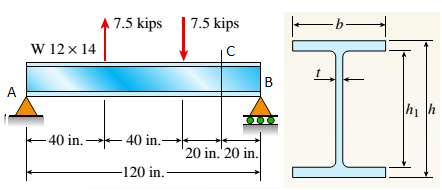
From equilibrium,
So, bending moment at point
Shear force at point
Moment of inertia:
First moment of area of flange:
So, bending stress at top of web:
And shear stress at that point:
For this situation no stress in
Principal normal stresses are given by following equation,
Maximum shear stress,
Conclusion:
Hence we get,
Principal stresses
Maximum shear stress
(c).
Find principal stresses and maximum shear stress at neutral axis.
Answer to Problem 8.4.19P
Principal stresses
Maximum shear stress
Explanation of Solution
Given Information:
Beam length
Point load
Dimensions of beam,
Concept Used:
Bending stress
Shear stress
Principal normal stresses
Maximum shear stress
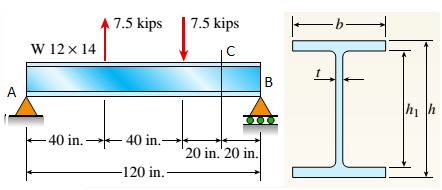
From equilibrium,
So bending moment at point
Shear force at point
Moment of inertia,
First moment of area for the section above the neutral axis,
So bending stress at neutral axis,
And shear stress at that point,
For this situation no stress in
Principal normal stresses are given by following equation,
Maximum shear stress,
Conclusion:
Hence we get,
Principal stresses
Maximum shear stress
Want to see more full solutions like this?
Chapter 8 Solutions
Mechanics of Materials (MindTap Course List)
- Please do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardCE-112 please solve this problem step by step and give me the correct answerarrow_forward
- CE-112 please solve this problem step by step and give me the correct asnwerarrow_forwardthis is an old practice exam, the answer is Ax = -4, Ay = -12,Az = 32.5, Bx= 34, Bz = 5, By = 0 but how?arrow_forwardThis is an old practice exam, the answer is Ax = Az = 0, Ay = 2000, TDE = 4750, Cx = 2000, Cy = 2000, Cz = -800 but how?arrow_forward
- this is an old practice exam, the answer is Fmin = 290.5lb but howarrow_forwardThis is an exam review question. The answer is Pmin = 622.9 lb but whyarrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forward
- Please do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardThis is an old practice exam. Fce = 110lb and FBCD = 62 lb but whyarrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
