
Concept explainers
Draw the influence lines for the force in member AB, BG, DF, and FG.
Explanation of Solution
Calculation:
Find the support reactions.
Apply 1 k moving load from E to G in the top chord member.
Draw the free body diagram of the member as in Figure 1.
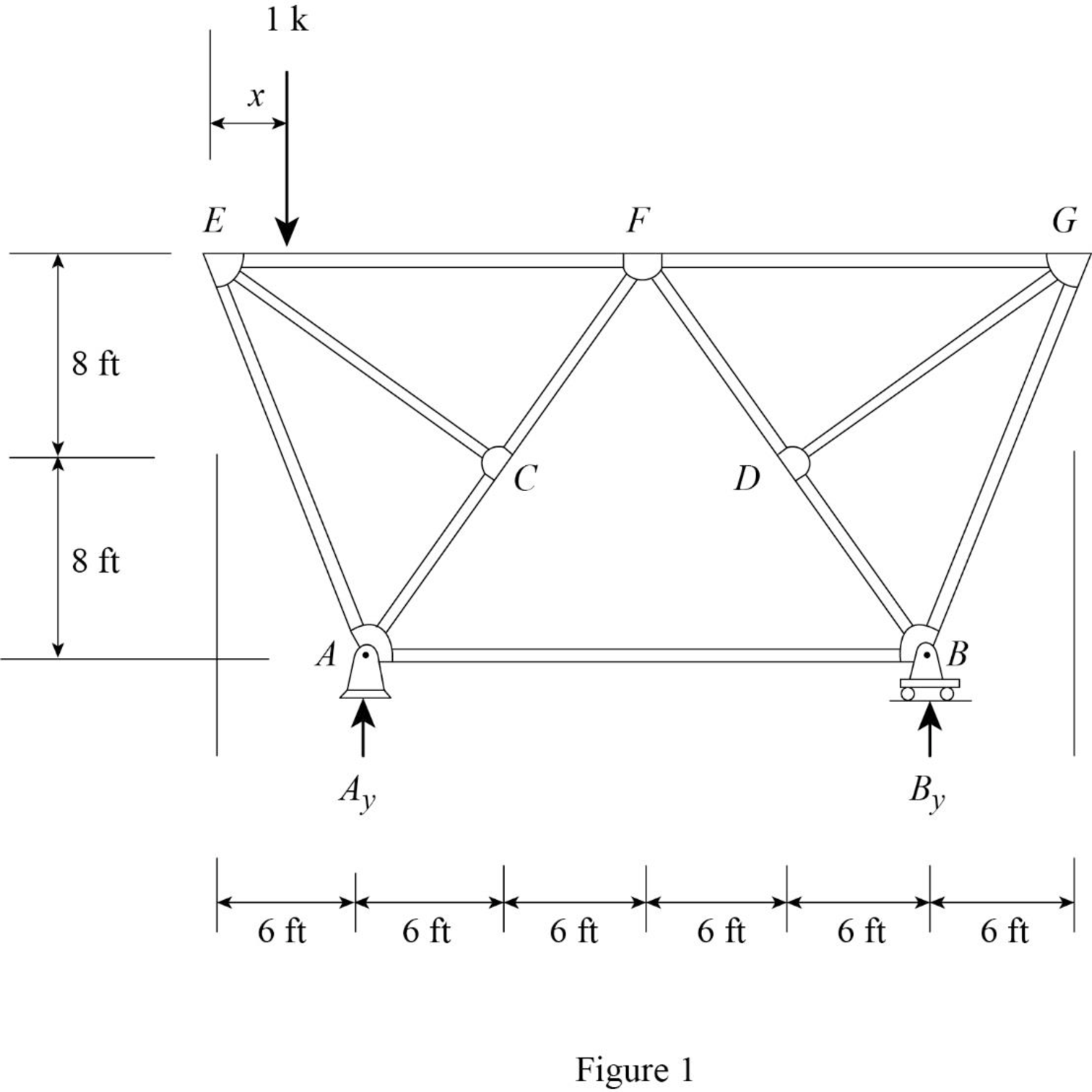
Find the reaction at A and B when 1 k load placed from E to G.
Apply moment equilibrium at A.
Apply force equilibrium equation along vertical.
Consider the upward force as positive
Influence line for the force in member AB.
The expressions for the member force
Draw the free body diagram of member with section aa as shown in Figure 2.
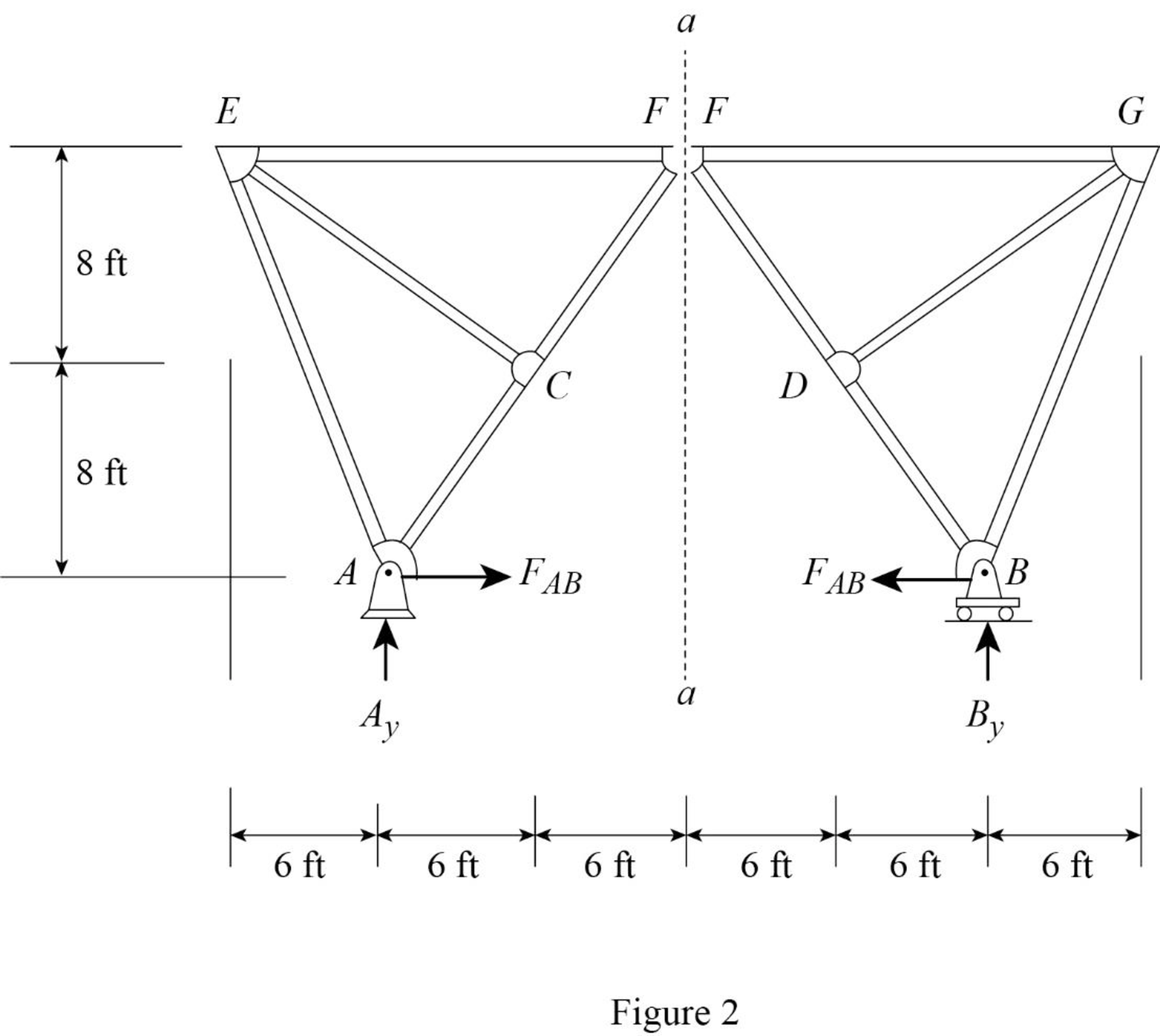
Refer Figure 2.
Find the equation of member force AB.
Apply a 1 k load at just left of F
Consider the right hand portion to section a-a.
Apply moment equilibrium equation at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Apply a 1 k load at just right of F
Consider the left hand portion to section a-a.
Apply moment equilibrium equation at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member AB,
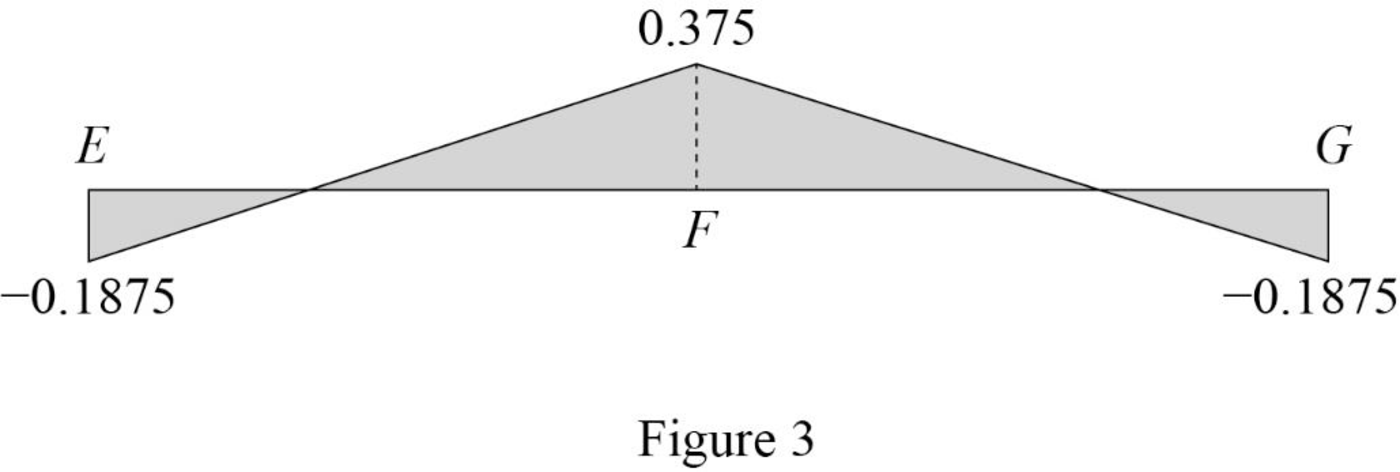
Find the force in member AB using the Equation (1) and (2) and then summarize the value in Table 1.
| x (ft) | Apply 1 k load | Force in member AB (k) | Influence line ordinate for the force in member AB (k/k) |
| 0 | E | ||
| 18 | F | 0.375 | |
| 36 | G |
Sketch the influence line diagram for ordinate for the force in member AB using Table 2 as shown in Figure 3.
Influence line for the force in member BG.
The expressions for the member force
Draw the free body diagram of section a-a as shown in Figure 4.
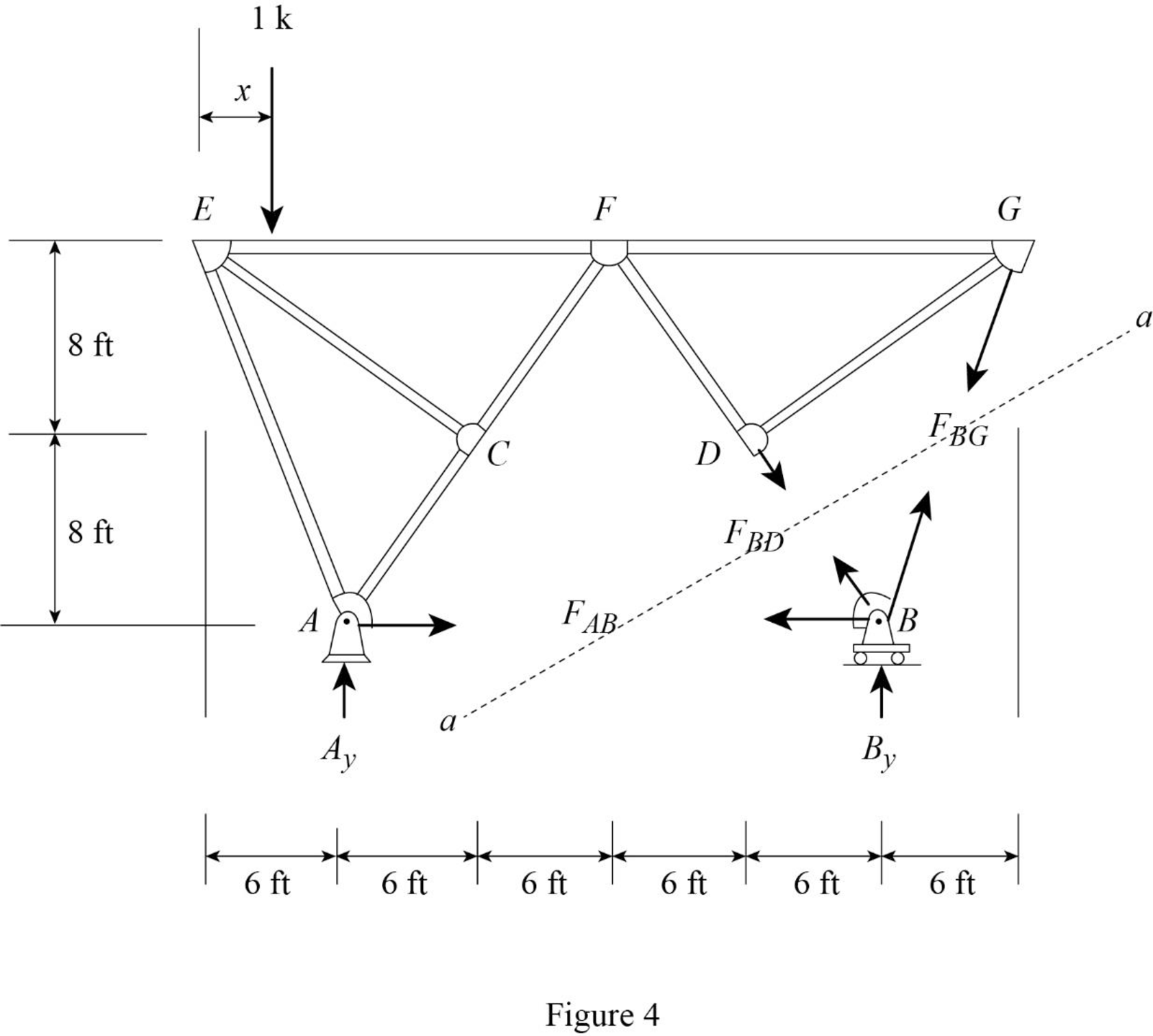
Refer Figure 4.
Find the force in member BG.
Apply 1 k load just left of F
Consider the section EF.
The member force of EF not affected when 1 k load applied from E to F. Therefore, the influence line ordinate of member force BG is 0 k/k from E to F.
Apply a 1 k load just the right of F
Apply moment equilibrium at F.
Consider the section right of line a-a.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member BG,
Find the force in member BG using the Equation (3) and (4) and then summarize the value in Table 2.
| x (ft) | Apply 1 k load | Force in member BG (k) | Influence line ordinate for the force in member BG (k/k) |
| 0 | E | 0 | |
| 18 | F | 0 | |
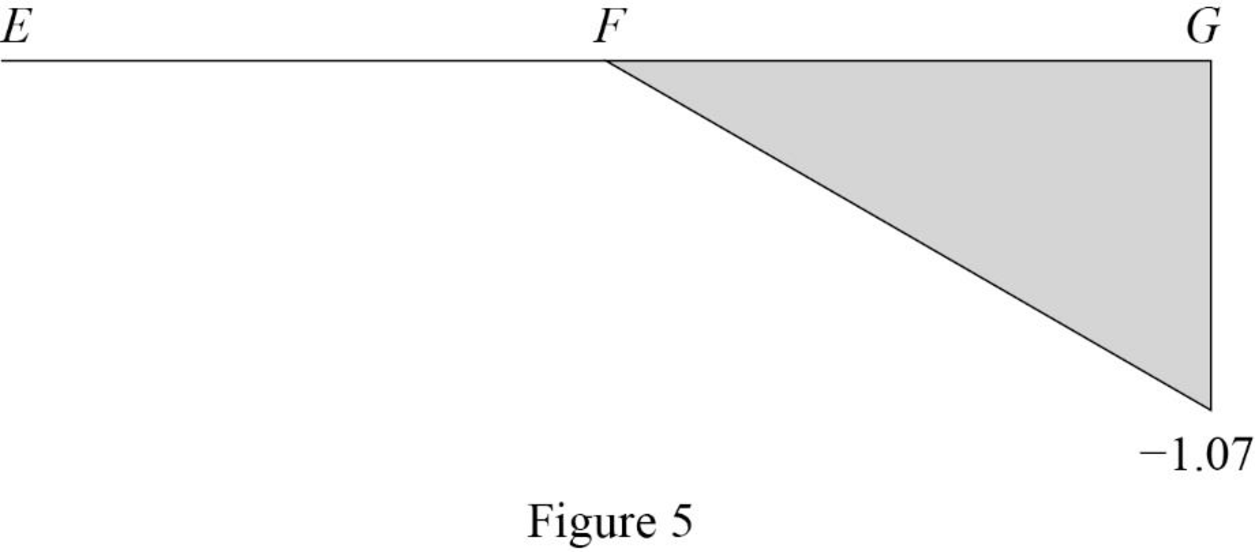
| 36 | G | ‑1.07 |
Sketch the influence line diagram for ordinate for the force in member BG using Table 2 as shown in Figure 5.
Influence line for the force in member DF.
The expressions for the member force
Draw the free body diagram of section a-a as shown in Figure 6.
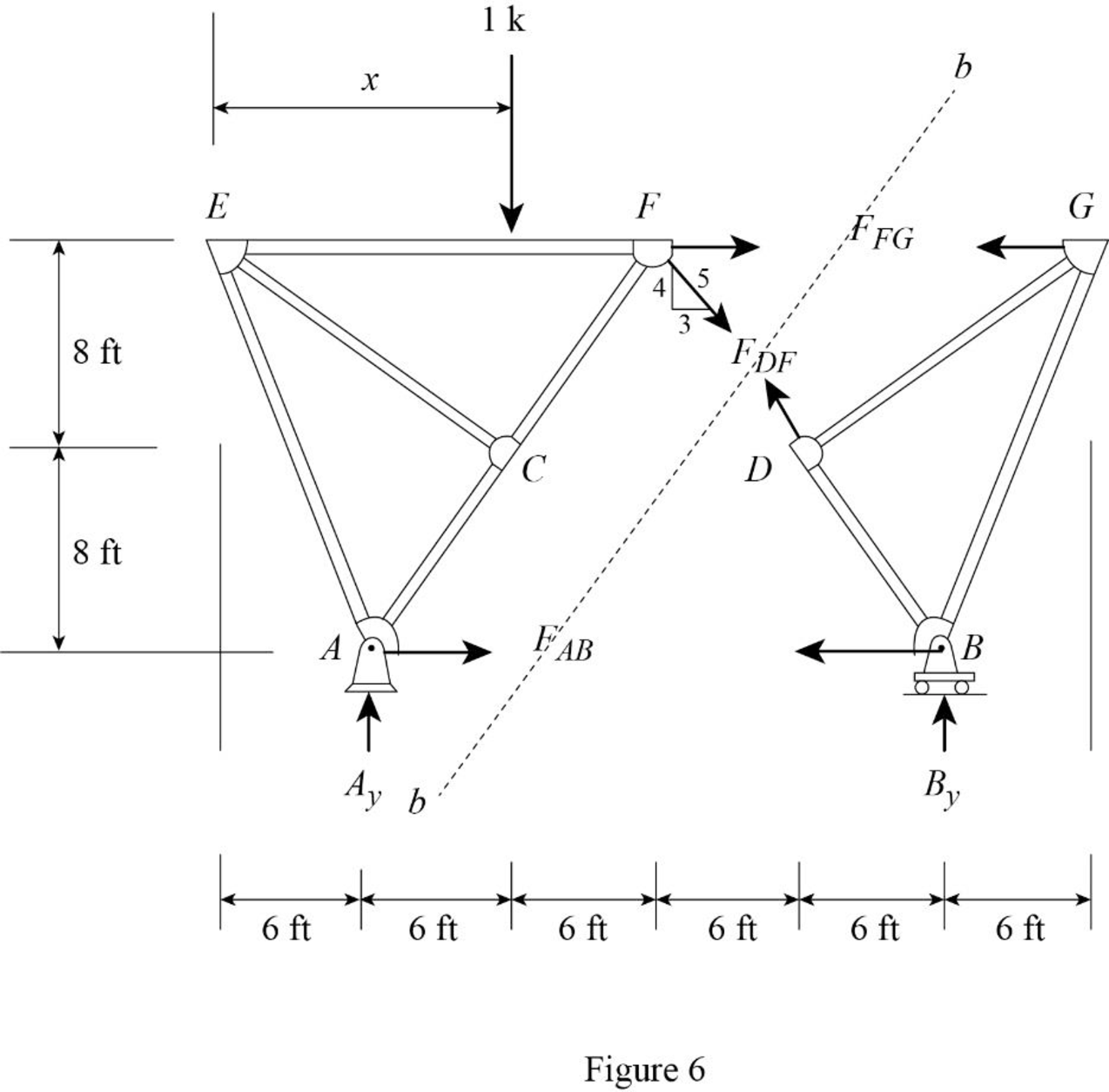
Refer Figure 6.
Find the force in member DF.
Apply 1 k load just left of F
Consider the section right of line bb.
Apply moment equilibrium at G.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Apply 1 k load just right of F
Consider the section left of line bb.
Apply moment equilibrium at E.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member DF,
Find the force in member DF using the Equation (5) and (6) and then summarize the value in Table 3.
| x (ft) | Apply 1 k load | Force in member DF (k) | Influence line ordinate for the force in member DF (k/k) |
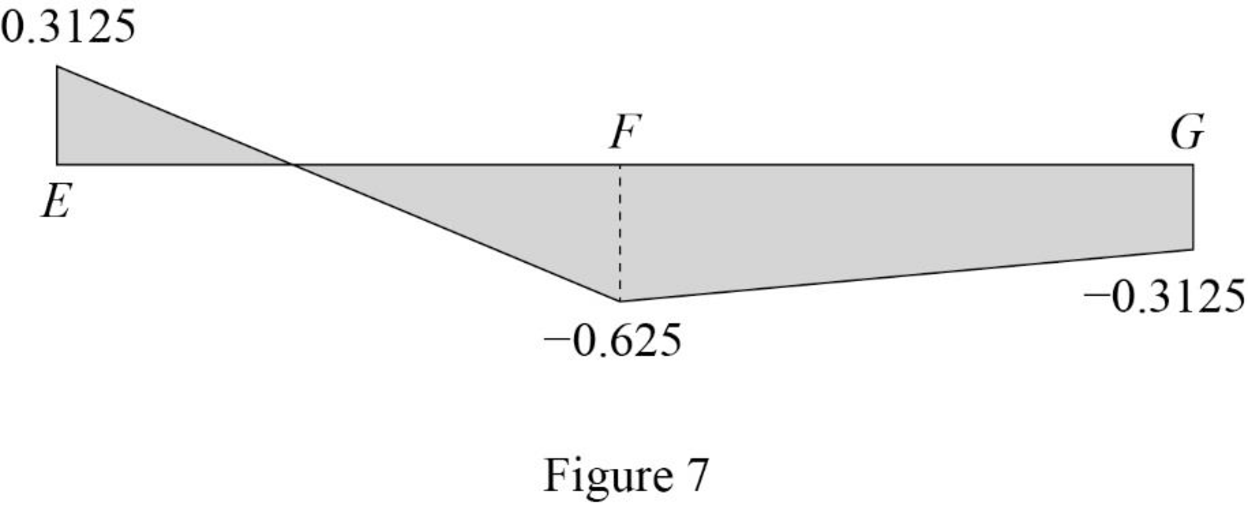
| 0 | E | 0.3125 | |
| 18 | F | ‑0.625 | ‑0.625 |
| 36 | G | ‑0.3125 | ‑0.3125 |
Sketch the influence line diagram for ordinate for the force in member DF using Table 3 as shown in Figure 7.
Influence line for the force in member FG.
Refer Figure 6.
Find the force in member FG.
Apply 1 k load just left of F
Consider the section right of line bb.
Apply moment equilibrium at B.
Consider clockwise moment as positive and anticlockwise moment as negative.
Apply 1 k load just right of F
Consider the section left of line bb.
Apply moment equilibrium at A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member FG,
Find the force in member FG using the Equation (7) and (8) and then summarize the value in Table 4.
| x (ft) | Apply 1 k load | Force in member FG (k) | Influence line ordinate for the force in member FG (k/k) |
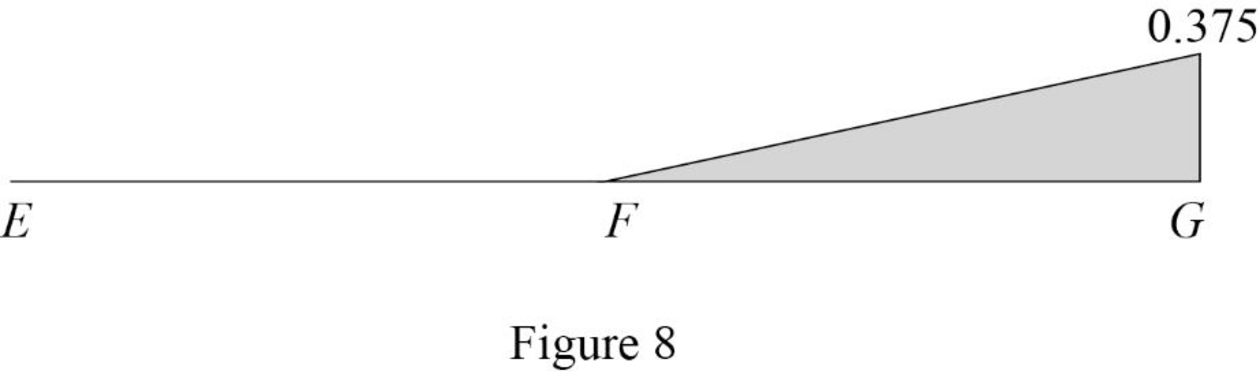
| 0 | E | 0.3125 | |
| 18 | F | ‑0.625 | ‑0.625 |
| 36 | G | ‑0.3125 | ‑0.3125 |
Sketch the influence line diagram for ordinate for the force in member FG using Table 4 as shown in Figure 8.
Want to see more full solutions like this?
Chapter 8 Solutions
Structural Analysis, SI Edition
- Text Book Problem 7.82 (page 261) Consider the total head-loss in the system forthis flow is 18.56 ft (head-losses in first and second pipe are 13.83 ft and 4.73 ftrespectively). Please show numerical values for EGL/HGL at the beginning/end/intermediatechange point. (Point distribution: elevation determination 5 points, EGL, HGL lines 4points).(I think we are just using the values provided for head losses to solve this problem)arrow_forwardCalculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the moment distribution method, and draw the Shear force diagram and Bending moment diagram for the beam shown. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.arrow_forwardCalculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the Slope deflection method. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.arrow_forward
- Thank you for your help if you would also provide the equations used .arrow_forwardThe sectors are divided as follows:top right = 1, top left = 2, middle = 3, bottom = 4.(a) Determine the distance yˉ to the centroid of the beam’s cross-sectional area.Solve the next questions by building a table. (Table format Answers) (b) Determine the second moment of area (moment of inertia) about the x′ axis. (c) Determine the second moment of area (moment of inertia) about the y-axis.arrow_forwardinstructions: make sure to follow the instructions and provide complete and detailed solution create/draw a beam with uniformly distributed load and concentrated load after, find the shear and moment equation and ensure to draw it's shear and moment diagram once done, write it's conclusion or observation 4:57 PMarrow_forward
- Solve for forces on pin C and Darrow_forwardBorrow pit soil is being used to fill an 900,00 yd3 of depression. The properties of borrowpit and in-place fill soils obtained from laboratory test results are as follows:• Borrow pit soil: bulk density 105 pcf, moisture content = 8%, and specific gravity = 2.65• In-place fill soil: dry unit weight =120 pcf, and moisture content = 16%(a) How many yd3 of borrow soil is required?(b) What water mass is needed to achieve 16% moisture in the fill soil?(c) What is the in-place density after a long rain?arrow_forwardsolve for dt/dx=f(t,x)=x+t^2arrow_forward
- Calculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the slope deflection method, draw the resulting shear force diagran and bending moment diagram. The beam is subjected to an UDL of w=65m. L=4.5m, L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200 GPa, I = 250x106 mm4.arrow_forwardProblem 2 (A is fixed and C is a pin) Find the reactions and A and C. 10 k- 6 ft 6 ft B A 2 k/ft 15 ftarrow_forward6. A lake with no outlet is fed by a river with a constant flow of 1200 ft3/s. Water evaporates from the surface at a constant rate of 13 ft3/s per square mile of surface area. The surface area varies with the depth h (in feet) as A (square miles) = 4.5 + 5.5h. What is the equilibrium depth of the lake? Below what river discharge (volume flow rate) will the lake dry up?arrow_forward
