Chapter 8, Problem 21P

To determine

Draw the influence lines for the shear and bending moment at point B.

Draw the influence lines for the shear at internal hinge C.

Explanation of Solution

Calculation:

Influence line for shear at point B:

Apply a 1 kN unit moving load at a distance of x from left end A.

Sketch the free body diagram of frame as shown in Figure 1.

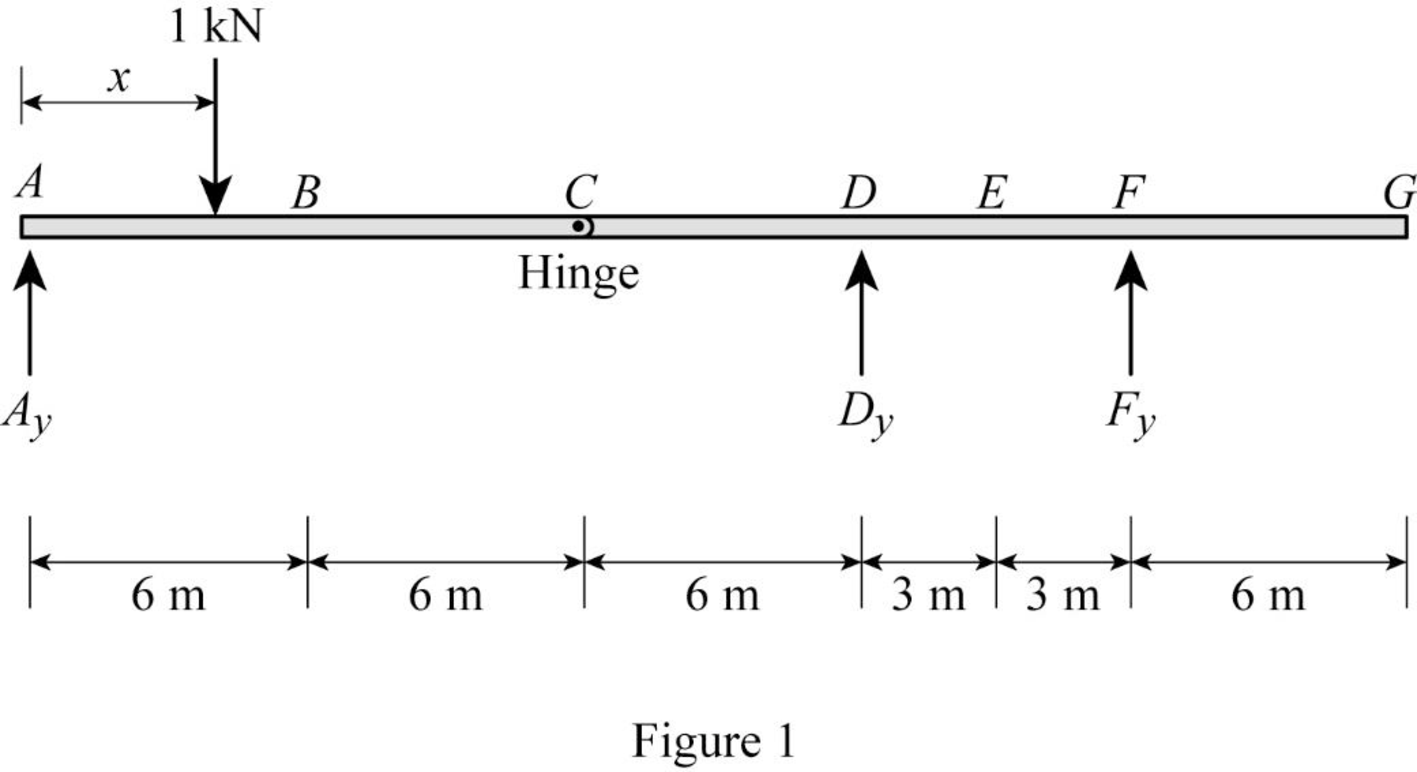
Refer Figure 1.

Consider the unit load at a variable position x to the left hinge C. (placed portion AC of the beam $0\le x<12\text{m}$).

Find the vertical support reaction $\left(A_y\right)$ at A for portion AC.

Take Moment at hinge C from left end A.

Consider clockwise moment as positive and anticlockwise moment as negative.

$\begin{array}{l}\Sigma M_C^{AC}=0\\ A_y\left(12\right)-1\left(12-x\right)=0\\ 12A_y=12-x\\ A_y=1-\frac{x}{12}\end{array}$

Consider the unit load at a variable position x to the right hinge C. (Place portion CG of the beam $12\text{m}<x\le 30\text{m}$).

Find the vertical support reaction $\left(A_y\right)$ at A for portion CG.

Take Moment at hinge C from left end A.

Consider clockwise moment as positive and anticlockwise moment as negative.

$\begin{array}{l}\Sigma M_C^{AC}=0\\ A_y\left(12\right)=0\\ A_y=0\end{array}$

Thus, the equations of the influence line ordinate for $A_y$ are,

$A_y=1-\frac{x}{12},0\le x<12\text{m}$ (1)

$A_y=0,12\text{m}<x\le 30\text{m}$ (2)

Refer Figure 1.

Find the equation of influence line ordinate for the vertical reaction $\left(D_y\right)$ using equilibrium equation.

Apply moment equilibrium at F.

Consider clockwise moment as positive and anticlockwise moment as negative.

$\begin{array}{l}\Sigma M_F=0\\ A_y\left(24\right)+D_y\left(6\right)-1\left(24-x\right)=0\\ 6D_y=24-x-24A_y\\ D_y=4-\frac{x}{6}-4A_y\end{array}$ (3)

Find the influence line ordinate of vertical reaction $\left(D_y\right)$ for portion AC $\left(0\le x<12\text{m}\right)$.

Substitute $1-\frac{x}{12}$ for $A_y$ in Equation (3).

$\begin{array}{c}{D}_y=4-\frac{x}{6}-4\left(1-\frac{x}{12}\right)\\ =4-\frac{x}{6}-4+\frac{x}{3}\\ =\frac{-x+2x}{6}\\ =\frac{x}{6}\end{array}$

Find the influence line ordinate of vertical reaction $\left(D_y\right)$ for portion CG$\left(12\text{m}<x\le 30\text{m}\right)$.

Substitute $0$ for $A_y$ in Equation (3).

$\begin{array}{c}{D}_y=4-\frac{x}{6}-4\left(0\right)\\ =4-\frac{x}{6}\end{array}$

Thus, the equations of the influence line ordinate for $D_y$ are,

$D_y=\frac{x}{6},0\le x<12\text{m}$ (4)

$D_y=4-\frac{x}{6},12\text{m}<x\le 30\text{m}$ (5)

Refer Figure 1.

Find the equation of influence line ordinate for the vertical reaction $\left(F_y\right)$ using force equilibrium equation.

Consider the vertical forces equilibrium condition, take the upward force as positive $\left(\uparrow +\right)$ and downward force as negative $\left(\downarrow -\right)$.

$\begin{array}{l}\Sigma F_y=0\\ A_y+D_y+F_y=1\\ F_y=1-A_y-D_y\end{array}$ (6)

Find the influence line ordinate of vertical reaction $\left(F_y\right)$ for portion AC$\left(0\le x<12\text{m}\right)$.

Substitute $1-\frac{x}{12}$ for $A_y$ and $\frac{x}{6}$ for $D_y$ in Equation (6).

$\begin{array}{c}{F}_y=1-\left(1-\frac{x}{12}\right)-\left(\frac{x}{6}\right)\\ =1-1+\frac{x}{12}-\frac{x}{6}\\ =-\frac{x}{12}\end{array}$

Find the influence line ordinate of vertical reaction $\left(F_y\right)$ for portion AC$\left(12\text{m}<x\le 30\text{m}\right)$.

Substitute $0$ for $A_y$ and $4-\frac{x}{6}$ for $D_y$ in Equation (6).

$\begin{array}{c}{F}_y=1-\left(0\right)-\left(4-\frac{x}{6}\right)\\ =1-4+\frac{x}{6}\\ =\frac{x}{6}-3\end{array}$

Thus, the equations of the influence line ordinate for $F_y$ are,

$F_y=-\frac{x}{12},0\le x<12\text{m}$ (7)

$F_y=\frac{x}{6}-3,12\text{m}<x\le 30\text{m}$ (8)

Find the equation of shear at B of portion AB$\left(0\le x<6\text{m}\right)$.

Sketch the free body diagram of the section AB as shown in Figure 2.

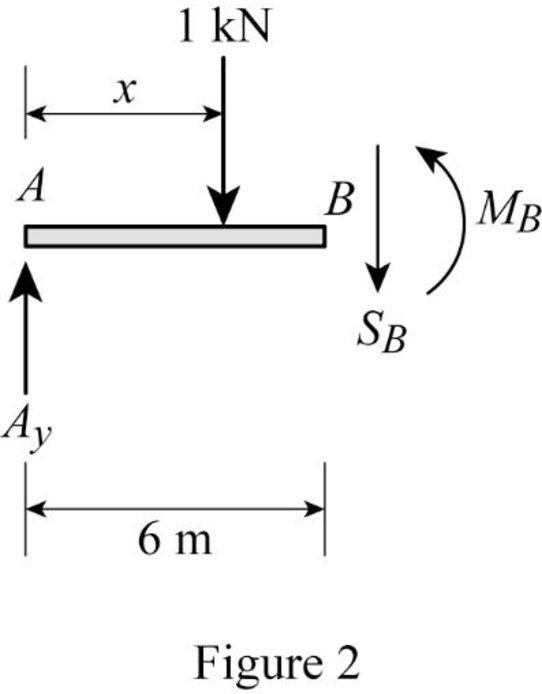
Refer Figure 2.

Apply equilibrium equation of forces.

Consider upward force as positive $\left(\uparrow +\right)$ and downward force as negative $\left(\downarrow -\right)$.

$\Sigma F_y=0$

$\begin{array}{l}{A}_y-1-S_B=0\\ S_B=A_y-1\end{array}$

Substitute $1-\frac{x}{12}$ for $A_y$.

$\begin{array}{c}{S}_B=\left(1-\frac{x}{12}\right)-1\\ =-\frac{x}{12}\end{array}$

Find the equation of shear at B of portion BG$\left(6\text{m}<x\le 30\text{m}\right)$.

Sketch the free body diagram of the section BG as shown in Figure 3.

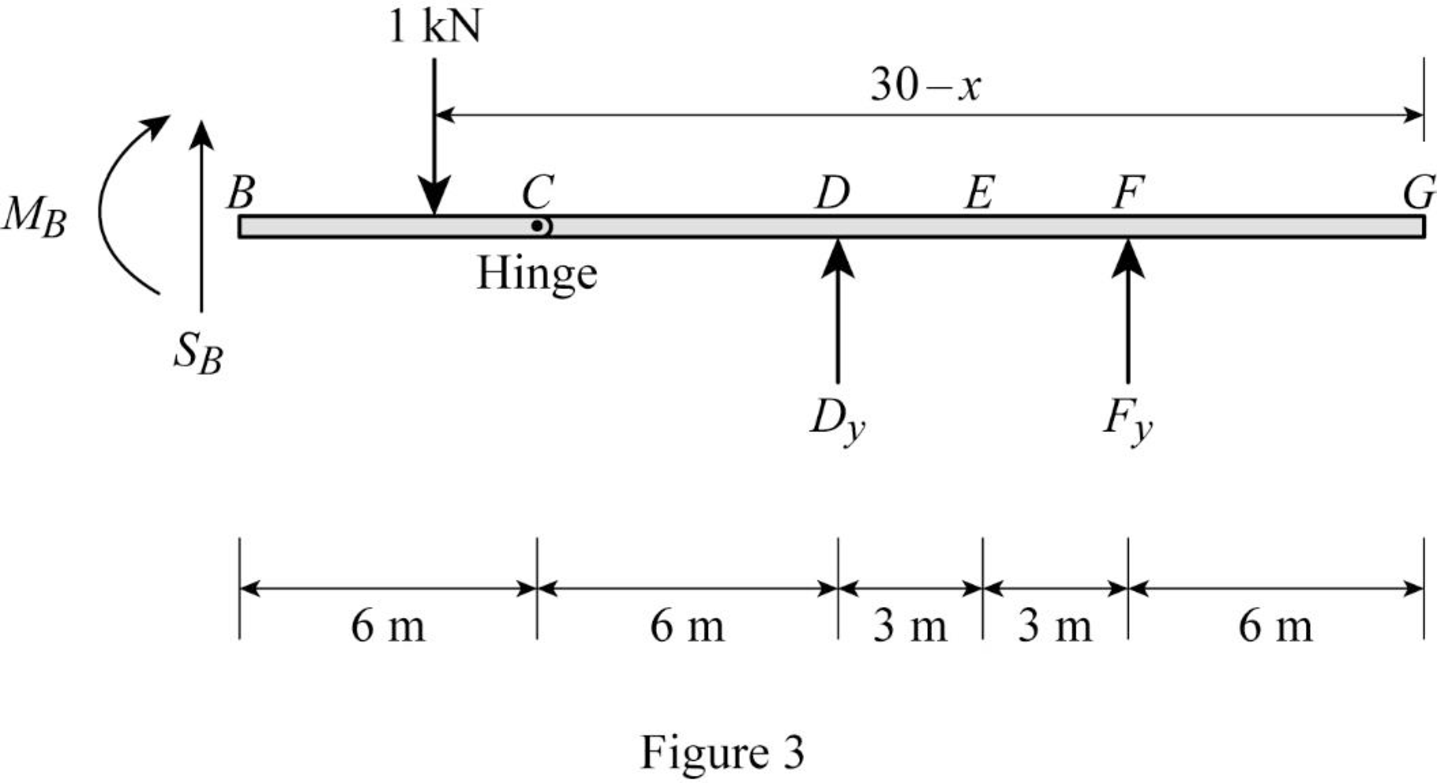
Refer Figure 3.

Apply equilibrium equation of forces.

Consider upward force as positive $\left(\uparrow +\right)$ and downward force as negative $\left(\downarrow -\right)$.

$\Sigma F_y=0$

$\begin{array}{l}{S}_B-1+D_y+F_y=0\\ S_B=1-D_y-F_y\end{array}$ (9)

Find the influence line ordinate of shear at B$\left(S_B\right)$ for portion BC $\left(6\text{m}<x<12\text{m}\right)$.

Substitute $\frac{x}{6}$ for $D_y$ and $-\frac{x}{12}$ for $F_y$ in Equation (9).

$\begin{array}{c}{S}_B=1-\left(\frac{x}{6}\right)-\left(-\frac{x}{12}\right)\\ =1-\frac{x}{6}+\frac{x}{12}\\ =1-\frac{x}{12}\end{array}$

Find the influence line ordinate of shear at B$\left(S_B\right)$ for portion CG$\left(12\text{m}<x\le 30\text{m}\right)$.

Substitute $4-\frac{x}{6}$ for $D_y$ and $\frac{x}{6}-3$ for $F_y$ in Equation (9).

$\begin{array}{c}{S}_B=1-\left(4-\frac{x}{6}\right)-\left(\frac{x}{6}-3\right)\\ =1-4+\frac{x}{6}-\frac{x}{6}+3\\ =-3+0+3\\ =0\end{array}$

Thus, the equations of the influence line ordinate for $S_B$ are,

$S_B=-\frac{x}{12},0\le x<6\text{m}$ (10)

$S_B=1-\frac{x}{12},6\text{m}<x<12\text{m}$ (11)

$S_B=0,12\text{m}<x\le 30\text{m}$ (12)

Find the influence line ordinate of $S_B$ using Equation (10), (11), and (12) and summarize the values in Table 1.

x (m)	Points	Influence line ordinate of $S_B$$\left(\text{kN/kN}\right)$
0	A	0
6	$B^{-}$	‑0.5
6	$B^{+}$	0.5
12	C	0
18	D	0
21	E	0
24	F	0
30	G	0

Sketch the influence line diagram for the shear at pointB as shown in Figure 4.

Influence line for moment at point B:

Refer Figure 2.

Find the equation of bending moment at B of portion AB$\left(0\le x<6\text{m}\right)$.

Take moment at B.

Consider clockwise moment as positive and anticlockwise moment as negative.

$M_B=A_y\left(6\right)-1\left(6-x\right)$

Substitute $1-\frac{x}{12}$ for $A_y$.

$\begin{array}{c}{M}_B=\left(1-\frac{x}{12}\right)\left(6\right)-1\left(6-x\right)\\ =6-\frac{x}{2}+6+x\\ =\frac{x}{2}\end{array}$

Refer Figure 3.

Find the equation of bending moment at B of portion BG$\left(6\text{m}<x\le 30\text{m}\right)$.

Take moment at B.

Consider clockwise moment as negative and anticlockwise moment as positive.

$\begin{array}{c}{M}_B=-1\left[24-\left(30-x\right)\right]+D_y\left(12\right)+F_y\left(18\right)\\ =-24+30-x+12D_y+18F_y\\ =6-x+12D_y+18F_y\end{array}$ (13)

Find the influence line ordinate of moment at B$\left(M_B\right)$ for portion BC$\left(6\text{m}<x<12\text{m}\right)$.

Substitute $\frac{x}{6}$ for $D_y$ and $-\frac{x}{12}$ for $F_y$ in Equation (13).

$\begin{array}{c}{M}_B=6-x+12\left(\frac{x}{6}\right)+18\left(-\frac{x}{12}\right)\\ =6-x+2x-\frac{3x}{2}\\ =6-\frac{x}{2}\end{array}$

Find the influence line ordinate of moment at B $\left(M_B\right)$ for portion CG$\left(12\text{m}<x\le 30\text{m}\right)$.

Substitute $4-\frac{x}{6}$ for $D_y$ and $\frac{x}{6}-3$ for $F_y$ in Equation (13).

$\begin{array}{c}{M}_B=-6+x-12\left(4-\frac{x}{6}\right)-18\left(\frac{x}{6}-3\right)\\ =-6+x-48+2x-3x+54\\ =0\end{array}$

Thus, the equations of the influence line ordinate for $M_B$ are,

$M_B=\frac{x}{2},0\le x<6\text{m}$ (14)

$M_B=6-\frac{x}{2},6\text{m}<x<12\text{m}$ (15)

$M_B=0,12\text{m}<x\le 30\text{m}$ (16)

Find the influence line ordinate of $M_B$ using Equation (14), (15), and (16) and summarize the values in Table 2.

x (m)	Points	Influence line ordinate of $M_B$$\left(\text{kN-m/kN}\right)$
0	A	0
6	$B$	‑3
12	C	0
18	D	0
21	E	0
24	F	0
30	G	0

Sketch the influence line diagram for the bending moment at point B as shown in Figure 5.

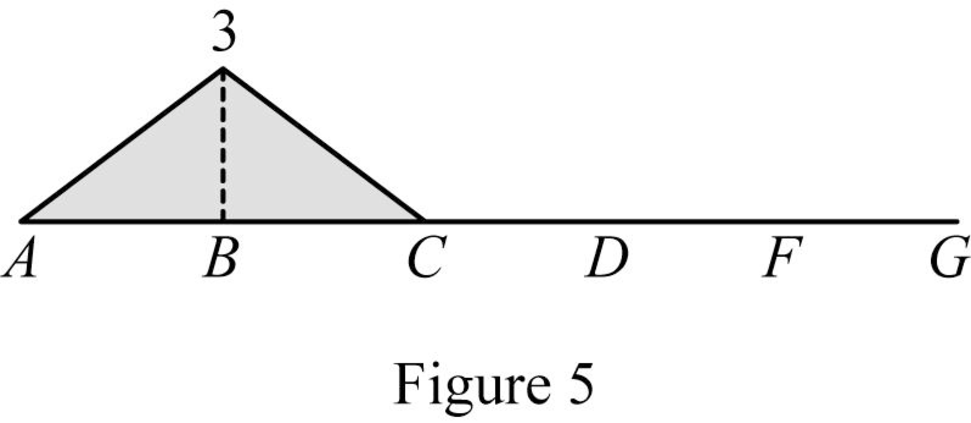
Influence line for shear at hinge C:

Apply a 1 kN unit moving load at a distance of x from left end A.

Sketch the free body diagram of frame as shown in Figure 6.

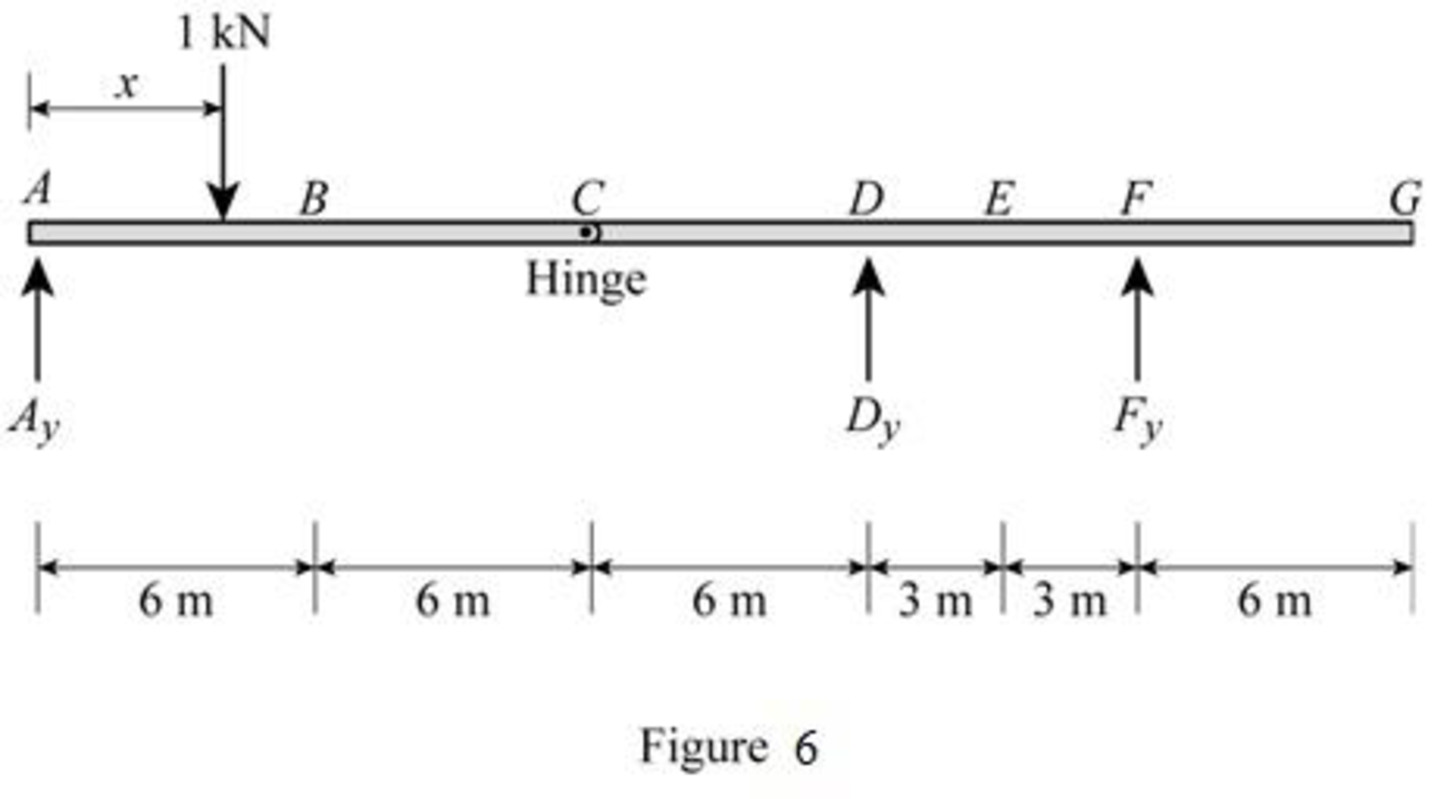
Refer Figure 6.

Consider the unit load at a variable position x to the left hinge C. (placed portion AC of the beam $0\le x<12\text{m}$).

Find the vertical support reaction $\left(A_y\right)$ at A for portion AC.

Take Moment at hinge C from left end A.

Consider clockwise moment as positive and anticlockwise moment as negative.

$\begin{array}{l}\Sigma M_C^{AC}=0\\ A_y\left(12\right)-1\left(12-x\right)=0\\ 12A_y=12-x\\ A_y=1-\frac{x}{12}\end{array}$

Consider the unit load at a variable position x to the right hinge C. (Place portion CG of the beam $12\text{m}<x\le 30\text{m}$).

Find the vertical support reaction $\left(A_y\right)$ at A for portion CG.

Take Moment at hinge C from left end A.

Consider clockwise moment as positive and anticlockwise moment as negative.

$\begin{array}{l}\Sigma M_C^{AC}=0\\ A_y\left(12\right)=0\\ A_y=0\end{array}$

Thus, the equations of the influence line ordinate for $A_y$ are,

$A_y=1-\frac{x}{12},0\le x<12\text{m}$ (17)

$A_y=0,12\text{m}<x\le 30\text{m}$ (18)

Refer Figure 1.

Find the equation of influence line ordinate for the vertical reaction $\left(D_y\right)$ using equilibrium equation.

Apply moment equilibrium at F.

Consider clockwise moment as positive and anticlockwise moment as negative.

$\begin{array}{l}\Sigma M_F=0\\ A_y\left(24\right)+D_y\left(6\right)-1\left(24-x\right)=0\\ 6D_y=24-x-24A_y\\ D_y=4-\frac{x}{6}-4A_y\end{array}$ (19)

Find the influence line ordinate of vertical reaction $\left(D_y\right)$ for portion AC$\left(0\le x<12\text{m}\right)$.

Substitute $1-\frac{x}{12}$ for $A_y$ in Equation (19).

$\begin{array}{c}{D}_y=4-\frac{x}{6}-4\left(1-\frac{x}{12}\right)\\ =4-\frac{x}{6}-4+\frac{x}{3}\\ =\frac{-x+2x}{6}\\ =\frac{x}{6}\end{array}$

Find the influence line ordinate of vertical reaction $\left(D_y\right)$ for portion CG$\left(12\text{m}<x\le 30\text{m}\right)$.

Substitute $0$ for $A_y$ in Equation (19).

$\begin{array}{c}{D}_y=4-\frac{x}{6}-4\left(0\right)\\ =4-\frac{x}{6}\end{array}$

Thus, the equations of the influence line ordinate for $D_y$ are,

$D_y=\frac{x}{6},0\le x<12\text{m}$ (20)

$D_y=4-\frac{x}{6},12\text{m}<x\le 30\text{m}$ (21)

Refer Figure 1.

Find the equation of influence line ordinate for the vertical reaction $\left(F_y\right)$ using force equilibrium equation.

Consider the vertical forces equilibrium condition, take the upward force as positive $\left(\uparrow +\right)$ and downward force as negative $\left(\downarrow -\right)$.

$\begin{array}{l}\Sigma F_y=0\\ A_y+D_y+F_y=1\\ F_y=1-A_y-D_y\end{array}$ (22)

Find the influence line ordinate of vertical reaction $\left(F_y\right)$ for portion AC$\left(0\le x<12\text{m}\right)$.

Substitute $1-\frac{x}{12}$ for $A_y$ and $\frac{x}{6}$ for $D_y$ in Equation (22).

$\begin{array}{c}{F}_y=1-\left(1-\frac{x}{12}\right)-\left(\frac{x}{6}\right)\\ =1-1+\frac{x}{12}-\frac{x}{6}\\ =-\frac{x}{12}\end{array}$

Find the influence line ordinate of vertical reaction $\left(F_y\right)$ for portion AC$\left(12\text{m}<x\le 30\text{m}\right)$.

Substitute $0$ for $A_y$ and $4-\frac{x}{6}$ for $D_y$ in Equation (22).

$\begin{array}{c}{F}_y=1-\left(0\right)-\left(4-\frac{x}{6}\right)\\ =1-4+\frac{x}{6}\\ =\frac{x}{6}-3\end{array}$

Thus, the equations of the influence line ordinate for $F_y$ are,

$F_y=-\frac{x}{12},0\le x<12\text{m}$ (23)

$F_y=\frac{x}{6}-3,12\text{m}<x\le 30\text{m}$ (24)

Find the equation of shear at C of portion AC$\left(0\le x<12\text{m}\right)$.

Sketch the free body diagram of the section AC as shown in Figure 7.

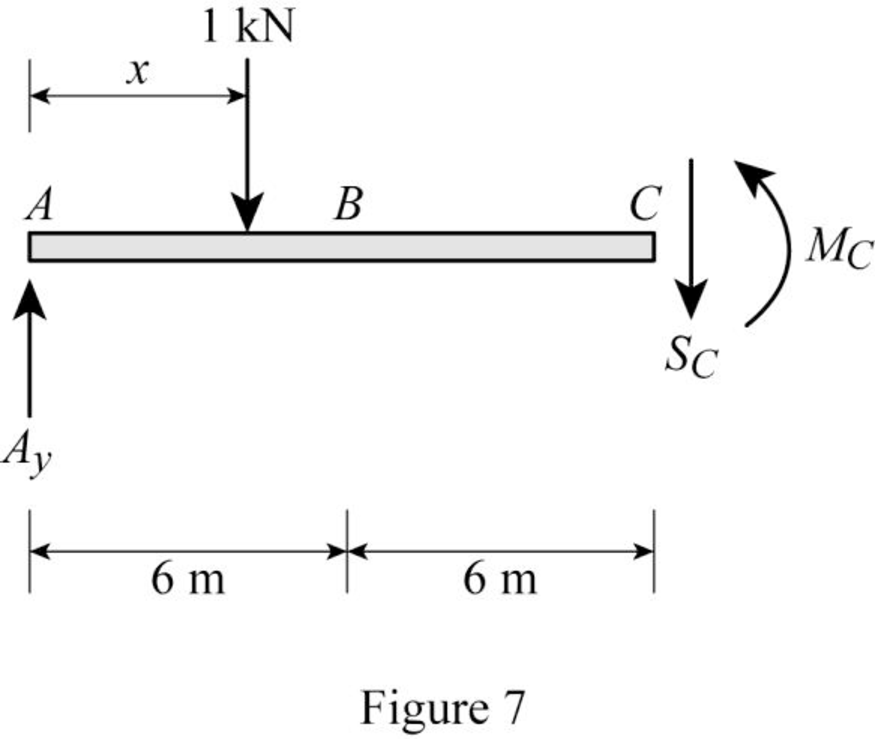
Refer Figure 7.

Apply equilibrium equation of forces.

Consider upward force as positive $\left(\uparrow +\right)$ and downward force as negative $\left(\downarrow -\right)$.

$\Sigma F_y=0$

$\begin{array}{l}{A}_y-1-S_C=0\\ S_C=A_y-1\end{array}$

Substitute $1-\frac{x}{12}$ for $A_y$.

$\begin{array}{c}{S}_C=\left(1-\frac{x}{12}\right)-1\\ =-\frac{x}{12}\end{array}$

Find the equation of shear at C of portion CG $\left(12\text{m}<x\le 30\text{m}\right)$.

Sketch the free body diagram of the section CG as shown in Figure 8.

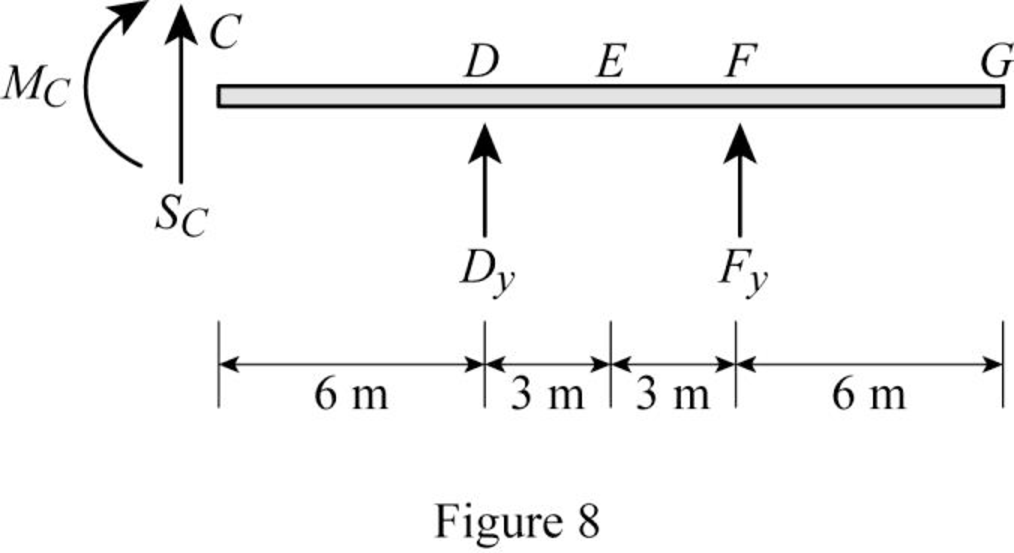
Refer Figure 8.

Apply equilibrium equation of forces.

Consider upward force as positive $\left(\uparrow +\right)$ and downward force as negative $\left(\downarrow -\right)$.

$\Sigma F_y=0$

$\begin{array}{l}{S}_C-1+D_y+F_y=0\\ S_C=1-D_y-F_y\end{array}$ (25)

Substitute $4-\frac{x}{6}$ for $D_y$ and $\frac{x}{6}-3$ for $F_y$ in Equation (25).

$\begin{array}{c}{S}_C=1-\left(4-\frac{x}{6}\right)-\left(\frac{x}{6}-3\right)\\ =1-4+\frac{x}{6}-\frac{x}{6}+3\\ =-3+0+3\\ =0\end{array}$

Thus, the equations of the influence line ordinate for $S_C$ are,

$S_C=-\frac{x}{12},0\le x<12\text{m}$ (26)

$S_C=0,12\text{m}<x\le 30\text{m}$ (27)

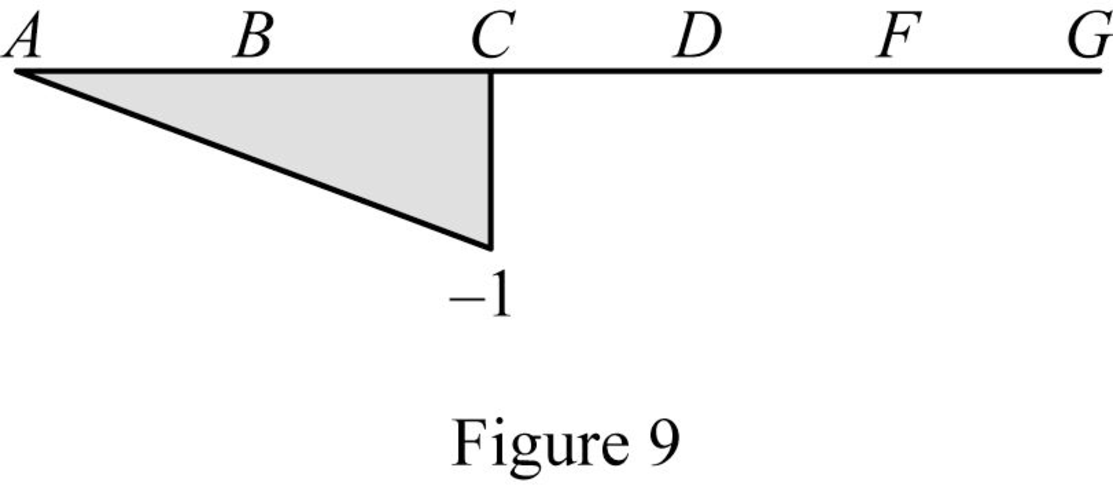
Find the influence line ordinate of $S_C$ using Equation (26) and (27) and summarize the values in Table 3.

x (m)	Points	Influence line ordinate of $S_C$$\left(\text{kN/kN}\right)$
0	A	0
6	$B$	‑0.5
12	$C^{-}$	‑1
12	$C^{+}$	0
18	D	0
21	E	0
24	F	0
30	G	0

Sketch the influence line diagram for the shear at point C as shown in Figure 9.