
Concept explainers
Draw the influence lines for the force in member CD, CI, DI, and DJ.
Explanation of Solution
Calculation:
Find the support reactions.
Apply 1 k moving load from A to G in the bottom chord member.
Draw the free body diagram of the truss as in Figure 1.
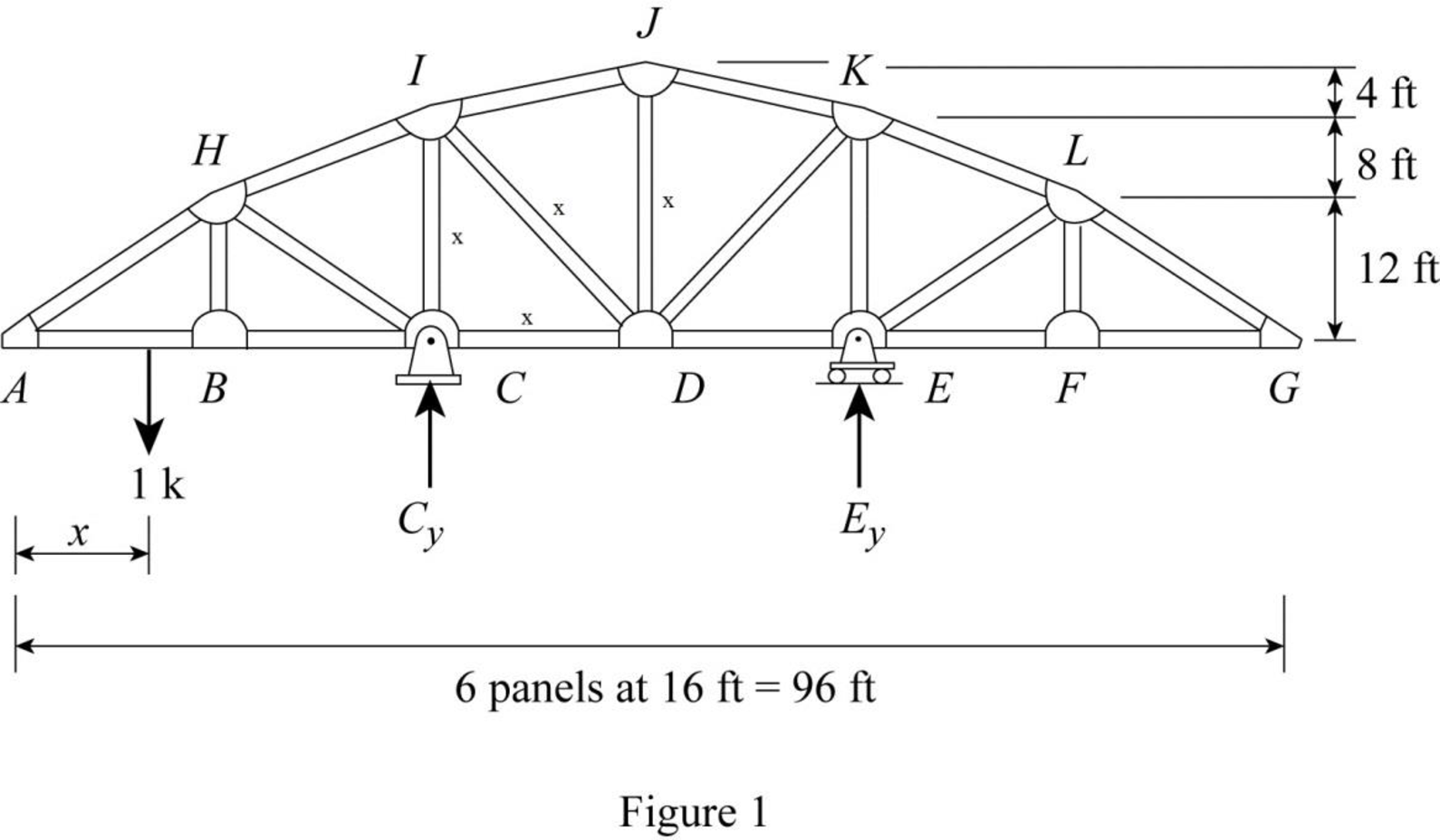
Refer Figure 1,
Find the reaction at C and E when 1 k load placed from A to G.
Apply moment equilibrium at C.
Apply force equilibrium equation along vertical.
Consider the upward force as positive
Influence line for the force in member CD.
The expressions for the member force
Draw the free body diagram of the section as shown in Figure 2.
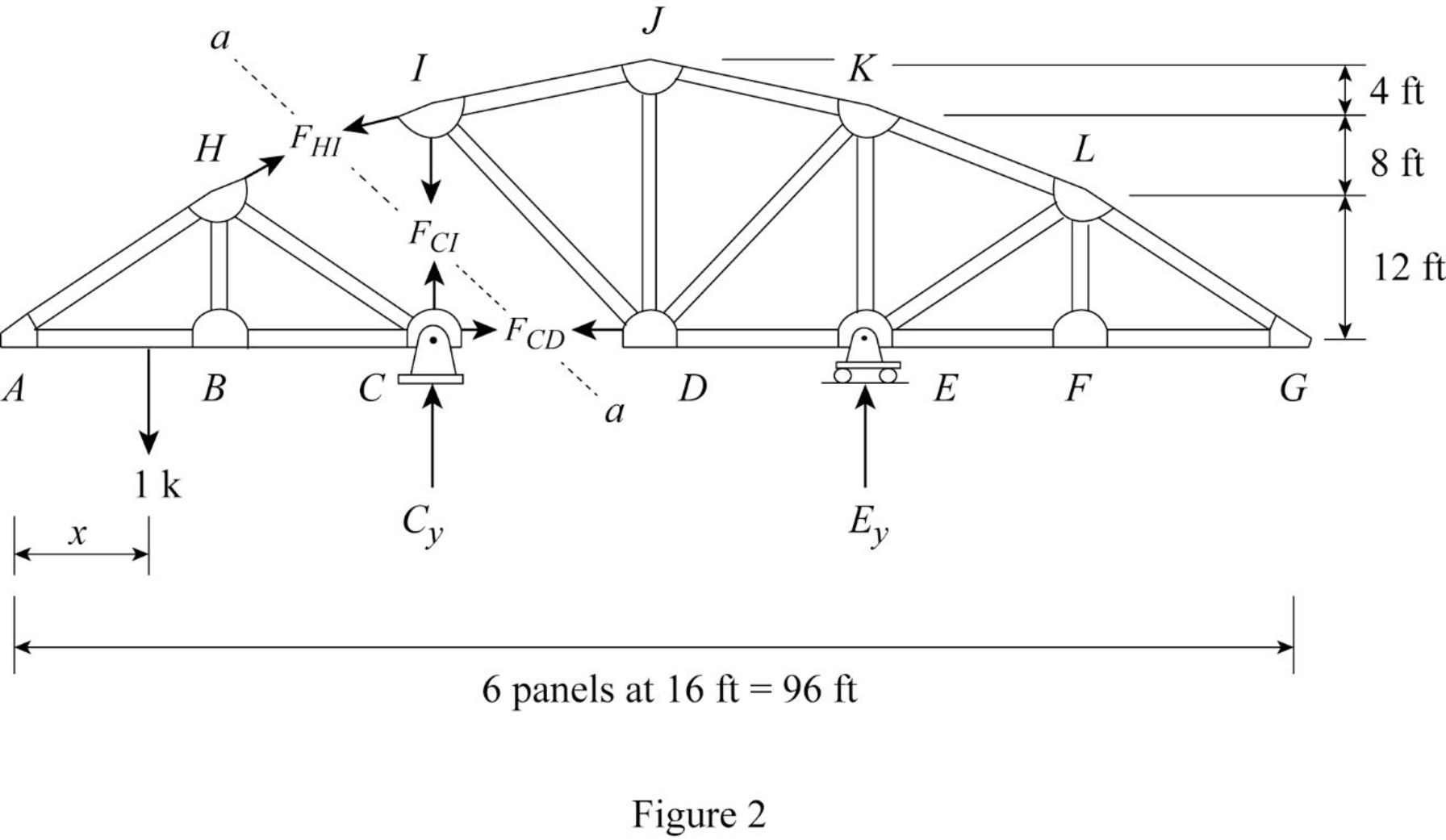
Refer Figure 2.
Apply 1 k load just the left of C
Find the equation of member force CD from A to C.
Consider the section DG.
Apply moment equilibrium equation at I.
Consider clockwise moment as negative and anticlockwise moment as positive.
Substitute
Apply 1 k load just the right of C
Find the equation of member force CD from C to G.
Consider the section AC.
Apply moment equilibrium equation at I.
Consider clockwise moment as positive and anticlockwise moment as negative.
Thus, the equation of force in the member CD,
Find the force in member CD using the Equation (1) and (2) and then summarize the value in Table 1.
| x (ft) | Apply 1 k load | Force in member CD (k) | Influence line ordinate for the force in member CD (k/k) |
| 0 | A | ||
| 16 | B | ||
| 32 | C | 0 | 0 |
| 48 | D | 0 | 0 |
| 64 | E | 0 | 0 |
| 80 | F | 0 | 0 |
| 96 | G | 0 | 0 |
Sketch the influence line diagram for ordinate for the force in member CD using Table 1 as shown in Figure 3.

Influence line for the force in member CI.
Refer Figure 2.
Apply 1 k load just the left of C
Find the equation of member force CI from A to C.
Consider the section AC.
Apply moment equilibrium equation at H.
Consider clockwise moment as negative and anticlockwise moment as positive.
Substitute
Apply 1 k load just the right of C
Find the equation of member force CI from C to G.
Consider the section AC.
Apply moment equilibrium equation at H.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member CI,
Find the force in member CI using the Equation (1) and (2) and then summarize the value in Table 2.
| x (ft | Apply 1 k load | Force in member CI (k) | Influence line ordinate for the force in member CI (k/k) |
| 0 | A | ||
| 16 | B | ||
| 32 | C | 0 | |
| 48 | D | ||
| 64 | E | 0 | |
| 80 | F | 0.5 | |
| 96 | G | 1 |
Sketch the influence line diagram for ordinate for the force in member CI using Table 2 as shown in Figure 4.
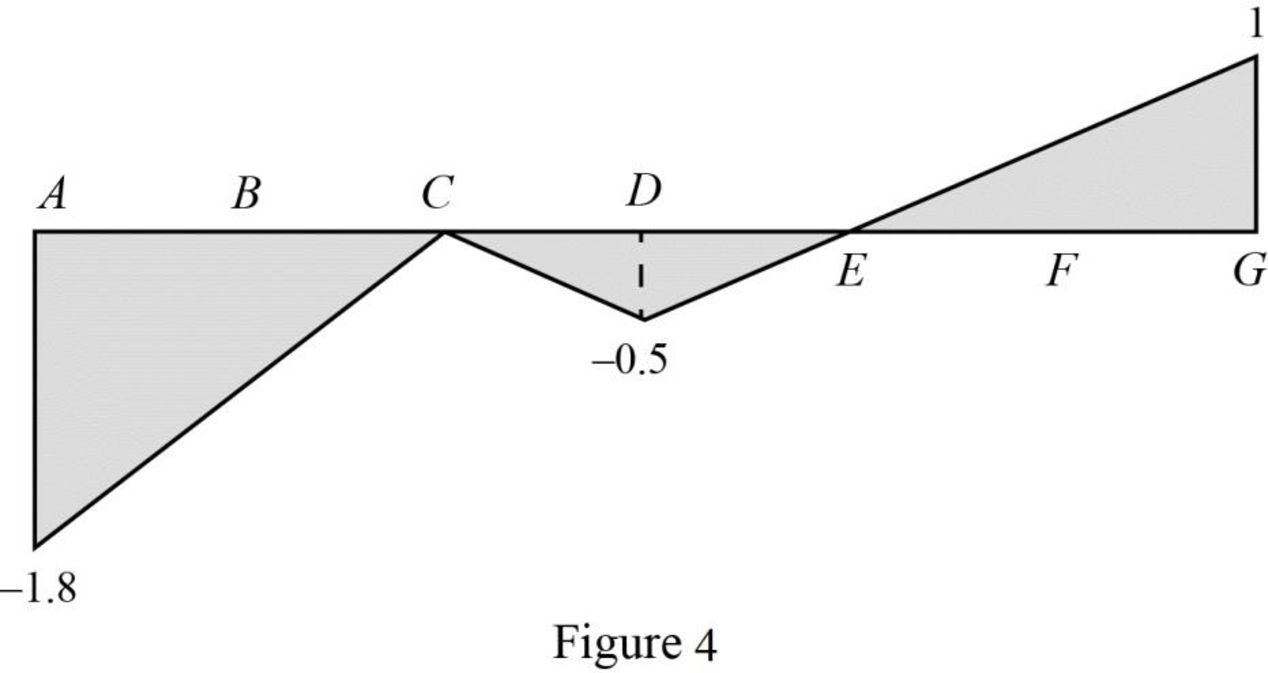
Influence line for the force in member DI.
The expressions for the member force
Draw the free body diagram of the section bb as shown in Figure 5.
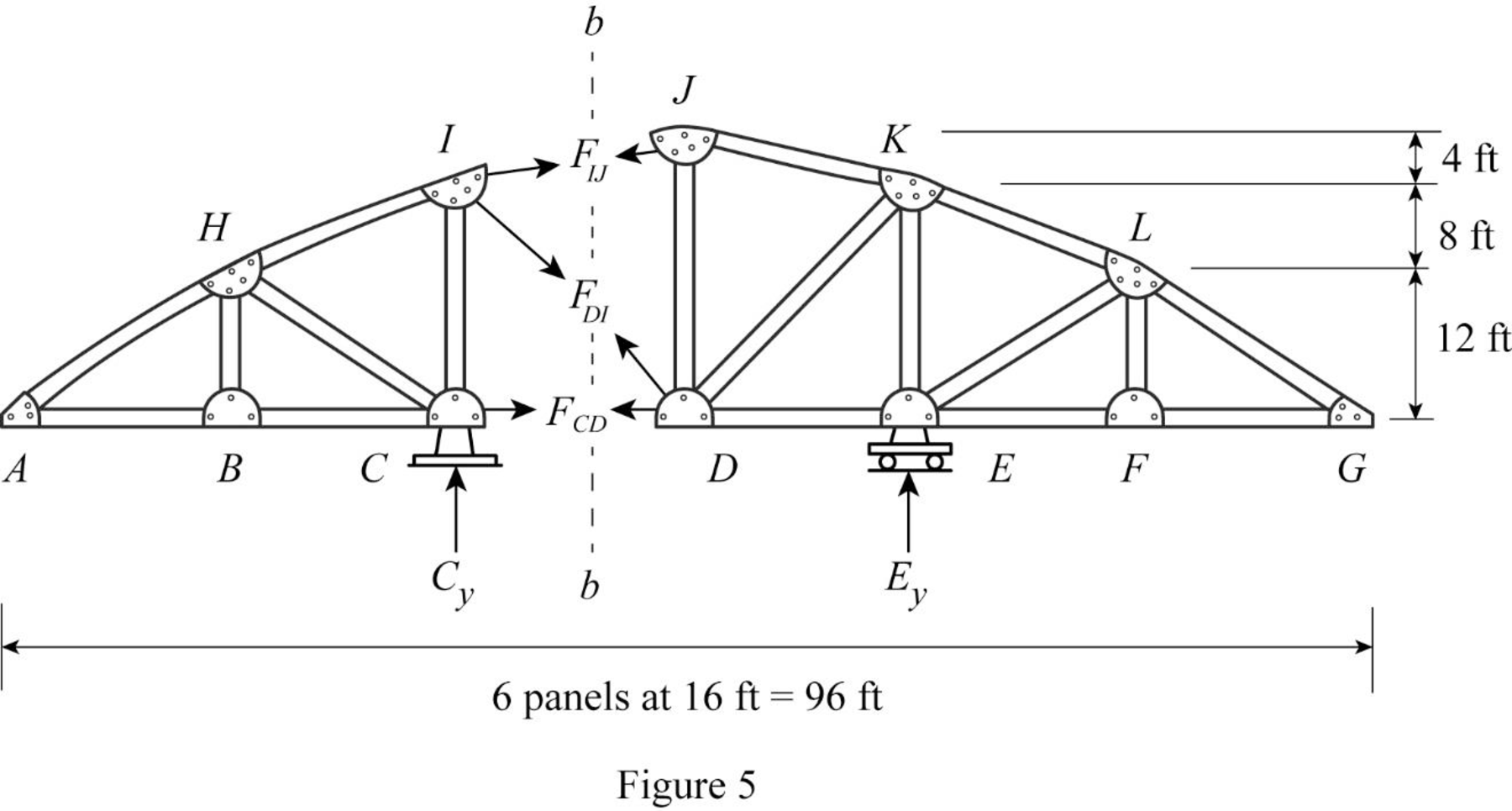
Refer Figure 5.
Apply 1 k load just the left of C
Find the equation of member force DI from A to C.
Consider the section DG.
Apply moment equilibrium equation at J.
Consider clockwise moment as negative and anticlockwise moment as positive.
Substitute
Apply 1 k load just the right of C
Find the equation of member force DI from C to G.
Consider the section AC.
Apply moment equilibrium equation at J.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member DI,
Find the force in member DI using the Equation (5) and (6) and then summarize the value in Table 3.
| x (ft) | Apply 1 k load | Force in member DI (k) | Influence line ordinate for the force in member DI (k/k) |
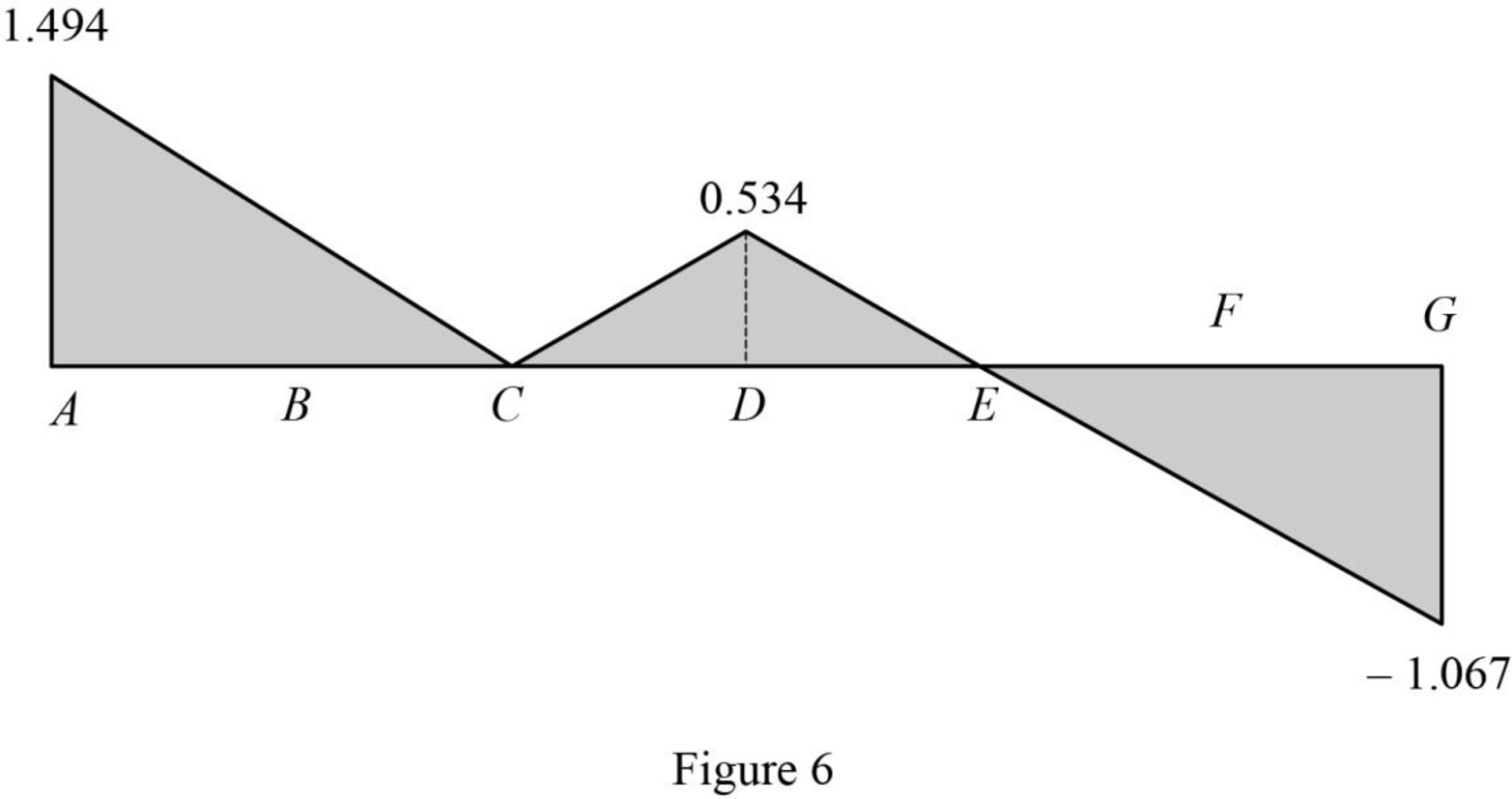
| 0 | A | 1.494 | |
| 16 | B | 0.747 | |
| 32 | C | 0 | |
| 48 | D | 0.534 | |
| 64 | E | 0 | 0 |
| 80 | F | ||
| 96 | G |
Sketch the influence line diagram for ordinate for the force in member DI using Table 3 as shown in Figure 6.
Influence line for the force in member DJ.
The expressions for the member force
Draw the free body diagram of the section cc as shown in Figure 7.
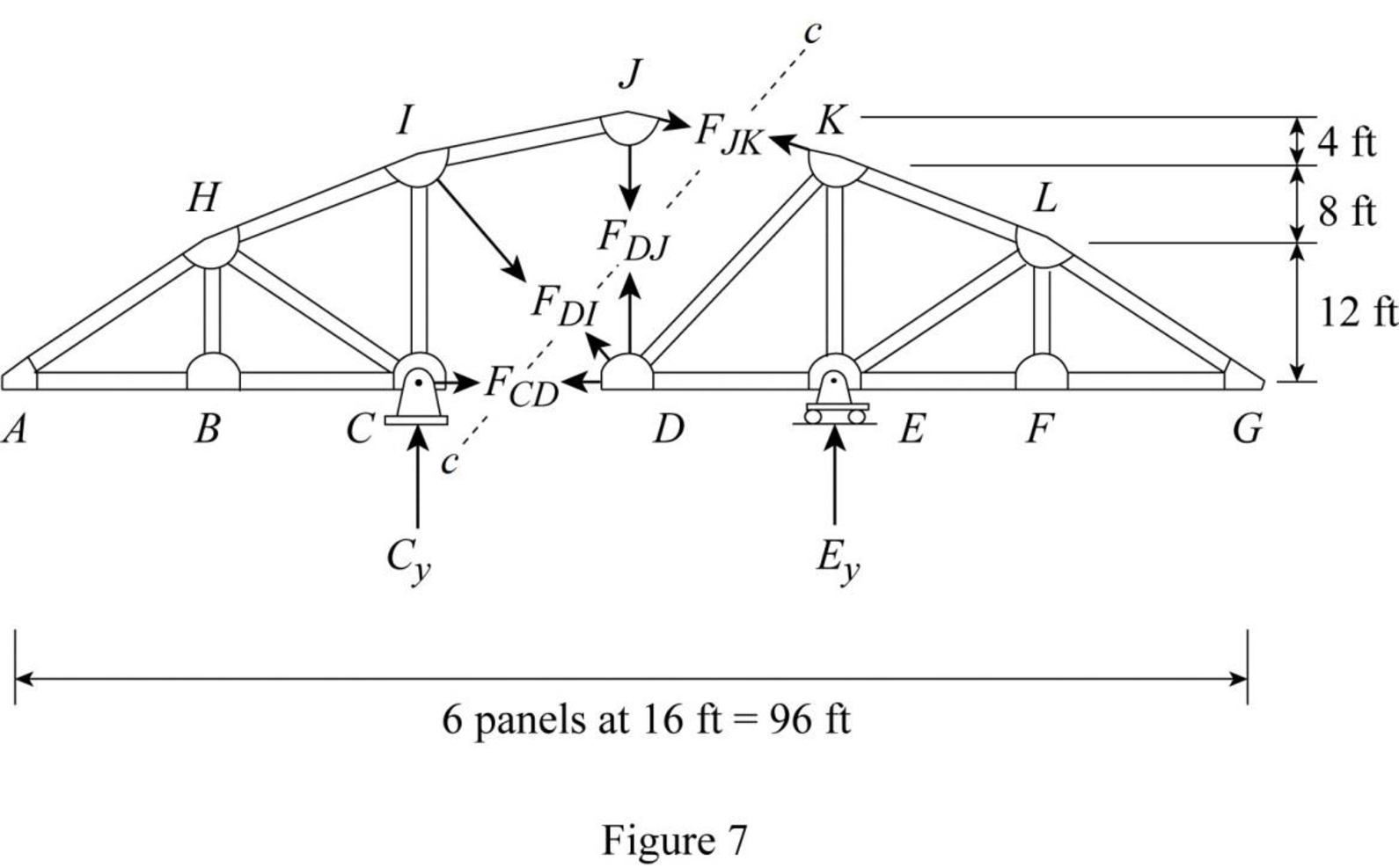
Refer Figure 7.
Apply 1 k load just the left of C
Find the equation of member force DJ from A to C.
Consider the section DG.
Apply moment equilibrium equation at C.
The member force DI is resolved in horizontal and vertical.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Apply 1 k load just the right of C
Find the equation of member force DJ from C to G.
Consider the section DG.
Apply moment equilibrium equation at K.
The member force DI is resolved in horizontal and vertical.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute 0 for
Thus, the equation of force in the member DJ,
Find the force in member DJ using the Equation (7) and (8) and then summarize the value in Table 4.
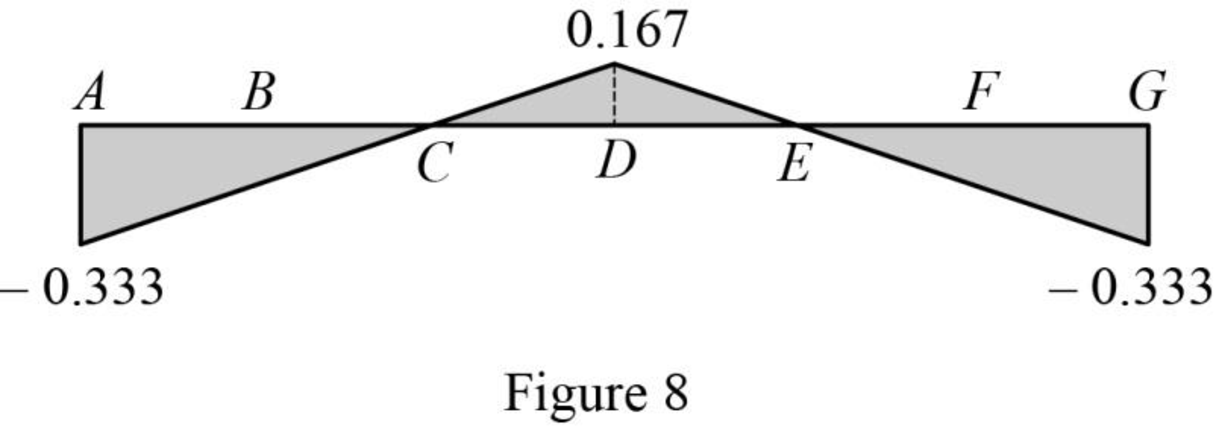
| x (ft) | Apply 1 k load | Force in member DJ (k) | Influence line ordinate for the force in member DJ (k/k) |
| 0 | A | ||
| 16 | B | ||
| 32 | C | 0 | |
| 48 | D | 0.167 | |
| 64 | E | 0 | |
| 80 | F | ||
| 96 | G |
Sketch the influence line diagram for ordinate for the force in member DJ using Table 4 as shown in Figure 8.
Want to see more full solutions like this?
Chapter 8 Solutions
Structural Analysis, SI Edition
- 6. A lake with no outlet is fed by a river with a constant flow of 1200 ft3/s. Water evaporates from the surface at a constant rate of 13 ft3/s per square mile of surface area. The surface area varies with the depth h (in feet) as A (square miles) = 4.5 + 5.5h. What is the equilibrium depth of the lake? Below what river discharge (volume flow rate) will the lake dry up?arrow_forwardProblem 5 (A, B, C and D are fixed). Find the reactions at A and D 8 k B 15 ft A -20 ft C 10 ft Darrow_forwardProblem 4 (A, B, E, D and F are all pin connected and C is fixed) Find the reactions at A, D and F 8 m B 6m E 12 kN D F 4 marrow_forward
- Problem 1 (A, C and D are pins) Find the reactions and A, C and D. D 6 m B 12 kN/m 8 m A C 6 marrow_forwardUniform Grade of Pipe Station of Point A is 9+50.00. Elevation Point A = 250.75.Station of Point B is 13+75.00. Elevation Point B = 244.10 1) Calculate flowline of pipe elevations at every 50 ft. interval (Half Station). 2) Tabulate station and elevation for each station like shown on example 3) Draw Sketcharrow_forward40m 150N B 40marrow_forward
- Note: Please accurately answer it!. I'll give it a thumbs up or down based on the answer quality and precision. Question: What is the group name of Sample B in problem 3 from the image?. By also using the ASTM flow chart!. This unit is soil mechanics btwarrow_forwardPick the rural location of a project site in Victoria, and its catchment area-not bigger than 25 sqkm, and given the below information, determine the rainfall intensity for ARI = 5, 50, 100 year storm event. Show all the details of the procedure. Each student must propose different length of streams and elevations. Use fig below as a sample only. Pt. E-ht. 95.0 200m 600m PLD-M. 91.0 300m Pt. C-93.0 300m PL.B-ht. 92.0 PL.F-ht. 96.0 500m Pt. A-M. 91.00 To be deemed satisfactory the solution must include: Q.F1.1.Choice of catchment location Q.F1.2. A sketch displaying length of stream and elevation Q.F1.3. Catchment's IFD obtained from the Buro of Metheorology for specified ARI Q.F1.4.Calculation of the time of concentration-this must include a detailed determination of the equivalent slope. Q.F1.5.Use must be made of the Bransby-Williams method for the determination of the equivalent slope. Q.F1.6.The graphical display of the estimation of intensities for ARI 5,50, 100 must be shown.arrow_forwardQUANTITY SURVEYINGarrow_forward
