Chapter 8, Problem 44CP

Starting from rest, a 64.0-kg person bungee jumps from a tethered hot-air balloon 65.0 m above the ground. The bungee cord has negligible mass and unstretched length 25.8 m. One end is tied to the basket of the balloon and the other end to a harness around the person’s body. The cord is modeled as a spring that obeys Hooke’s law with a spring constant of 81.0 N/m, and the person’s body is modeled as a particle. The hot-air balloon does not move. (a) Express the gravitational potential energy of the person–Earth system as a function of the person’s variable height y above the ground. (b) Express the elastic potential energy of the cord as a function of y. (c) Express the total potential energy of the person–cord–Earth system as a function of y. (d) Plot a graph of the gravitational, elastic, and total potential energies as functions of y. (e) Assume air resistance is negligible. Determine the minimum height of the person above the ground during his plunge. (f) Docs the potential energy graph show any equilibrium position or positions? If so, at what elevations? Are they stable or unstable? (g) Determine the jumper’s maximum speed.

To determine

To show: The gravitational potential energy of the person–Earth system as a function of the person’s variable height $y$ above the ground.

Answer to Problem 44CP

 The gravitational potential energy of the person–Earth system as a function of the person’s variable height $y$ above the ground is $627.2y$.

Explanation of Solution

Given info: The mass of the person is $64.0\text{kg}$, height of the hot air balloon above the ground is $65.0\text{m}$, the length of bungee cord is $25.8\text{m}$, and spring constant of bungee cord is $81.0\text{N}/\text{m}$.

The acceleration due to gravity is $9.8\text{m}/{\text{s}}^2$.

The expression for gravitational potential energy is as follows:

$U=mgy$

Here,

$m$ is the mass.

$g$ is the acceleration due to gravity.

$y$ is the height.

Substitute $64.0\text{kg}$ for $m$ and $9.8\text{m}/{\text{s}}^2$ for $g$ in the above expression.

$\begin{array}{c}U=64.0\times 9.8\times y\\ =627.2\times y\end{array}$

Conclusion:

Therefore, the gravitational potential energy of the person–Earth system as a function of the person’s variable height $y$ above the ground is $627.2y$.

To determine

To show: Elastic potential energy of cord as a function of $y$.

Answer to Problem 44CP

 The elastic potential energy of cord as a function of $y$ is $y^2-3.17\times {10}^{3}y+6.22\times {10}^4$.

Explanation of Solution

Given info: The mass of the person is $64.0\text{kg}$, height of the hot air balloon above the ground is $65.0\text{m}$, the length of bungee cord is $25.8\text{m}$, and spring constant of bungee cord is $81.0\text{N}/\text{m}$.

The expression for elastic potential energy of spring is as follows:

$U_{\text{s}}=\frac{1}{2}k{x}^2$ (1)

$k$ is spring constant.

$x$ is the extension in spring.

The cord will stretch by length x only when the person falls more than the length of the cord. Now, the height of the balloon h should be more than the length of the cord l plus the person’s height y, for safe landing.

The expression for extension in spring is as follows:

$x=h-l-y$

Here,

$h$ is height of the balloon.

$l$ is the length of cord.

$y$ is person’s height

Substitute $65.0\text{m}$ for $h$ and $25.8\text{m}$ for $l$ in the above expression.

$\begin{array}{c}x=65.0-25.8-y\\ =39.2-y\end{array}$

Substitute $39.2\text{m}-y$ for $x$ and $81.0\text{N}/\text{m}$ for $k$ in Equation (1).

$U_{\text{s}}=\frac{1}{2}\left(81.0\right){\left(39.2-y\right)}^2$

Conclusion:

Therefore, the elastic potential energy of the cord as function of $y$ is $\frac{1}{2}\left(81.0\right){\left(39.2-y\right)}^2.$

To determine

To show: The total potential energy of the person-cord–Earth system as a function of $y$.

Answer to Problem 44CP

 The total potential energy of the person-cord–Earth system as a function of $y$ is $627.2\times y+y^2\frac{1}{2}\left(81.0\right){\left(39.2-y\right)}^2$.

Explanation of Solution

Given info: The mass of the person is $64.0\text{kg}$, height of the hot air balloon above the ground is $65.0\text{m}$, the length of bungee cord is $25.8\text{m}$, and spring constant of bungee cord is $81.0\text{N}/\text{m}$.

The expression for total potential energy of the person-cord–Earth system is as follows:

$U_{\text{T}}=U+U_{\text{s}}$

Substitute $627.2\text{N}\times y$ for $U$ and $y^2-3.17\times {10}^{3}y+6.22\times {10}^4$ for $U_{\text{s}}$ in the above expression.

$U_{\text{T}}=627.2\times y+y^2\frac{1}{2}\left(81.0\right){\left(39.2-y\right)}^2$

Conclusion:

Therefore, the total potential energy of the person-cord–Earth system as a function of $y$ is $627.2\times y+y^2\frac{1}{2}\left(81.0\right){\left(39.2-y\right)}^2$.

To determine

To draw: The graph of gravitational, elastic, and total potential energies as a function of $y.$

Answer to Problem 44CP

 The graph of gravitational, elastic, and total potential energies as a function of $y$ is given below.

Explanation of Solution

Introduction:

The gravitational potential energy above the surface of the earth is directly proportional to the height of the object.

The elastic potential energy is proportional to the square of displacement.

The total potential energy is the sum of all the potential energies in the system.

Given info: The mass of the person is $64.0\text{kg}$, height of the hot air balloon above the ground is $65.0\text{m}$, the length of bungee cord is $25.8\text{m}$, and spring constant of bungee cord is $81.0\text{N}/\text{m}$.

From part (a), the expression for gravitational potential energy of person as a function of $y$ is given below:

$U=627.2\times y$.

Table for the above expression is shown below:

$y\left(\text{m}\right)$	$U\left(\text{kJ}\right)$
$0$	$0$
$10$	$6.27$
$20$	$12.54$
$30$	$18.81$
$40$	$25.08$
$50$	$31.36$
$60$	$37.6$

The graph of gravitational potential energy with displacement is shown below:

Figure(1)

From part (a), the expression for the elastic potential energy of cord as a function of $y$ is as follows:

$U_{\text{s}}=\frac{1}{2}\left(81.0\right){\left(39.2-y\right)}^2$.

The value of elastic potential energy of the cord remains zero till the person does not fall

equal to the length of cord; therefore, the value of the above equation is zero for $y$, which is greater than $39.2\text{m}$.

Table for the above expression is shown below:

$y\left(\text{m}\right)$	$U_{\text{s}}\left(\text{kJ}\right)$
$0$	$62.23$
$10$	$34.53$
$20$	$14.93$
$30$	$3.43$
$40$	$0$
$50$	$0$
$60$	$0$

The graph of elastic potential energy with displacement is represented below:

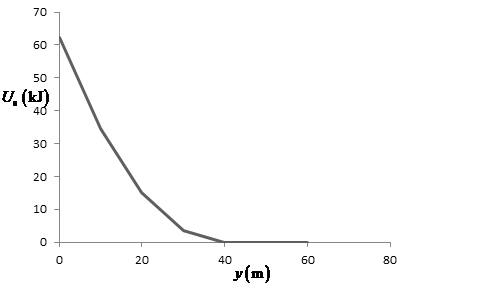
Figure(2)

From part (a), the expression for total potential energy of the person-cord–Earth system as a function of $y$ is as follows:

$U_{\text{T}}=627.2\times y+\frac{1}{2}\left(81.0\right){\left(39.2-y\right)}^2$.

When the value of $y$ is greater than $39.2\text{m}$, the value of elastic potential energy in the above expression is zero.

Table for the above expression is shown below:

$y\left(\text{m}\right)$	$U_{\text{T}}\left(\text{kJ}\right)$
$0$	$62.23$
$10$	$40.8$
$20$	$27.47$
$30$	$22.24$
$40$	$25.08$
$50$	$31.36$
$60$	$37.6$

The graph of total potential energy with displacement is represented below:

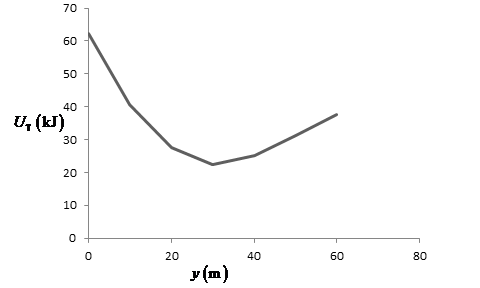
Figure(3)

To determine

 The minimum height of the person above the ground during his plunge.

Answer to Problem 44CP

 The minimum height of the person above the ground during his plunge is $19.8\text{m}$.

Explanation of Solution

Given info: The mass of the person is $64.0\text{kg}$, height of the hot air balloon above the ground is $65.0\text{m}$, the length of bungee cord is $25.8\text{m}$, and spring constant of bungee cord is $81.0\text{N}/\text{m}$.

The expression for change in total energy is as follows:

$\Delta U+\Delta U_{\text{s}}+\Delta U_{\text{k}}=0$

Here,

$\Delta U$ is the change in gravitational potential energy.

$\Delta U_{\text{s}}$ is the change in elastic potential energy.

$\Delta U_{\text{k}}$ is the change in kinetic energy.

The value of initial kinetic energy is zero, as the person is at rest.

The length of cord is $25.8\text{m}$; therefore, the length of cord is subtracted from the height of the balloon.

Substitute $-mg\left(65-y\right)$ for $\Delta U$ and $\frac{1}{2}k{\left(39.2-y\right)}^2$ for $\Delta U_{\text{s}}$ in the above expression.

$-mg\left(65-y\right)+\frac{1}{2}k{\left(39.2-y\right)}^2+\Delta U_{\text{k}}=0$

At minimum height above the ground during plunge, the person comes to rest and the change in kinetic energy is zero, as both values of initial and final kinetic energies are zero.

Substitute $0$ for $\Delta U_{\text{k}}$ in the above expression.

$\begin{array}{c}-mg\left(65-y\right)+\frac{1}{2}k{\left(39.2-y\right)}^2+0=0\\ \frac{1}{2}k{y}^2+\left(mg-k39.2\right)y+\frac{1}{2}k{\left(39.2\right)}^2-65mg=0\end{array}$

The expression for the roots of the above quadratic equation is as follows:

$h=\frac{k39.2-mg\pm \sqrt{{\left(mg-k39.2\right)}^2-4\left(\frac{1}{2}k\right)\left(\frac{1}{2}k{\left(39.2\right)}^2-65mg\right)}}{k}$

Substitute $64.0\text{kg}$ for $m$, $9.8\text{m}/{\text{s}}^2$ for $g$, and $81.0\text{N}/\text{m}$ for $k$  in the above expression.     $\begin{array}{c}h=\frac{\left(81.0\text{N}/\text{m}\right)39.2-\left(64.0\text{kg}\right)\left(9.8\text{m}/{\text{s}}^2\right)\pm \sqrt{\begin{array}{l}{\left(\left(81.0\text{N}/\text{m}\right)39.2-\left(64.0\text{kg}\right)\left(9.8\text{m}/{\text{s}}^2\right)\right)}^2\\ -4\left(\frac{1}{2}\times 81.0\text{N}/\text{m}\right)\\ \left(\begin{array}{l}\frac{1}{2}\left(81.0\text{N}/\text{m}\right){\left(39.2\right)}^2\\ -65\left(64.0\text{kg}\right)\left(9.8\text{m}/{\text{s}}^2\right)\end{array}\right)\end{array}}}{\left(81.0\text{N}/\text{m}\right)}\\ =19.8\text{m}\end{array}$

Conclusion:

Therefore, the minimum height of the person above the ground during his plunge is $19.8\text{m}$.

To determine

 Whether potential energy graph shows any equilibrium position and if so the elevation of equilibrium position, whether the equilibrium points are stable or unstable.

Answer to Problem 44CP

 The potential energy graph shows that in an equilibrium position at an elevation of $31.46\text{m}$, the equilibrium position is unstable.

Explanation of Solution

Given info: The mass of the person is $64.0\text{kg}$, height of the hot air balloon above the ground is $65.0\text{m}$, the length of bungee cord is $25.8\text{m}$, and the spring constant of bungee cord is $81.0\text{N}/\text{m}$.

The graph of potential energy shows the equilibrium position at the place where the value of total potential energy is minimum.

The expression for total potential energy is as follows:

$U_{\text{T}}=627.2\times y+\frac{1}{2}\left(81.0\right){\left(39.2-y\right)}^2$

Derive the above equation with the height of the person.

$\frac{d{U}_{\text{T}}}{dy}=627.2-\left(81.0\right)\left(39.2-y\right)$

For the expression of minima, equate the above expression equal to zero.

$\begin{array}{c}\frac{d{U}_{\text{T}}}{dy}=627.2-\left(81.0\right)\left(39.2-y\right)=0\\ y=31.46\text{m}\end{array}$

The elevation at the point of equilibrium is $31.46\text{m}$.

The person could not stop at the elevation of equilibrium position as he has kinetic energy that does not allow the person to stay at the elevation of equilibrium position. The equilibrium position is unstable.

Conclusion:

Therefore, the potential energy graph shows that in an equilibrium position at an elevation of $31.46\text{m}$, the equilibrium position is unstable.

To determine

 The jumper’s maximum speed.

Answer to Problem 44CP

 The jumper’s maximum speed is $24.12\text{m}/\text{s}$.

Explanation of Solution

Given info: The mass of the person is $64.0\text{kg}$, height of the hot air balloon above the ground is $65.0\text{m}$, the length of bungee cord is $25.8\text{m}$, and the spring constant of bungee cord is $81.0\text{N}/\text{m}$.

The expression for change in total energy is as follows:

$\Delta U+\Delta U_{\text{s}}+\Delta U_{\text{k}}=0$

Substitute $-mg\left(65-y\right)$ for $\Delta U$  and $\frac{1}{2}k{\left(39.2-y\right)}^2$ for $\Delta U_{\text{s}}$ in the above expression.

$\begin{array}{c}-mg\left(65-y\right)+\frac{1}{2}k{\left(39.2-y\right)}^2+\Delta U_{\text{k}}=0\\ \Delta U_{\text{k}}=mg\left(65-y\right)-\frac{1}{2}k{\left(39.2-y\right)}^2\end{array}$ (2)

The initial kinetic energy of the jumper is zero; hence, the change in the kinetic energy equals the kinetic energy at that position. Velocity is directly proportional to the square root of the kinetic energy; therefore, for maximum value of kinetic energy, the velocity is maximum.

Differentiate the above expression with respect to $y$.

$\frac{d\Delta U_{\text{k}}}{dy}=-mg+k\left(39.2-y\right)$

Equate $\frac{d\Delta U_{\text{k}}}{dy}$ equal to $0$ .

$\frac{d\Delta U_{\text{k}}}{dy}=0$

Substitute $-mg+k\left(39.2-y\right)$ for $\frac{d\Delta U_{\text{k}}}{dy}$ in the above expression.

$\begin{array}{c}-mg+k\left(39.2-y\right)=0\\ y=39.2-\frac{mg}{k}\end{array}$

Substitute $64.0\text{kg}$ for $m$, $9.8\text{m}/{\text{s}}^2$ for $g$, and $81.0\text{N}/\text{m}$ for $k$ in the above expression.

$\begin{array}{c}y=39.2\text{m}-\frac{\left(64.0\text{kg}\right)\left(9.8\text{m}/{\text{s}}^2\right)}{\left(81.0\text{N}/\text{m}\right)}\\ =31.46\text{m}\end{array}$

The height at which the velocity is maximum is $31.46\text{m}$.

Substitute $64.0\text{kg}$ for $m$, $9.8\text{m}/{\text{s}}^2$ for $g$, $81.0\text{N}/\text{m}$ for $k$, and $31.46\text{m}$ for $y$ in Equation (2).

$\begin{array}{c}\Delta U_{\text{k}}=\left(64.0\text{kg}\right)\left(9.8\text{m}/{\text{s}}^2\right)\left(65\text{m}-31.46\text{m}\right)-\frac{1}{2}\left(81.0\text{N}/\text{m}\right){\left(39.2-31.46\text{m}\right)}^2\\ =18610\text{J}\end{array}$

Substitute $\frac{1}{2}m{v}^2$ for $\Delta U_{\text{k}}$ in the above expression.

$\begin{array}{c}\frac{1}{2}m{v}^2=18610\text{J}\\ \text{v=}\sqrt{\frac{\text{2}\times \text{18610}}{m}}\end{array}$

Substitute $64.0\text{kg}$ for $m$ in the above expression.

$\begin{array}{c}\text{v=}\sqrt{\frac{\text{2}\times \text{18610}\text{J}}{64.0\text{kg}}}\\ =24.12\text{m}/\text{s}\end{array}$

Conclusion:

Therefore, the jumper’s maximum speed is $24.12\text{m}/\text{s}$.