
Concept explainers
Draw the influence lines for the shear and bending moment at point B.
Draw the influence lines for the shear at internal hinge C.
Explanation of Solution
Calculation:
Influence line for shear at point B:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of frame as shown in Figure 1.
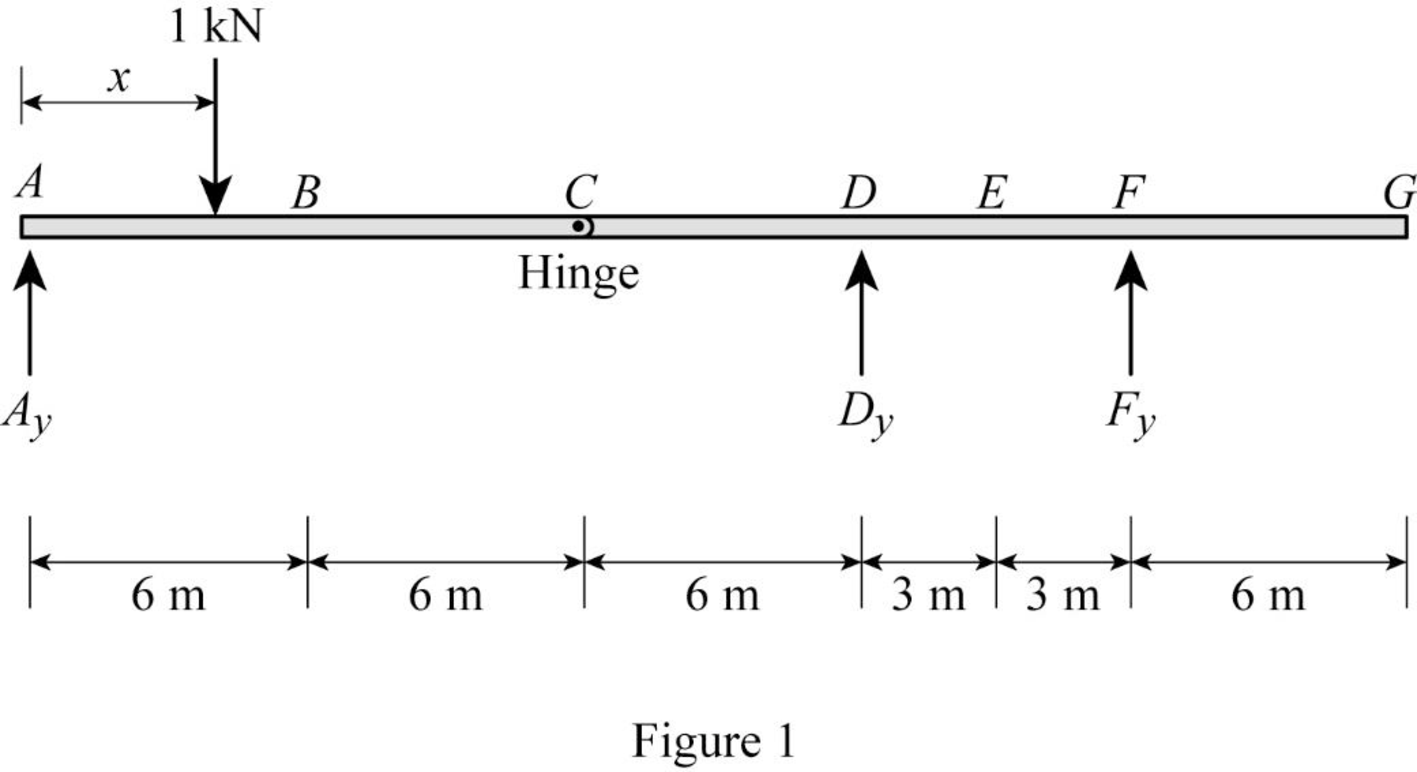
Refer Figure 1.
Consider the unit load at a variable position x to the left hinge C. (placed portion AC of the beam 0≤x<12 m).
Find the vertical support reaction (Ay) at A for portion AC.
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
ΣMACC=0Ay(12)−1(12−x)=012Ay=12−xAy=1−x12
Consider the unit load at a variable position x to the right hinge C. (Place portion CG of the beam 12 m<x≤30 m).
Find the vertical support reaction (Ay) at A for portion CG.
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
ΣMACC=0Ay(12)=0Ay=0
Thus, the equations of the influence line ordinate for Ay are,
Ay=1−x12,0≤x<12 m (1)
Ay=0,12 m<x≤30 m (2)
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction (Dy) using equilibrium equation.
Apply moment equilibrium at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
ΣMF=0Ay(24)+Dy(6)−1(24−x)=06Dy=24−x−24AyDy=4−x6−4Ay (3)
Find the influence line ordinate of vertical reaction (Dy) for portion AC (0≤x<12 m).
Substitute 1−x12 for Ay in Equation (3).
Dy=4−x6−4(1−x12)=4−x6−4+x3=−x+2x6=x6
Find the influence line ordinate of vertical reaction (Dy) for portion CG(12 m<x≤30 m).
Substitute 0 for Ay in Equation (3).
Dy=4−x6−4(0)=4−x6
Thus, the equations of the influence line ordinate for Dy are,
Dy=x6,0≤x<12 m (4)
Dy=4−x6,12 m<x≤30 m (5)
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction (Fy) using force equilibrium equation.
Consider the vertical forces equilibrium condition, take the upward force as positive (↑+) and downward force as negative (↓−).
ΣFy=0Ay+Dy+Fy=1Fy=1−Ay−Dy (6)
Find the influence line ordinate of vertical reaction (Fy) for portion AC(0≤x<12 m).
Substitute 1−x12 for Ay and x6 for Dy in Equation (6).
Fy=1−(1−x12)−(x6)=1−1+x12−x6=−x12
Find the influence line ordinate of vertical reaction (Fy) for portion AC(12 m<x≤30 m).
Substitute 0 for Ay and 4−x6 for Dy in Equation (6).
Fy=1−(0)−(4−x6)=1−4+x6=x6−3
Thus, the equations of the influence line ordinate for Fy are,
Fy=−x12,0≤x<12 m (7)
Fy=x6−3,12 m<x≤30 m (8)
Find the equation of shear at B of portion AB(0≤x<6 m).
Sketch the free body diagram of the section AB as shown in Figure 2.
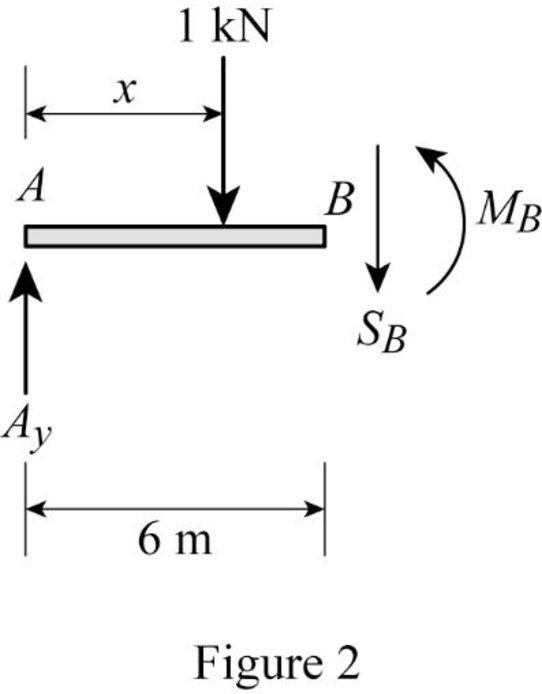
Refer Figure 2.
Apply equilibrium equation of forces.
Consider upward force as positive (↑+) and downward force as negative (↓−).
ΣFy=0
Ay−1−SB=0SB=Ay−1
Substitute 1−x12 for Ay.
SB=(1−x12)−1=−x12
Find the equation of shear at B of portion BG(6 m<x≤30 m).
Sketch the free body diagram of the section BG as shown in Figure 3.
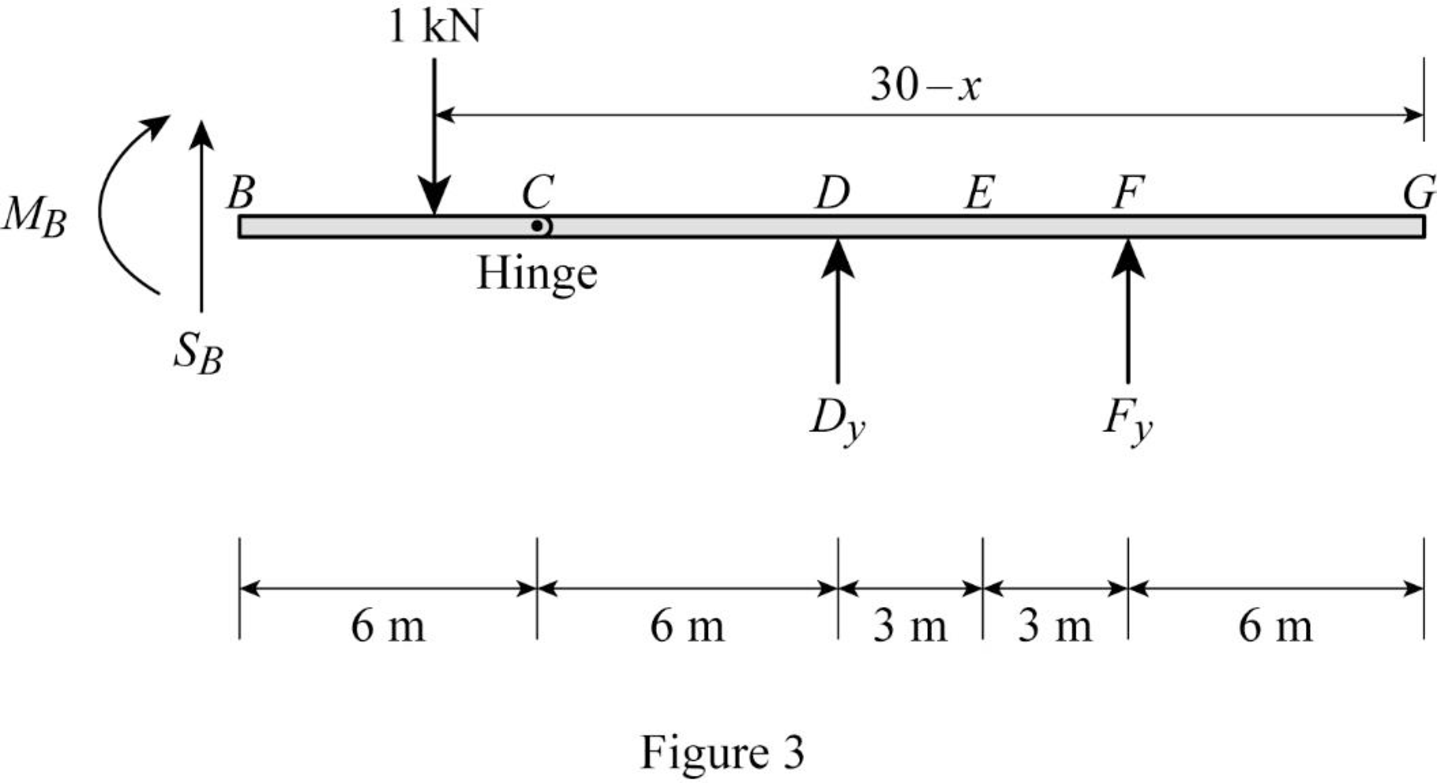
Refer Figure 3.
Apply equilibrium equation of forces.
Consider upward force as positive (↑+) and downward force as negative (↓−).
ΣFy=0
SB−1+Dy+Fy=0SB=1−Dy−Fy (9)
Find the influence line ordinate of shear at B(SB) for portion BC (6 m<x<12 m).
Substitute x6 for Dy and −x12 for Fy in Equation (9).
SB=1−(x6)−(−x12)=1−x6+x12=1−x12
Find the influence line ordinate of shear at B(SB) for portion CG(12 m<x≤30 m).
Substitute 4−x6 for Dy and x6−3 for Fy in Equation (9).
SB=1−(4−x6)−(x6−3)=1−4+x6−x6+3=−3+0+3=0
Thus, the equations of the influence line ordinate for SB are,
SB=−x12,0≤x<6 m (10)
SB=1−x12,6 m<x<12 m (11)
SB=0,12 m<x≤30 m (12)
Find the influence line ordinate of SB using Equation (10), (11), and (12) and summarize the values in Table 1.
| x (m) | Points | Influence line ordinate of SB(kN/kN) |
| 0 | A | 0 |
| 6 | B− | ‑0.5 |
| 6 | B+ | 0.5 |
| 12 | C | 0 |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
Sketch the influence line diagram for the shear at pointB as shown in Figure 4.

Influence line for moment at point B:
Refer Figure 2.
Find the equation of bending moment at B of portion AB(0≤x<6 m).
Take moment at B.
Consider clockwise moment as positive and anticlockwise moment as negative.
MB=Ay(6)−1(6−x)
Substitute 1−x12 for Ay.
MB=(1−x12)(6)−1(6−x)=6−x2+6+x=x2
Refer Figure 3.
Find the equation of bending moment at B of portion BG(6 m<x≤30 m).
Take moment at B.
Consider clockwise moment as negative and anticlockwise moment as positive.
MB=−1[24−(30−x)]+Dy(12)+Fy(18)=−24+30−x+12Dy+18Fy=6−x+12Dy+18Fy (13)
Find the influence line ordinate of moment at B(MB) for portion BC(6 m<x<12 m).
Substitute x6 for Dy and −x12 for Fy in Equation (13).
MB=6−x+12(x6)+18(−x12)=6−x+2x−3x2=6−x2
Find the influence line ordinate of moment at B (MB) for portion CG(12 m<x≤30 m).
Substitute 4−x6 for Dy and x6−3 for Fy in Equation (13).
MB=−6+x−12(4−x6)−18(x6−3)=−6+x−48+2x−3x+54=0
Thus, the equations of the influence line ordinate for MB are,
MB=x2,0≤x<6 m (14)
MB=6−x2,6 m<x<12 m (15)
MB=0,12 m<x≤30 m (16)
Find the influence line ordinate of MB using Equation (14), (15), and (16) and summarize the values in Table 2.
| x (m) | Points | Influence line ordinate of MB(kN-m/kN) |
| 0 | A | 0 |
| 6 | B | ‑3 |
| 12 | C | 0 |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
Sketch the influence line diagram for the bending moment at point B as shown in Figure 5.
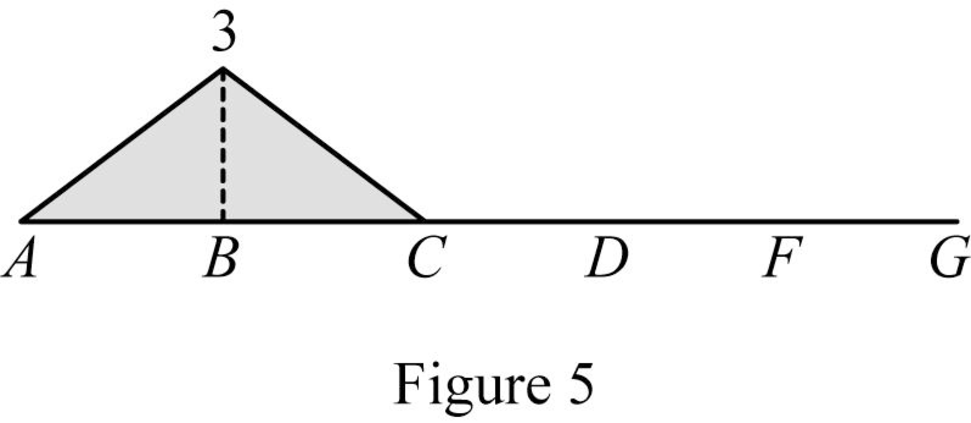
Influence line for shear at hinge C:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of frame as shown in Figure 6.
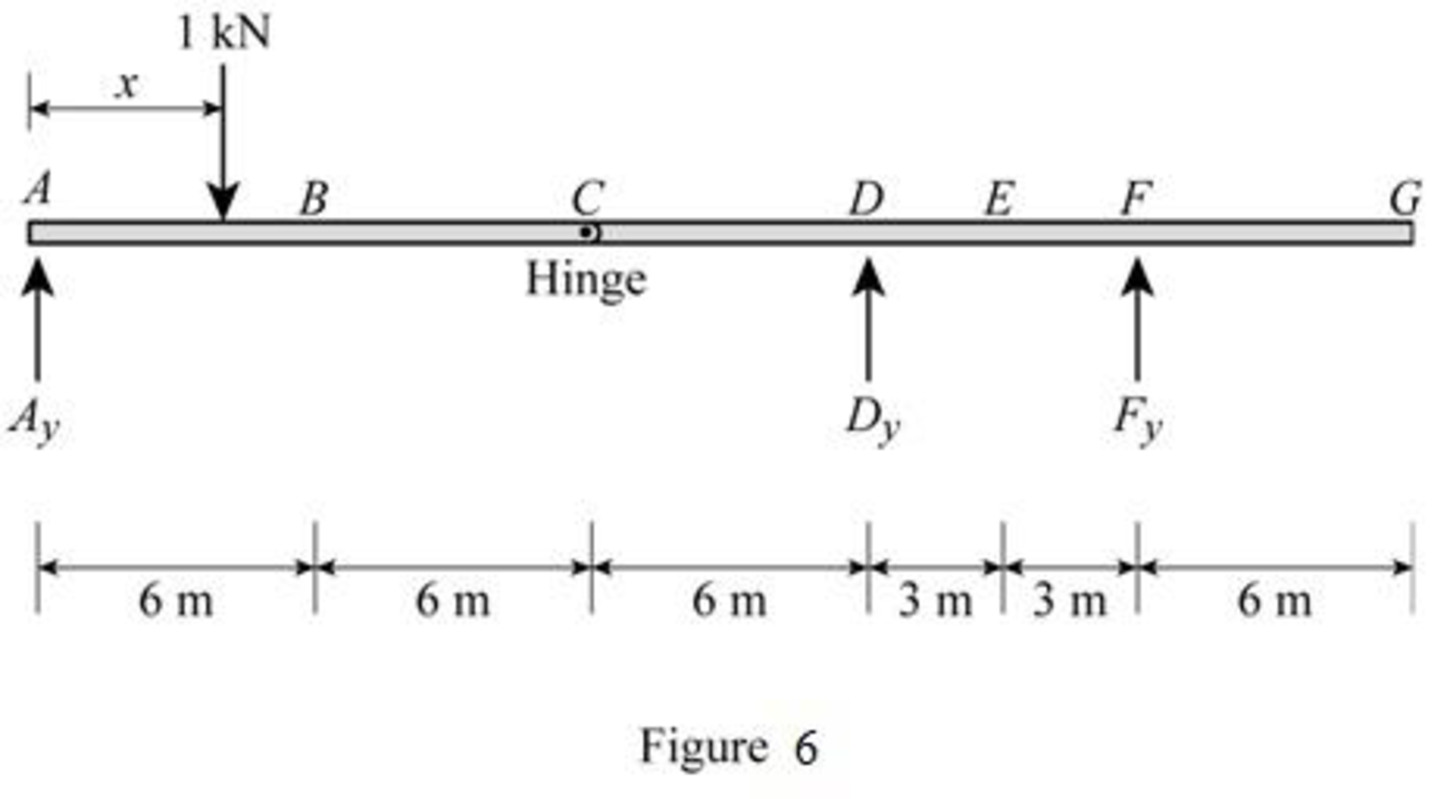
Refer Figure 6.
Consider the unit load at a variable position x to the left hinge C. (placed portion AC of the beam 0≤x<12 m).
Find the vertical support reaction (Ay) at A for portion AC.
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
ΣMACC=0Ay(12)−1(12−x)=012Ay=12−xAy=1−x12
Consider the unit load at a variable position x to the right hinge C. (Place portion CG of the beam 12 m<x≤30 m).
Find the vertical support reaction (Ay) at A for portion CG.
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
ΣMACC=0Ay(12)=0Ay=0
Thus, the equations of the influence line ordinate for Ay are,
Ay=1−x12,0≤x<12 m (17)
Ay=0,12 m<x≤30 m (18)
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction (Dy) using equilibrium equation.
Apply moment equilibrium at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
ΣMF=0Ay(24)+Dy(6)−1(24−x)=06Dy=24−x−24AyDy=4−x6−4Ay (19)
Find the influence line ordinate of vertical reaction (Dy) for portion AC(0≤x<12 m).
Substitute 1−x12 for Ay in Equation (19).
Dy=4−x6−4(1−x12)=4−x6−4+x3=−x+2x6=x6
Find the influence line ordinate of vertical reaction (Dy) for portion CG(12 m<x≤30 m).
Substitute 0 for Ay in Equation (19).
Dy=4−x6−4(0)=4−x6
Thus, the equations of the influence line ordinate for Dy are,
Dy=x6,0≤x<12 m (20)
Dy=4−x6,12 m<x≤30 m (21)
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction (Fy) using force equilibrium equation.
Consider the vertical forces equilibrium condition, take the upward force as positive (↑+) and downward force as negative (↓−).
ΣFy=0Ay+Dy+Fy=1Fy=1−Ay−Dy (22)
Find the influence line ordinate of vertical reaction (Fy) for portion AC(0≤x<12 m).
Substitute 1−x12 for Ay and x6 for Dy in Equation (22).
Fy=1−(1−x12)−(x6)=1−1+x12−x6=−x12
Find the influence line ordinate of vertical reaction (Fy) for portion AC(12 m<x≤30 m).
Substitute 0 for Ay and 4−x6 for Dy in Equation (22).
Fy=1−(0)−(4−x6)=1−4+x6=x6−3
Thus, the equations of the influence line ordinate for Fy are,
Fy=−x12,0≤x<12 m (23)
Fy=x6−3,12 m<x≤30 m (24)
Find the equation of shear at C of portion AC(0≤x<12 m).
Sketch the free body diagram of the section AC as shown in Figure 7.
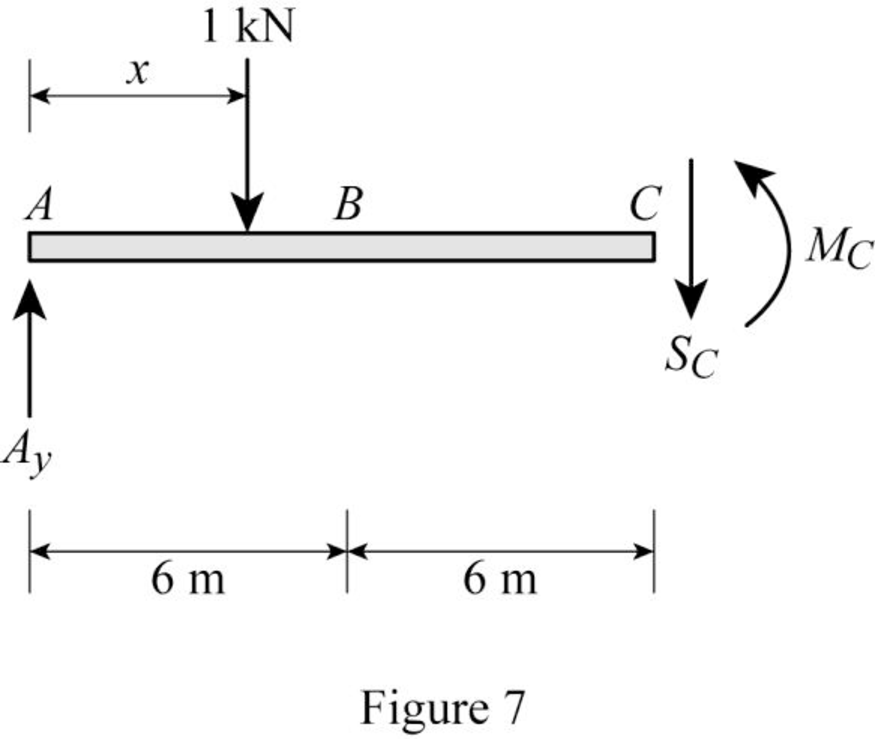
Refer Figure 7.
Apply equilibrium equation of forces.
Consider upward force as positive (↑+) and downward force as negative (↓−).
ΣFy=0
Ay−1−SC=0SC=Ay−1
Substitute 1−x12 for Ay.
SC=(1−x12)−1=−x12
Find the equation of shear at C of portion CG (12 m<x≤30 m).
Sketch the free body diagram of the section CG as shown in Figure 8.
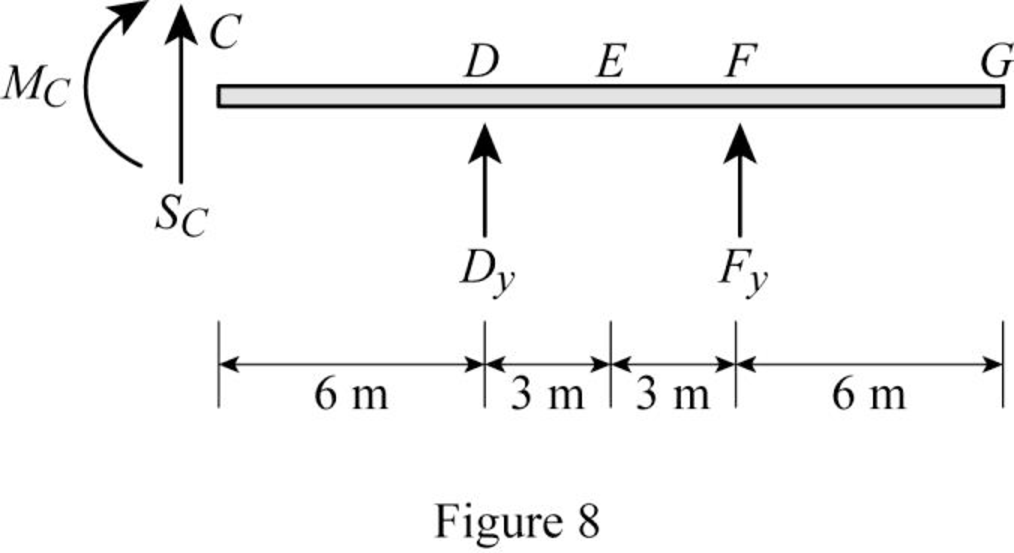
Refer Figure 8.
Apply equilibrium equation of forces.
Consider upward force as positive (↑+) and downward force as negative (↓−).
ΣFy=0
SC−1+Dy+Fy=0SC=1−Dy−Fy (25)
Substitute 4−x6 for Dy and x6−3 for Fy in Equation (25).
SC=1−(4−x6)−(x6−3)=1−4+x6−x6+3=−3+0+3=0
Thus, the equations of the influence line ordinate for SC are,
SC=−x12,0≤x<12 m (26)
SC=0,12 m<x≤30 m (27)
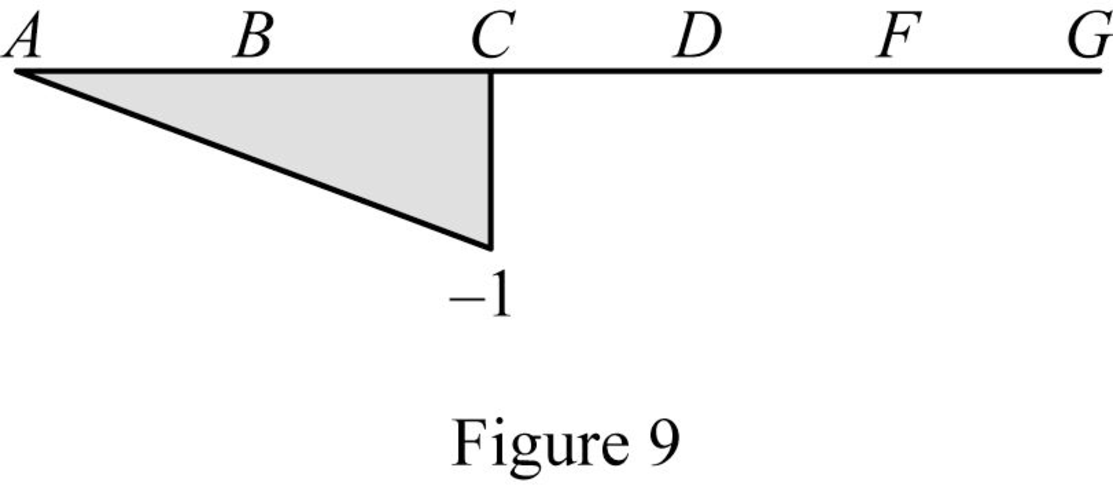
Find the influence line ordinate of SC using Equation (26) and (27) and summarize the values in Table 3.
| x (m) | Points | Influence line ordinate of SC(kN/kN) |
| 0 | A | 0 |
| 6 | B | ‑0.5 |
| 12 | C− | ‑1 |
| 12 | C+ | 0 |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
Sketch the influence line diagram for the shear at point C as shown in Figure 9.
Want to see more full solutions like this?
Chapter 8 Solutions
Structural Analysis
- If you could help me answer these questions in matlab that would be great, I provided an additional picture detailing what the outcome should look like.arrow_forwardA fully grouted reinforced masonry wall is to be constructed of 8-in. CMU. The wall height is 18feet. It is assumed to be simply supported. The wall is to be designed for an out-of-plane seismicload of 52 lbs./ft.2, which can act in either direction. The wall also supports a roof dead load of600 lbs./ft. and a roof live load of 300 lbs./ft. along the wall length. The roof loads have aneccentricity of 2.5 inches. Since there is seismic load, load combinations (6) and (7) in Chapter 2of ASCE 7-22 should be considered. In these two load combinations,horizontal seismic loadhE =andvertical seismic loadvE = . You may ignorevE in this problem for simplicity. The masonryhas a specified compressive strength of 2,500 psi. (a) Use the strength design provisions of TMS402 to determine the size and spacing of the vertical bars needed. Use the P-δ analysis method inSection 9.3.4.4.2 of TMS 402 to determine Mu. (b) Repeat the design using the momentmagnification method in Section 9.3.4.4.3 instead.arrow_forwardThe factor of safety for tipping of the concrete dam is defined as the ratio of the stabilizing moment due to the dam's weight divided by the overturning moment about OO due to the water pressure (Figure 1). Suppose that aa = 5 mm , dd = 2 mm , hh = 7 mm . The concrete has a density of ρconcρconc = 2.5 Mg/m3Mg/m3 and for water ρwρw = 1 Mg/m3Mg/m3arrow_forward
- can you answer both plss, i will give u a likearrow_forward*1-4. The hollow core panel is made from plain stone concrete. Determine the dead weight of the panel. The holes each have a diameter of 100 mm. 200 mm 300 mm 300 mm 300 mm 300 mm 300 mm Prob. 1-4 300 mm 4 marrow_forwardderive the expressions for V and M, and draw the shear forceandbendingmomentdiagrams.Neglecttheweightofthebeam.arrow_forward
- a. Draw trajectories of approximately 8 to 11 vehicles moving on a one way 1-lane road with different time-varying speeds. b. Consider a time-space window in the time-space diagram of part (a). See below. Denote the number of vehicles passing BD, DC, AC, and AB respectively as n1, N2, N3, and n4. Write an equation relating n₁, N2, N3, and n4 to each other. What is the physical intuition of this equation? Please elaborate. X 4 X. n4 n3 с n2 X1 D B n1 t c. Using density (k) definition at time instances t₁ and t₂ and flow (q) definition at locations X1 and X2, rewrite equation of interest in part (b) to demonstrate KAB-KCD 9BD-9AC + t₂-t1 x2-x1 = 0. d. What will be the equation in part (c), in case of x2 → x1 and t₂ → t₁.arrow_forwardConsider a city center where the traffic conditions are described by a Macroscopic Fundamental Diagram (MFD) of network outflow (g- rate of trips finished) vs. accumulation (n- number of cars) with a trapezoidal shape, as shown in the figure below. The values of the parameters are: • • maximum trip completion rate gmax=100 [veh/min] critical accumulations ncr1=1000 [veh] and ncr2=1500 [veh] jam accumulation njam=4000 [veh]. gmax ncr1 ncr2 njam There are two types of demands in the morning peak hour (7-8am): trips generated from outside the city center with rate q1=80 [veh/min], and trips generated from within the city center with rate q2=50 [veh/min]. In addition, a perimeter traffic control, u, is available that only restricts vehicles entering the city from outside. If at 7am there are already no=500 [veh] in the city center: a. Write the dynamic equations (mass conservation equation) in a continuous form for the center of the city. b. Convert the continuous dynamic into the discrete…arrow_forwardAssume a car park facility where the arrival rate is 1 customer every minute, and the service process including pressing the button, taking the card, and waiting for the boom to rise leads to service rate of μ customer every minute. a. Assume the arrival and service processes are stochastic. Using any software (Excel, Matlab, or the one you prefer), plot average delay time (including service time) and average queue size (including the vehicle currently being served) for all combinations of λ = {1,2,3,..,10} and p = {0.1,0.3,0.5,0.7,0.9}. Specifically, we ask you to make 2 graphs (one for average delay and the other for average queue size), where the x-axes contains the different values for 1, and where you make one curve for each p. b. Assume the arrival process is stochastic but the service process is deterministic with rate μ. Using any software (Excel, Matlab, or the one you prefer), plot average delay time (including service time) and average queue size (including the vehicle…arrow_forward
- A traffic signal has a 60-second cycle length (Red time + Green time). For the travel direction of interest, the red and green times are 30 seconds each, the arrival rate is constant at 20 [veh/min] and the saturation flow (i.e., the departure rate) is 1 [veh/sec]. a. Calculate the average delay (for all vehicles) for the travel direction of interest. b. Assume a work zone on the street downstream of the intersection so that only 25 [veh/min] (in the direction of interest) can pass. Calculate the average delay caused by the work zone to a vehicle leaving the intersection. Assume that the queue at the work zone never backs- up into the intersection. c. Discuss qualitatively the implications of queue spillback from the work zone on the delay of the system. Traffic Direction (a) Traffic Direction (b)arrow_forwardAttached pics is a sample problem, can you compute it for me, I just want to compare my answer. Thank you.arrow_forwardProblem 2: The Douglas fir beam below supports uniform live (WL) and dead loads (WD) as shown below. Assume the total distributed load is 700 lb/ft. WD=300#/PT. W₁ = 400# W₁ = 400#/FT- J J J J I J J J L=161 a) Assuming an alllowable deflection of L/360, compute the magnitude of the allowable deflection. b) Using an 8"x12" timber beam (see Table A1-b on page 567 of your text for properties) compute the actual deflection. Assume E = 1.6 x 100 psi. c) Based on your answers for parts a and b, determine if an 8"x12" timber beam is safe for this applicationarrow_forward
