Chapter 7.9, Problem 151P

Solve Prob. 7.150, assuming that the rosette at point A indicates the following strains:

$\in$₁ = −30 × 10−⁶ in./in. $\in$₂ = +250 × 10−⁶ in./in.

$\in$₃ = +100 × 10−⁶ in./in.

7.150 A centric axial force P and a horizontal force Q_x are both applied at point C of the rectangular bar shown. A 45° strain rosette on the surface of the bar at point A indicates the following strains:

$\in$₁ = −60 × 10−⁶ in./in. $\in$₂ = +240 × 10−⁶ in./in.

$\in$₃ = +200 × 10−⁶ in./in.

Knowing that E = 29 × 10⁶ psi and v = 0.30, determine the magnitudes of P and Q_x.

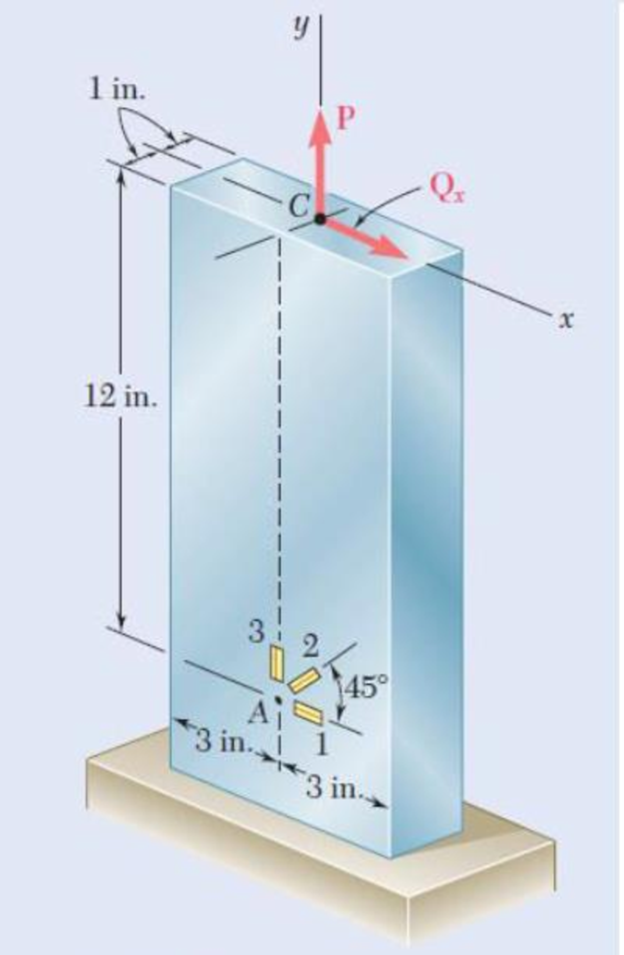
Fig. P7.150