
a.
To find: given proportion,
a.
Answer to Problem 1WE
No, given proportion is not correct.
Explanation of Solution
Given:
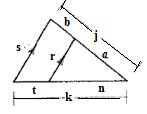
Concept used:
Two
If two triangles are similar then the corresponding sides are in same proportion.
Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
Name the vertices of triangles as A , B and C and the parallel line as D, E.
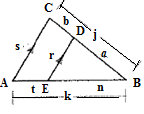
In
is common and
Therefore,
And so
Now if the two triangles are similar then the corresponding sides are in same proportion.
Therefore,
Hence,
b.
To find: given proportion,
b.
Answer to Problem 1WE
yes, given proportion is correct.
Explanation of Solution
Given:
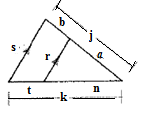
Concept used:
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in same proportion.
If two triangles are similar then the corresponding sides are in same proportion.
Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
Name the vertices of triangles as A , B and C and the parallel line as D, E.
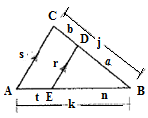
In
Therefore,
And so
Now if the two triangles are similar then the corresponding sides are in same proportion.
Therefore,
Hence,
c.
To find: given proportion,
c.
Answer to Problem 1WE
Yes, given proportion is correct.
Explanation of Solution
Given:
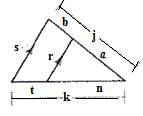
Concept used:
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in same proportion.
If two triangles are similar then the corresponding sides are in same proportion.
Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
Name the vertices of triangles as A , B and C and the parallel line as D, E.
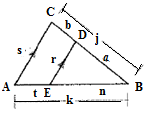
Therefore,
Hence,
d.
To find: given proportion,
d.
Answer to Problem 1WE
No, given proportion is not correct.
Explanation of Solution
Given:
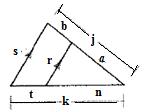
Concept used:
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in same proportion.
If two triangles are similar then the corresponding sides are in same proportion.
Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
Name the vertices of triangles as A , B and C and the parallel line as D, E.
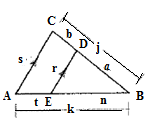
In
Therefore,
And so
Now if the two triangles are similar then the corresponding sides are in same proportion.
Therefore,
Hence,
e.
To find: given proportion,
e.
Answer to Problem 1WE
Yes, given proportion is correct.
Explanation of Solution
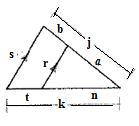
Given:
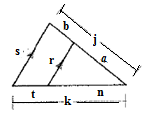
Concept used:
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in same proportion.
If two triangles are similar then the corresponding sides are in same proportion.
Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
Name the vertices of triangles as A , B and C and the parallel line as D, E.
In
Therefore,
And so
Now if the two triangles are similar then the corresponding sides are in same proportion.
Therefore,
Hence,
f.
To find: given proportion,
f.
Answer to Problem 1WE
Yes, given proportion is correct.
Explanation of Solution
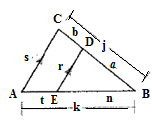
Given:
Concept used:
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in same proportion.
If two triangles are similar then the corresponding sides are in same proportion.
Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
Name the vertices of triangles as A , B and C and the parallel line as D, E.
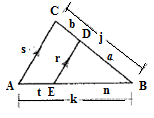
In
Therefore,
And so
Now if the two triangles are similar then the corresponding sides are in same proportion.
Therefore,
We have
And
Which gives,
Hence,
Chapter 7 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Additional Math Textbook Solutions
Elementary Statistics (13th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Introductory Statistics
Algebra and Trigonometry (6th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- 6arrow_forwardDoor 87.5in to 47 living 44.75 Closet 96in Window ISS.Sin 48in Train Table 96in 48in 132:2 Windowarrow_forward39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

