
(a)
The value of
(a)
Answer to Problem 16E
The value of
Explanation of Solution
Given:
The matrices
Concept used:
Operations like addition and subtraction of matrices are only possible when they are of same dimension.
Dimension of matrix with a rows and b columns is given by
If a matrix is multiplied by a scalar then each element of the matrix is multiplied by the same scalar.
Calculation:
Add the matrix A and Bas follows:
Thus, the value of
Now, by graphing utility of matrix capability,
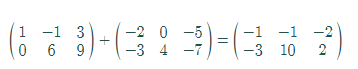
Hence, the result is verified.
(b)
The value of
(b)
Answer to Problem 16E
The value of
Explanation of Solution
Given:
The matrices
Concept used:
Operations like addition and subtraction of matrices are only possible when they are of same dimension.
Dimension of matrix with a rows and b columns is given by
If a matrix is multiplied by a scalar then each element of the matrix is multiplied by the same scalar.
Calculation:
Subtract the matrices A and Bas follows:
Thus, the value of
Now, by graphing utility of matrix capability,

Hence, the result is verified.
(c)
The value of
(c)
Answer to Problem 16E
The value of
Explanation of Solution
Given:
The matrix is
Concept used:
Operations like addition and subtraction of matrices are only possible when they are of same dimension.
Dimension of matrix with a rows and b columns is given by
If a matrix is multiplied by a scalar then each element of the matrix is multiplied by the same scalar.
Calculation:
Multiply all the elements of matrix A by 3 as follows:
Thus, the value of
Now, by graphing utility of matrix capability,
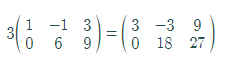
Hence, the result is verified.
(d)
The value of
(d)
Answer to Problem 16E
The value of
Explanation of Solution
Given:
The matrices
Concept used:
Operations like addition and subtraction of matrices are only possible when they are of same dimension.
Dimension of matrix with a rows and b columns is given by
If a matrix is multiplied by a scalar then each element of the matrix is multiplied by the same scalar.
Calculation:
The value of
Thus, the value of
Now, by graphing utility of matrix capability,
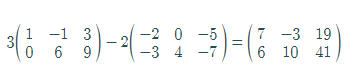
Hence, the result is verified.
Chapter 7 Solutions
PRECALCULUS W/LIMITS:GRAPH.APPROACH(HS)
- 15A cylindrical tank with radius 8 m is being filled with water at a rate of 2 m³/min. What is the rate of change of the water height in this tank? 6)A box with a square base and an open top must box that will minimiarrow_forward#12 The radius of a sphere increases at a rate of 3 in/sec. How fast is the volume increasing when the diameter is 24arrow_forward84 256 cubic inches. Find the dimensions of the of material used (the surface area). A farmer wishes to enclose a rectangular plot using 200 m of fencing material. One side of the land borders a river and does not need fencing. What is the largest area that can be enclosed? For the function y=x³-3x²-1, use derivatives to: 3 b) 2x - 6x2 (a) determine the intarrow_forward
- Can you solve this 6 questions numerical method and teach me how to solve it and what we use.arrow_forward9Wire of length 20m is divided into two pieces and the pieces are bent into a square and a circle. How should this be done in order to minimize the sum of their areas? Round your answer to the nearest hundredth.arrow_forwardUse Laplace transform to solve the initial value problem y' + y = tsin(t), y(0) = 0arrow_forward
- The function g is defined by g(x) = sec² x + tan x. What are all solutions to g(x) = 1 on the interval 0 ≤ x ≤ 2π ? A x = = 0, x == = 3, x = π, x = 7 4 , 4 and x 2π only = B x = 4' 1, x = 1, x = 57 and x = 3 only C x = πk and x = - +πk D , where is any integer П x = +πk and П x = +πk, where k is any integerarrow_forwardVector v = PQ has initial point P (2, 14) and terminal point Q (7, 3). Vector v = RS has initial point R (29, 8) and terminal point S (12, 17). Part A: Write u and v in linear form. Show all necessary work. Part B: Write u and v in trigonometric form. Show all necessary work. Part C: Find 7u − 4v. Show all necessary calculations.arrow_forwardAn object is suspended by two cables attached at a single point. The force applied on one cable has a magnitude of 125 pounds and acts at an angle of 37°. The force on the other cable is 75 pounds at an angle of 150°.Part A: Write each vector in component form. Show all necessary work.Part B: Find the dot product of the vectors. Show all necessary calculations Part C: Use the dot product to find the angle between the cables. Round the answer to the nearest degree. Show all necessary calculations.arrow_forward
- An airplane flies at 500 mph with a direction of 135° relative to the air. The plane experiences a wind that blows 60 mph with a direction of 60°.Part A: Write each of the vectors in linear form. Show all necessary calculations.Part B: Find the sum of the vectors. Show all necessary calculations. Part C: Find the true speed and direction of the airplane. Round the speed to the thousandths place and the direction to the nearest degree. Show all necessary calculations.arrow_forwardUse sigma notation to write the sum. Σ EM i=1 - n 2 4n + n narrow_forwardVectors t = 3i + 7j, u = 2i − 5j, and v = −21i + 9j are given.Part A: Find the angle between vectors t and u. Show all necessary calculations. Part B: Choose a value for c, such that c > 1. Find w = cv. Show all necessary work.Part C: Use the dot product to determine if t and w are parallel, orthogonal, or neither. Justify your answer.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





