
Concept explainers
(a)
To Find: To find a quadratic model and a linear model for yearly revenues of the given travel companies.
(a)
Explanation of Solution
Given information:Yearly revenues of both the online travel companies.
Since x represent the year with
Let
| 2 | 4.03 | 5.26 |
| 3 | 4.77 | 6.79 |
| 4 | 5.76 | 8.44 |
| 5 | 6.67 | 9.22 |
| 6 | 8.77 | 10.74 |
| 7 | 10.06 | 12.68 |
Using the graphing utility, with regression feature the quadratic model for the first company came to be
(b)
To Graph: Tograph the given model functions
(b)
Explanation of Solution
Given information:Given model functions are
Graph:
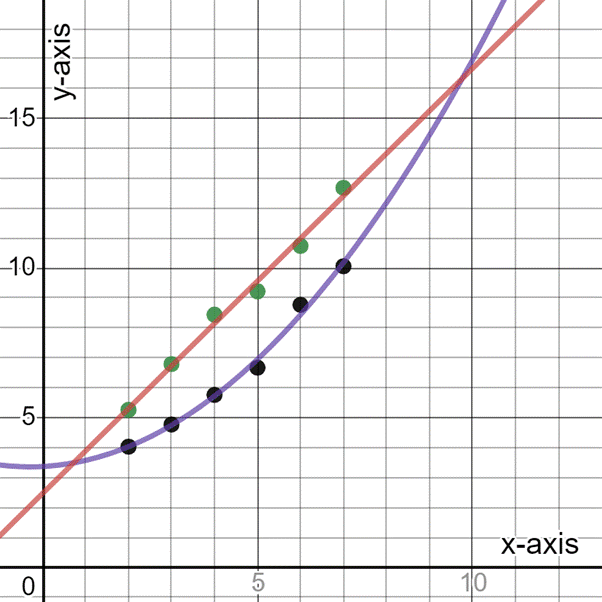
Interpretation:
From the graph, the x-axis shows the year x and y-axis shows yearly revenue.
The red line represents the given linear model whereas the blue line represents the given quadratic model with original scatter points.
(c)
To Find: Tofind the year in which the revenue of second company is greater then first company.
(c)
Answer to Problem 90E
The answer is from 2011.
Explanation of Solution
Given information:Given model functions are
From the graph, it can be seen that in the year 2011 the revenue of second company exceeds the first company and it continues till 2019.
(d)
To Find: To find the solutions of the given model functions.
(d)
Answer to Problem 90E
The answer is
Explanation of Solution
Given information:Given model functions are
Formula used: Substitution method
Calculation:
The point of intersection find out when
Using
Thus, the value of x is approximately 10 and 1.
Since
Therefore
Hence, the revenue exceeds first in the year of 2011.
(e)
To Compare: To compare the above results.
(e)
Explanation of Solution
Given information:Given model functions are
By comparing the above results, both methods gives the same results
Chapter 7 Solutions
PRECALCULUS W/LIMITS:GRAPH.APPROACH(HS)
- Find the Soultion to the following dy differential equation using Fourier in transforms: = , хуо, ухо according to the terms: lim u(x,y) = 0 x18 lim 4x (x,y) = 0 x14 2 u (x, 0) = =\u(o,y) = -y لوarrow_forwardCan you solve question 3,4,5 and 6 for this questionarrow_forwardwater at a rate of 2 m³/min. of the water height in this tank? 16) A box with a square base and an open top must have a volume of 256 cubic inches. Find the dimensions of the box that will minimize the amount of material used (the surface area). 17) A farmer wishes toarrow_forward
- #14 Sand pours from a chute and forms a conical pile whose height is always equal to its base diameter. The height o the pile increases at a rate of 5 feet/hour. Find the rate of change of the volume of the sand in the conical pile when the height of the pile is 4 feet.arrow_forward(d)(65in(x)-5 cos(x) dx mins by 5x-2x² 3x+1 dx -dx 20 Evaluate each the following indefinite integralsarrow_forward19 Evaluate each the following definite integrals: a) લ b) (+3) 6) (2-2)(+33) dxarrow_forward
- #11 If a snowball melts so its surface area decreases at a rate of 1cm²/min, find the rate at which the diameter decreases when the diameter is 6 cm.arrow_forwardUse Deritivitve of the inverse to solve thisarrow_forwardEvaluate the following Limits: e6x-1 Lim +0Sin3x 7x-5x2 2x-1+ Cos 4x +6 c) Lim b) Lim + x³-x2 X-0 1-e' 4x d) Lim 6x²-3 X+0 6x+2x² Find the derivatives of the following functions using the Limit definition of derivativearrow_forward
- 15A cylindrical tank with radius 8 m is being filled with water at a rate of 2 m³/min. What is the rate of change of the water height in this tank? 6)A box with a square base and an open top must box that will minimiarrow_forward#12 The radius of a sphere increases at a rate of 3 in/sec. How fast is the volume increasing when the diameter is 24arrow_forward84 256 cubic inches. Find the dimensions of the of material used (the surface area). A farmer wishes to enclose a rectangular plot using 200 m of fencing material. One side of the land borders a river and does not need fencing. What is the largest area that can be enclosed? For the function y=x³-3x²-1, use derivatives to: 3 b) 2x - 6x2 (a) determine the intarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





