
Using the property indicated in Prob. 7.124, determine the curve assumed by a cable of span L and sag h carrying a distributed load w = w0 cos (πx/L), where x is measured from mid-span. Also determine the maximum and minimum values of the tension in the cable.
PROBLEM 7.124 Show that the curve assumed by a cable that carries a distributed load w(x) is defined by the differential equation d2y/dx2 = w(x)/T0, where T0 is the tension at the lowest point.
The expression for the curve made by the cable, maximum and minimum values of the tension in the cable.
Answer to Problem 7.125P
The curve represented by the cable is
Explanation of Solution
The figure 1 below shows the cable and which makes the curve due the load w.
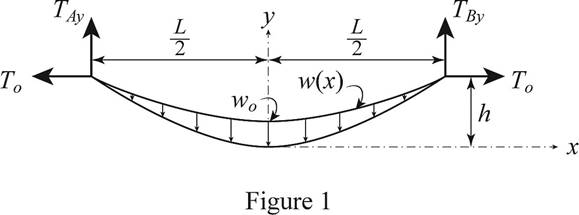
Write the expression for the load distributed.
Refer the problem 77268-7.4-7.124P and writhe the differential equation for the curve.
Write the expression for the differential equation for the curve.
Substitute
Integrate both side of the above equation and apply the condition
Integrate the above equation and apply the condition
Here C is the integration constant.
Apply the condition
Substitute
At
Substitute
The value of y at
Rewrite the above equation in terms of h.
Here
Therefore the minimum tension on the cable is
To find the maximum tension on the cable the slope of the above equation for y at
Here
Substitute
Rewrite the above equation in terms of
Write the expression to calculate the maximum tension on the cable.
Here
Substitute
Conclusion:
Thus, the curve represented by the cable is
Want to see more full solutions like this?
Chapter 7 Solutions
EBK VECTOR MECHANICS FOR ENGINEERS: STA
- reading is 0.4 mas SHOWN. Assume h₁ = 0.4 m, h₂ = 0.5 m. (a) Do you know the specific weight of mercury? (b) Do you know the specific weight of gasoline? (c) Do you know the specific weight of oil? (a) YHg = 133,000 (b) Ygas = 6867 (c) Yoil = 8829 eTextbook and Media Part 2 N/m³ N/m³ N/m³ A+ Gasoline t +B Oil -Mercury Attempts: unlimited Did you calculate the pressure difference between two locations using the correct specific weight? Did you assume that the pressures in fluid are the same in a horizontal plane even though they are in different tubes? Are the calculated pressures in a column of fluid always higher at lower elevations? Did you account for the fact that the two horizontal tubes of the U-tube are above the ground? Concepts: The pressure in a fluid is a function of the specific weight of the fluid and the height relative to a reference. Pressure is constant in a horizontal plane of a continuous mass of fluid. (a) What is the initial pressure difference? (PA-PB) (b) What is…arrow_forwardFind the solution of the following Differential Equations 1) "-4y+3y=0 3) "+16y=0 2) y"-16y=0 4) y"-y-6y=0 5) y"+2y=0 7) y"+y=0, (#0) 9) y"-y=0, y(0) = 6, y'(0) = -4 11) y"-4y+3y=0, y(0)=-1, 13) y'(0) = -5 "+2y+2y=0 15) y"-9y=0 17) y"-4y=0 6) y"-2y+2y=0 8) "+4y+5y=0 10) y"-9y=0, y(0) = 2, y'(0) = 0 12) y"-3y+2y= 0, y(0)=-1, y'(0) = 0 14) 4y+4y+y=0 16) "+6y+12y=0 18) 4y+4y+17y=0arrow_forwardAccess Pearson Mastering Engineering Back to my courses Course Home Course Home Scoresarrow_forward
- Access Pearson Mastering Engineering Back to my courses Course Home Course Home Scores Review Next >arrow_forwardAccess Pearson Course Home Scoresarrow_forwardAccess Pearson Mastering Engineering Back to my courses Course Home Course Home Scoresarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





