Chapter 7.3, Problem 7.87P

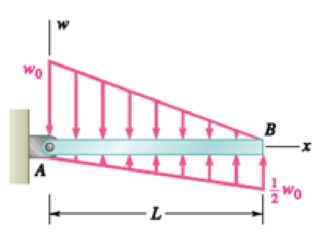
For the beam and loading shown, (a) write the equations of the shear and bending-moment curves, (b) determine the magnitude and location of the maximum bending moment.

To determine

To write the equations of the shear and bending moment curves.

Answer to Problem 7.87P

The equation for shear curve is $V=\frac{1}{4}{\omega }_{0}L\left[3{\left(\frac{x}{L}\right)}^2-4\left(\frac{x}{L}\right)+1\right]$ and the equation for bending moment curve is $M=\frac{1}{4}{\omega }_0{L}^2\left[{\left(\frac{x}{L}\right)}^3-2{\left(\frac{x}{L}\right)}^2+\left(\frac{x}{L}\right)\right]$.

Explanation of Solution

Refer Fig P7.87.

Write the equation for the distributed load.

$\begin{array}{c}w=w_0\left(1-\frac{x}{L}\right)-\frac{w_0}{2}\left(\frac{x}{L}\right)\\ =w_0\left(1-\frac{3x}{2L}\right)\end{array}$ (I)

Here, $w_0$ is the initial load, $w$ is the load, and $L$ is the length of the load.

Write the equation for change in shear moment with distance.

$\frac{dV}{dx}=-w$ (II)

Here, $V$ is the shear moment.

Write the equation for change in bending moment with distance.

$\frac{dM}{dx}=V$ (III)

Here, $M$ is the bending moment.

Conclusion:

Calculate the change in shear moment with distance using equation (II) and thus, find the equation for the shear moment curve.

$\begin{array}{c}\frac{dV}{dx}=-w\\ =-w_0\left(1-\frac{3x}{2L}\right)\\ V=-{\displaystyle \int w_0\left(1-\frac{3x}{2L}\right)dx}\\ =-w_0\left(x-\frac{3x^2}{4L}\right)+C_1\end{array}$ (IV)

Calculate the change in bending moment with distance using equation (III) and thus find the equation for the bending moment curve.

$\begin{array}{c}\frac{dM}{dx}=V\\ M={\displaystyle \int Vdx}\\ ={\displaystyle \int \left(-w_{0}x+\frac{3}{4}{w}_0\frac{x^2}{L}+\frac{1}{4}{w}_{0}L\right)dx}\\ =-\frac{1}{2}{w}_0{x}^2+\frac{1}{4}{w}_0\frac{x^3}{L}+\frac{1}{4}{w}_{0}Lx+C_2\end{array}$ (V)

Apply boundary condition to find $C_1$.

At $x=L$

$\begin{array}{c}V=0\\ -w_0\left(x-\frac{3x^2}{4L}\right)+C_1=0\\ C_1=\frac{1}{4}{w}_{0}L\end{array}$ (V)

Apply boundary condition to find $C_2$.

At $x=0$

$M=C_2=0$ (VI)

Use equation (V) to find the equation for shear curve.

$V=\frac{1}{4}{\omega }_{0}L\left[3{\left(\frac{x}{L}\right)}^2-4\left(\frac{x}{L}\right)+1\right]$

Use equation (VI) to find the equation for bending moment curve.

$M=\frac{1}{4}{\omega }_0{L}^2\left[{\left(\frac{x}{L}\right)}^3-2{\left(\frac{x}{L}\right)}^2+\left(\frac{x}{L}\right)\right]$

Therefore, the equation for shear curve is $V=\frac{1}{4}{\omega }_{0}L\left[3{\left(\frac{x}{L}\right)}^2-4\left(\frac{x}{L}\right)+1\right]$ and the equation for bending moment curve is $M=\frac{1}{4}{\omega }_0{L}^2\left[{\left(\frac{x}{L}\right)}^3-2{\left(\frac{x}{L}\right)}^2+\left(\frac{x}{L}\right)\right]$.

To determine

The magnitude and location of the maximum bending moment.

Answer to Problem 7.87P

The magnitude of the maximum bending moment is $\frac{1}{27}{w}_0{L}^2$ and the location is at $x=\frac{L}{3}$.

Explanation of Solution

The maximum absolute value of the bending moment can be found using the equation for the bending moment curve.

Write the equation to find the maximum bending moment.

$\frac{dM}{dx}=V=0$

Conclusion:

Calculate the location of the maximum bending moment.

$\begin{array}{c}\frac{dM}{dx}=V=0\\ 0=\left[3{\left(\frac{x}{L}\right)}^2-4\left(\frac{x}{L}\right)+1\right]\\ =\left(3\frac{x}{L}-1\right)\left(\frac{x}{L}-1\right)\\ x=\frac{L}{3}\text{and }x=L\end{array}$ (VI)

Calculate the maximum bending moment.

$\begin{array}{c}{M}_{\max }=\frac{1}{4}{w}_0{L}^2\left(\frac{1}{27}-\frac{2}{9}+\frac{1}{3}\right)\\ =\frac{1}{27}{w}_0{L}^2\end{array}$ (VI)

Therefore, the magnitude of the maximum bending moment is $\frac{1}{27}{w}_0{L}^2$ and the location is at $x=\frac{L}{3}$.