Chapter 7.4, Problem 2AYU

To determine

Trigonometric identity in the form sin�(-θ )+cos�(-θ)= cos�θ-sin�θ exists

Answer to Problem 2AYU

Solution:

True.Trigonometric identity in the form sin�(-θ )+cos�(-θ)= cos�θ-sin�θ exists.

Explanation of Solution

:

Given:

Trigonometric identity is in the form of sin�(-θ )+cos�(-θ)= cos�θ-sin�θ

Calculation:

Consider a unit circle.

Equation of a unit circle = x²+ y² =1. -------1

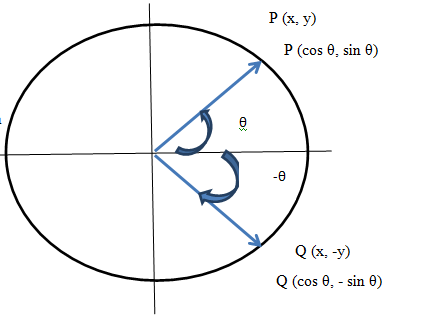
If P (x, y) is a point on the unit circle that corresponds to angle θ then

y = sin θ, x = cos θ. ------2

Using the symmetry, the point Q on the unit circle corresponds to the angle (-θ).

The point Q has the coordinates (x, -y).

Using values from equation 2 to obtain the coordinates of Q

Q(x, -y) = Q (cos θ, -sin θ). ---3

By definition of trigonometric function

Coordinate of Q is formed as

sin�(-θ)= -y

cos�(-θ)= x

Using the coordinates of Q from

Equation3

sin�(-θ )+cos�(-θ)=

-sin�(θ )+cos�θ

  

Rearranging

sin�(-θ )+cos�(-θ)= cos�θ- sin�θ