Chapter 7.2, Problem 80AYU

Problems 79 and 80 require the following discussion: When granular materials are allowed to fall freely, they form conical (cone-shaped) piles. The naturally occurring angle of slope, measured from the horizontal, at which the loose material comes to rest is called the angle of repose and varies for different materials. The angle of repose $\theta$ is related to the height $h$ and base radius $r$ of the conical pile by the equation $\theta ={\cot }^{-1}\frac{r}{h}$. See the illustration.

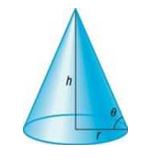
Angle of Repose: Bunker Sand The steepness of sand bunkers on a golf course is affected by the angle of repose of the sand (a larger angle of repose allows for steeper bunkers). A freestanding pile of loose sand from a United States Golf Association (USGA) bunker had a height of 4 feet and a base diameter of approximately $\text{6}\text{.68}$ feet.

(a) Find the angle of repose for USGA bunker sand.

(b) What is the height of such a pile if the diameter of the base is 8 feet?

(c) A 6-foot-high pile of loose Tour Grade 50/50 sand has a base diameter of approximately $\text{8}\text{.44}$ feet. Which type of sand (USGA or Tour Grade 50/50) would be better suited for steep bunkers?

To determine

To find:

A. The angle of repose $\theta$ for USGA bunker sand.

Answer to Problem 80AYU

Solution:

A. The angle of repose $\theta$ for the USGA bunker sand $={\text{ cot}}^{-1}\left(r/h\right)\approx 50.13°$.

Explanation of Solution

Given:

Height of the freestanding pile of loose sand from USGA bunker $=h=4\text{ feet}$.

Base diameter of the freestanding pile of loose sand from USGA bunker $\left(D\right)\approx 6.68\text{ feet}$.

Radius of the freestanding pile of loose sand from USGA bunker $\left(r\right)\approx 6.68/2\text{ feet }=3.34\text{ feet}$.

Formula used:

The angle of repose $\theta ={\text{ cot}}^{-1}\left(r/h\right)\text{, }0<\theta <\pi$.

Calculation:

To find $\theta$, we need to find cos $\theta$, because $y={\text{ cos}}^{-1}x$ has the same range as $y={\text{ cot}}^{-1}x$ except where undefined.

The angle of repose $\theta ={\text{ cot}}^{-1}\left(3.34\right)/4),0<\theta <\pi$.

$\theta ={\text{ cot}}^{-1}\left(3.34/4\right),0<\theta <\pi$

$\theta ={\text{ cot}}^{-1}\left(3.34/4\right)={\text{ cot}}^{-1}\left(x/y\right)$

Here, $x=3.34,y=4$.

Both $x$ and $y$ are positive, therefore $\theta$ lies in the I quadrant.

Equation of the circle $=x^2+y^2 =R^2$.

Where $R=\text{ radius of the circle}$.

$R=\surd \left(x^2+y^2\right)=\surd \left({3.34}^2+4^2\right)=\surd \left({11.15}^2+16\right)=\surd 27.15=5.21\text{ feet}$

Using the formula,

$\text{cos}\theta =x/R$

$\text{cos}\theta =3.34/5.210<\theta <\pi /2\left(\text{I quadrant}\right)$

${\text{cot}}^{-1}\left(3.34/4\right)=\theta ={\text{ cos}}^{-1}\left(3.34/5.21\right)$

${\text{cos}}^{-1}\left(0.641\right)\approx 50.13°={0.874}^c$

The angle of repose θ for the USGA bunker sand $={\text{ cot}}^{-1}\left(r/h\right)={\text{ cot}}^{-1}\left(3.34/4\right)\approx 50.13°$.

To determine

To find:

b. The height of conical USGA bunker sand pile.

Answer to Problem 80AYU

Solution:

b. The height of conical USGA bunker sand pile $h=4.78\text{ feet} \approx 5\text{ feet}$.

Explanation of Solution

Given:

The base diameter of conical pile $=8\text{ feet}$.

Radius of the conical pile $=4\text{ feet}$.

From 80 (a),

Angle of repose $\Theta =50.13°$.

Formula used:

$\Theta ={\text{ cot}}^{-1}\left(r/h\right)$

$\text{cot}\theta =r/h$

Calculation:

$\text{cot}50.13°=4/h$

Using the formula,

$\text{cot}\theta =1/\text{tan}\theta$

$\text{tan}\left(50.13°\right)=h/4$

$h=4\text{ x tan}\left(50.13°\right)$

$h=4\text{ x }1.197=4.78\text{ feet} \approx 5\text{ feet}$

Height of conical sand pile $\approx 5\text{ feet}$.

To determine

To find:

c. If USGA sand pile or tour grade $50/50$ sand is better choice for steep bunkers.

Answer to Problem 80AYU

Solution:

Angle of repose for tour grade $50/50$ sand is higher than USGA sand pile.

Tour grade $50/50$ sand is better choice for steep bunkers than USGA sand pile.

Explanation of Solution

Given:

The height of the conical Tour grade $50/50$ sand pile $h=6\text{ feet}$.

Base diameter of conical Tour grade $50/50$ sand pile $D=8.44\text{ feet}$.

Base radius of conical Tour grade $50/50$ sand pile $=r=8.44/2\text{ feet }=4.22\text{ feet}$.

Formula used:

The angle of repose $\theta ={\text{ cot}}^{-1}\left(r/h\right)$.

Calculation:

To find $\theta$, we need to find cos $\theta$, because $y={\text{ cos}}^{-1}x$ has the same range as $y={\text{ cot}}^{-1}x$ except where undefined.

The angle of repose $\theta ={\text{ cot}}^{-1}\left(4.22/6\right),0<\theta <\pi$.

$\theta ={\text{ cot}}^{-1}\left(4.22/6\right),0<\theta <\pi$

$\theta ={\text{ cot}}^{-1}\left(4.22/6\right)={\text{ cot}}^{-1}\left(x/y\right)$

Here, $x=4.22,y=6$.

Both $x$ and $y$ are positive, therefore $\theta$ lies in the I quadrant.

Equation of the circle $=x^2+y^2 =R^2$.

Where $R=\text{ radius of the circle}$.

$R=\surd \left(x^2+y^2\right)=\surd \left({4.22}^2+6^2\right)=\surd \left({17.80}^2+36\right)=\surd 53.80=7.33\text{ feet}$

Using the formula,

$\text{cos}\theta =x/R$

$\text{cos}\theta =4.22/7.33 0<\theta <\pi /2 \left(\text{I quadrant}\right)$

${\text{cot}}^{-1}\left(4.22/6\right)=\theta ={\text{ cos}}^{-1}\left(4.22/7.33\right)$

${\text{cos}}^{-1}\left(0.575\right)\approx 54.9°={0.958}^c$

The angle of repose $\theta$ for the tour grade $50/50$ sand $={\text{ cot}}^{-1}\left(r/h\right)={\text{ cot}}^{-1}\left(4.22/6\right)\approx 54.9°$.

The angle of repose $\theta$ for the USGA bunker sand $={\text{ cot}}^{-1}\left(r/h\right)={\text{ cot}}^{-1}\left(3.34/4\right)\approx 50.13°$.

Angle of repose for tour grade $50/50$ sand is higher than USGA sand pile.

Tour grade $50/50$ sand is better choice for steep bunkers than USGA sand pile.