
(a)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.
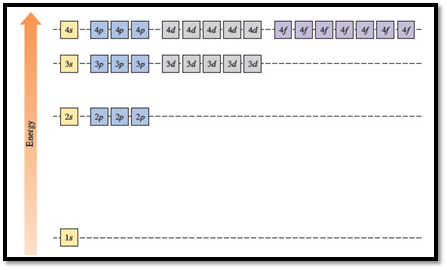
Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in
To find: Identify the orbital which is higher in energy in the given pair 1s, 2s orbitals of hydrogen.
Find the value of ‘n’
(b)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 2p, 3p orbitals of hydrogen
Find the value of ‘n’
(c)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 3dxy, 3dyz orbitals of hydrogen
Find the value of ‘n’
(d)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 3s, 3d orbitals of hydrogen
Find the value of ‘n’
(e)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 4f, 5s orbitals of hydrogen
Find the value of ‘n’
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
EBK GENERAL CHEMISTRY: THE ESSENTIAL CO
- X 5 Check the box under each molecule that has a total of five ẞ hydrogens. If none of the molecules fit this description, check the box underneath the table. CI Br Br Br 0 None of these molecules have a total of five ẞ hydrogens. Explanation Check esc F1 F2 tab caps lock fn Q @2 A W # 3 OH O OH HO © 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Center | Accessibility IK F7 F7 F8 TA F9 F10 & 6 28 * ( > 7 8 9 0 80 F3 O F4 KKO F5 F6 S 64 $ D % 25 R T Y U பட F G H O J K L Z X C V B N M H control option command P H F11 F12 + || { [ command optionarrow_forwardAn open vessel containing water stands in a laboratory measuring 5.0 m x 5.0 m x 3.0 m at 25 °C ; the vapor pressure (vp) of water at this temperature is 3.2 kPa. When the system has come to equilibrium, what mass of water will be found in the air if there is no ventilation? Repeat the calculation for open vessels containing benzene (vp = 13.1 kPa) and mercury (vp = 0.23 Pa)arrow_forwardEvery chemist knows to ‘add acid to water with constant stirring’ when diluting a concentrated acid in order to keep the solution from spewing boiling acid all over the place. Explain how this one fact is enough to prove that strong acids and water do not form ideal solutions.arrow_forward
- The predominant components of our atmosphere are N₂, O₂, and Ar in the following mole fractions: χN2 = 0.780, χO2 = 0.21, χAr = 0.01. Assuming that these molecules act as ideal gases, calculate ΔGmix, ΔSmix, and ΔHmix when the total pressure is 1 bar and the temperature is 300 K.arrow_forwarddG = Vdp - SdT + μA dnA + μB dnB + ... so that under constant pressure and temperature conditions, the chemical potential of a component is the rate of change of the Gibbs energy of the system with respect to changing composition, μJ = (∂G / ∂nJ)p,T,n' Using first principles prove that under conditions of constant volume and temperature, the chemical potential is a measure of the partial molar Helmholtz energy (μJ = (∂A / ∂nJ)V,T,n')arrow_forwardThe vapor pressure of dichloromethane at 20.0 °C is 58.0 kPa and its enthalpy of vaporization is 32.7 kJ/mol. Estimate the temperature at which its vapor pressure is 66.0 kPa.arrow_forward
- Draw the structure of A, the minor E1 product of the reaction. Cl Skip Part Check F1 esc CH_CH OH, D 3 2 Click and drag to start drawing a structure. 80 R3 F4 F2 F3 @ 2 # $ 4 3 Q W 95 % KO 5 F6 A F7 × G ☐ Save For Later Sub 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy C ►II A A F8 F9 F10 FL 6 7 88 & * 8 9 LLI E R T Y U A S D lock LL F G H 0 P J K L Z X C V B N M 9 Harrow_forwardFrom the choices given, which two substances have the same crystal structure? (Select both) Group of answer choices ZnS (zincblende) Diamond TiO2 (rutile) ZnS (wurtzite)arrow_forwardPotassium (K) blends with germanium (Ge) to form a Zintl phase with a chemical formula of K4Ge4. Which of the following elements would you expect potassium to blend with to form an alloy? Electronegativities: As (2.0), Cl (3.0), Ge (1.8), K (0.8), S (2.5), Ti (1.5) Group of answer choices Arsenic (As) Sulfur (S) Chlorine (Cl) Titanium (Ti)arrow_forward
- Consider two elements, X and Z. Both have cubic-based unit cells with the same edge lengths. X has a bcc unit cell while Z has a fcc unit cell. Which of the following statements is TRUE? Group of answer choices Z has a larger density than X X has more particles in its unit cell than Z does X has a larger density than Z Z has a larger unit cell volume than Xarrow_forwardHow many particles does a face-centered cubic (fcc) unit cell contain? Group of answer choices 2 14 8 4arrow_forwardV Highlight all of the carbon atoms that have at least one beta (B) hydrogen, using red for one ẞ hydrogen, blue for two ẞ hydrogens, and green for three ẞ hydrogens. If none of the carbon atoms have ẞ hydrogens, check the box underneath the molecule. ED X None of the carbon atoms have ẞ hydrogens. Explanation esc 2 Check * F1 F2 1 2 80 # 3 Q W tab A caps lock shift fn control F3 N S option O 694 $ F4 F5 F6 005 % E R D F LL 6 olo 18 Ar B © 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Center | Accessibility A DII F7 F8 87 & * 8 T Y U G H 4 F9 F10 ( 9 0 E F11 F12 உ J K L + || X C V B N M H H command option commandarrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





