
To graph: The back-to-back stem plot to represent the school performance, on the basis of grade point average (GPA) and a standardized test (IQ) of 78 seventh-grade student.
Explanation of Solution
Graph: The back-to-back stem plot is useful to compare the two related distributions by having the same stem and two leaves.
For the grade point average (GPA) of 78 seventh-grade student, draw back-to-back stemplot. The values on the left side represent the women scores and the values on the right side represent the men score. The back-to-back stemplot for comparing the distributions is shown below:
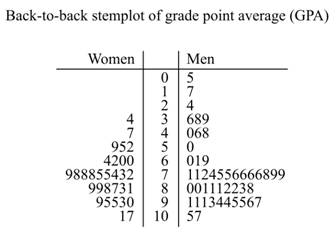
For a standardized test (IQ) of 78 seventh-grade student, draw back-to-back stemplot. The values on the left side represent the women scores and the values on the right side represent the men score. The back-to-back stemplot for comparing the distributions is shown below:
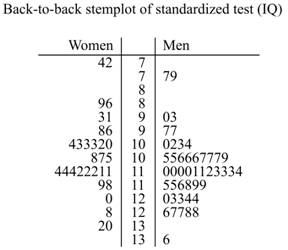
Interpretation: From the above graphs, it can be concluded that the distribution for the grade point average (GPA) and a standardized test (IQ) of 78 seventh-grade student appears almost similar.
To test: The significance difference for the grade point average (GPA) and a standardized test (IQ) of 78 seventh-grade student on the basis of gender.
Answer to Problem 143E
Solution: The difference is insignificant for the grade point average (GPA) scores of men and women. For a standardized test (IQ), the difference is insignificant as the test results are strongly significant.
Explanation of Solution
Calculation: For the difference in grade point average (GPA), the testing can be done as shown below:
The null hypothesis assumes that on an average there is no significant difference on the grade point average (GPA) scores of men and women while the alternative hypothesis assumes that on an average the grade point average (GPA) scores of men is less than the women. Symbolically, the hypothesis can be represented as follows,
Where,
To test the significant difference for the grade point averages, perform the following steps in Minitab,
Step 1: Enter the data in the worksheet of Minitab.
Step 2: Sort the data for ‘GPA’ on the basis of ‘Gender’. Here, ‘2’ represent the men and ‘1’ represent the women. Go to Data, click on sort, select ‘GPA’ in the ‘Sort column’ and enter ‘Gender’ in the ‘By column’ textbox. Also, store sorted data in the column of current worksheet. After this, make two columns, one for ‘GPA (M)’and other one for ‘GPA (F)’.
Step 3: In a Minitab worksheet go to ‘Stat’ point on ‘Basic Statistics’ and click on ‘2-Sample t’.
Step 4: In the dialogue box that appears select the samples in different column and enter the variable ‘GPA (M)’ in the first textbox and the variable ‘GPA (F)’ in the second textbox.
Step 5: Next click on options tab and set the confidence level as 95 and the Alternative hypothesis as ‘less than’. Finally click on OK twice to obtain the output.
From the Minitab results, the test statistic value is obtained as
For the difference in the standardized test (IQ) scores, the testing can be done as shown below:
The null hypothesis assumes that on an average there is no significant difference between the standardized test (IQ) scores of men and women while the alternative hypothesis assumes that on an average the standardized test (IQ) scores of men is greater than the women. Symbolically, the hypothesis can be represented as follows,
Where,
To test the significant difference for the standardized test (IQ) scores, perform the following steps in Minitab,
Step 1: Enter the data in the worksheet of Minitab.
Step 2: Sort the data for ‘IQ’ on the basis of ‘Gender’. Here, ‘2’ represent the men and ‘1’ represent the women. Go to Data, click on sort, select ‘IQ’ in the ‘Sort column’ and enter ‘Gender’ in the ‘By column’ textbox. Also, store sorted data in the column of current worksheet. After this, make two columns, one for ‘IQ (M)’and other one for ‘IQ (F)’.
Step 3: In a Minitab worksheet go to ‘Stat’ point on ‘Basic Statistics’ and click on ‘2-Sample t’.
Step 4: In the dialogue box that appears select the samples in different column and enter the variable ‘IQ (M)’ in the first textbox and the variable ‘IQ (F)’ in the second textbox.
Step 5: Next click on options tab and set the confidence level as 95 and the Alternative hypothesis as ‘greater than’. Finally click on OK twice to obtain the output.
From the Minitab results, the test statistic value is obtained as
Conclusion: Hence, for the grade point average (GPA), the P-value is greater than 0.05, so at 5% level of significance the null hypothesis will be accepted and it is concluded that the difference is insignificant. For the standardized test (IQ) scores, the P-value is greater than 0.05, so at 5% level of significance, the null hypothesis will be accepted and it is concluded that the difference is insignificant.
To find: The 95% confidence intervals for the grade point average (GPA) and the standardized test (IQ) scores of 78 seventh-grade student on the basis of gender.
Answer to Problem 143E
Solution: For the grade point average (GPA), the confidence interval is
Explanation of Solution
Calculation: The 95% confidence intervals for the grade point average (GPA) is obtained by performing the following steps in Minitab,
Step 1: Enter the data in the worksheet of Minitab.
Step 2: Sort the data for ‘GPA’ on the basis of ‘Gender’. Here, ‘2’ represent the men and ‘1’ represent the women. Go to Data, click on sort, select ‘GPA’ in the ‘Sort column’ and enter ‘Gender’ in the ‘By column’ textbox. Also, store sorted data in the column of current worksheet. After this, make two columns, one for ‘GPA (M)’and other one for ‘GPA (F)’.
Step 3: In a Minitab worksheet go to ‘Stat’ point on ‘Basic Statistics’ and click on ‘2-Sample t’.
Step 4: In the dialogue box that appears select the samples in different column and enter the variable ‘GPA (M)’ in the first textbox and the variable ‘GPA (F)’ in the second textbox.
Step 5: Next click on options tab and set the confidence level as 95 and the Alternative hypothesis as ‘not equal to’. Finally click on OK twice to obtain the output.
Hence, the confidence interval is obtained as
The 95% confidence intervals for the standardized test (IQ) scores is obtained by performing the following steps in Minitab,
Step 1: Enter the data in the worksheet of Minitab.
Step 2: Sort the data for ‘IQ’ on the basis of ‘Gender’. Here, ‘2’ represent the men and ‘1’ represent the women. Go to Data, click on sort, select ‘IQ’ in the ‘Sort column’ and enter ‘Gender’ in the ‘By column’ textbox. Also, store sorted data in the column of current worksheet. After this, make two columns, one for ‘IQ (M)’and other one for ‘IQ (F)’.
Step 3: In a Minitab worksheet go to ‘Stat’ point on ‘Basic Statistics’ and click on ‘2-Sample t’.
Step 4: In the dialogue box that appears select the samples in different column and enter the variable ‘IQ (M)’ in the first textbox and the variable ‘IQ (F)’ in the second textbox.
Step 5: Next click on options tab and set the confidence level as 95 and the Alternative hypothesis as ‘not equal to’. Finally click on OK twice to obtain the output.
Hence, the confidence interval is obtained as
Interpretation: Therefore, it can be concluded that the 95% of the average standardized IQ scores lie between the values
To explain: The findings of the graphical displays, significant test, and confidence intervals for the grade point average (GPA) and a standardized test (IQ) on the basis of gender.
Answer to Problem 143E
Solution: For the grade point average (GPA) and a standardized test (IQ), the results are not significant as the P-value in both the cases are greater than the level of significance 0.05. Also, the distribution appears to be similar in both the cases.
Explanation of Solution
For the grade point average (GPA), the test statistic is
Want to see more full solutions like this?
Chapter 7 Solutions
Introduction to the Practice of Statistics
- Harvard University California Institute of Technology Massachusetts Institute of Technology Stanford University Princeton University University of Cambridge University of Oxford University of California, Berkeley Imperial College London Yale University University of California, Los Angeles University of Chicago Johns Hopkins University Cornell University ETH Zurich University of Michigan University of Toronto Columbia University University of Pennsylvania Carnegie Mellon University University of Hong Kong University College London University of Washington Duke University Northwestern University University of Tokyo Georgia Institute of Technology Pohang University of Science and Technology University of California, Santa Barbara University of British Columbia University of North Carolina at Chapel Hill University of California, San Diego University of Illinois at Urbana-Champaign National University of Singapore McGill…arrow_forwardName Harvard University California Institute of Technology Massachusetts Institute of Technology Stanford University Princeton University University of Cambridge University of Oxford University of California, Berkeley Imperial College London Yale University University of California, Los Angeles University of Chicago Johns Hopkins University Cornell University ETH Zurich University of Michigan University of Toronto Columbia University University of Pennsylvania Carnegie Mellon University University of Hong Kong University College London University of Washington Duke University Northwestern University University of Tokyo Georgia Institute of Technology Pohang University of Science and Technology University of California, Santa Barbara University of British Columbia University of North Carolina at Chapel Hill University of California, San Diego University of Illinois at Urbana-Champaign National University of Singapore…arrow_forwardA company found that the daily sales revenue of its flagship product follows a normal distribution with a mean of $4500 and a standard deviation of $450. The company defines a "high-sales day" that is, any day with sales exceeding $4800. please provide a step by step on how to get the answers in excel Q: What percentage of days can the company expect to have "high-sales days" or sales greater than $4800? Q: What is the sales revenue threshold for the bottom 10% of days? (please note that 10% refers to the probability/area under bell curve towards the lower tail of bell curve) Provide answers in the yellow cellsarrow_forward
- Find the critical value for a left-tailed test using the F distribution with a 0.025, degrees of freedom in the numerator=12, and degrees of freedom in the denominator = 50. A portion of the table of critical values of the F-distribution is provided. Click the icon to view the partial table of critical values of the F-distribution. What is the critical value? (Round to two decimal places as needed.)arrow_forwardA retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. Showing the calculation is a must. If calculation is missing,so please provide a step by step on the answers Numerical answers in the yellow cellsarrow_forwardShow all workarrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





