Chapter 6.6, Problem 68P

6.65 through 6.68 An extruded beam has the cross section shown. Determine (a) the location of the shear center O, (b) the distribution of the shearing stresses caused by the vertical shearing force V shown applied at O.

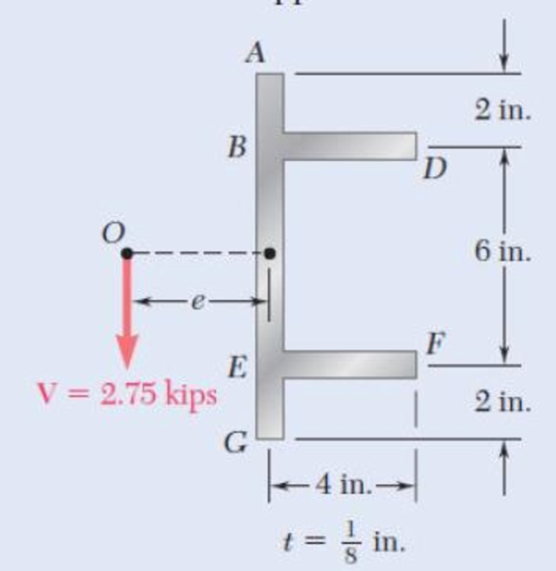
Fig. p6.67

To determine

Find the location of the shear center O.

Answer to Problem 68P

The location of the shear center O is $\underset{\_}{10.22\text{mm}}$.

Explanation of Solution

Calculation:

Calculate the moment of inertia as shown below.

$I=\frac{b{d}^3}{12}+A{\left(y-\overline{y}\right)}^2$

Here, b is the width of the section, d is the height of the section, A is the area of the beam, and $\left(y-\overline{y}\right)$ is the centroid of the beam from the neutral axis.

Calculate the moment of inertia for whole section as shown below.

$\begin{array}{c}I=2\times \left[\frac{1}{12}\times 30\times 6^3+30\times 6\times {45}^2\right]+2\times \left[\frac{1}{12}\times 30\times 4^3+30\times 4\times {15}^2\right]+\frac{1}{12}\times 6\times {90}^3\\ =730,080+54,320+364,500\\ =1.1489\times {10}^6{\text{mm}}^4\end{array}$

Calculate the forces acting along the member as shown below.

$F={\displaystyle \int qdy}$ (1)

Here, $\tau$ is the shear stress.

Sketch the cross section of flange as shown in Figure 1.

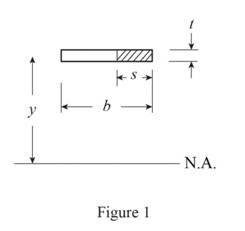
Refer to Figure 1.

Calculate the first moment of area as shown below.

$Q={\displaystyle \sum A\overline{y}}$ (2)

Calculate the first moment of area for AB as shown below.

$Q\left(x\right)=yts$

Calculate the horizontal shear per unit length as shown below.

$q=\frac{VQ}{I}$ (3)

Here, V is the vertical shear.

Substitute $yts$ for Q in Equation (3).

$\begin{array}{c}q=\frac{V\times yts}{I}\\ =\frac{Vyts}{I}\end{array}$

Calculate the force $F_{AB}$ as shown below.

Substitute $\frac{Vyts}{I}$ for q and apply the limits in Equation (1).

$\begin{array}{c}F={\displaystyle \underset{0}{\overset{b}{\int }}\frac{Vyts}{I}ds}\\ =\frac{Vyt}{I}{\left(\frac{s^2}{2}\right)}_0^b\\ =\frac{Vyt{b}^2}{2I}\end{array}$ (4)

For flange AB and flange HJ:

Substitute $45\text{mm}$ for y, $6\text{mm}$ for t, $30\text{mm}$ for b, and $1.1489\times {10}^6{\text{mm}}^4$ for I in Equation (4).

$F_{AB}=F_{HJ}$$\begin{array}{l}=\frac{V\times 45\times 6\times {30}^2}{2\times 1.1489\times {10}^6}\\ =0.10575V\end{array}$

For flange DE and flange FG:

Substitute $15\text{mm}$ for y, $4\text{mm}$ for t, $30\text{mm}$ for b, and $1.1489\times {10}^6{\text{mm}}^4$ for I in Equation (4).

$F_{DE}=F_{FG}$$\begin{array}{l}=\frac{V\times 15\times 4\times {30}^2}{2\times 1.1489\times {10}^6}\\ =0.0235V\end{array}$

Sketch the shear flow as shown in Figure 2.

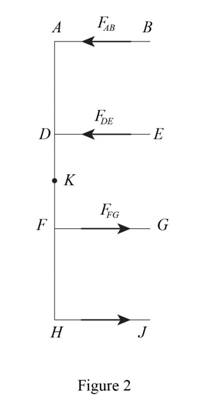
Refer to Figure 2.

Calculate the eccentricity as shown below.

$Ve=45F_{AB}+15F_{DE}+15F_{FG}+45F_{HJ}$

Substitute $0.10575V$ for $F_{AB}$, $0.0235V$ for $F_{DE}$, $0.0235V$ for $F_{FG}$, and $0.10575V$ for $F_{HJ}$.

$\begin{array}{l}Ve=45\times 0.10575V+15\times 0.0235V+15\times 0.0235V+45\times 0.10575V\\ e=10.22\text{mm}\end{array}$

Therefore, the location of the shear center O is $\underset{\_}{10.22\text{mm}}$.

To determine

Find the distribution of the shearing stresses caused by the vertical shearing force.

Answer to Problem 68P

The shearing stress at point B, E, G, and J is $\underset{\_}{0}$.

The shearing stress at point A and H is $\underset{\_}{41.1\text{MPa}}$.

The shearing stress at point just above D and just below F is $\underset{\_}{68.5\text{MPa}}$.

The shearing stress at point just to the right of D and just to the right of F is $\underset{\_}{13.7\text{MPa}}$.

The shearing stress at point just below D and just above F is $\underset{\_}{77.7\text{MPa}}$.

The shearing stress at point K is $\underset{\_}{81.1\text{MPa}}$.

Explanation of Solution

Given information:

The vertical shear is $35\text{kN}$.

Calculation:

Refer to part (a).

The moment of inertia $I=1.1489\times {10}^6{\text{mm}}^4$.

Calculate the shear stress as shown below.

$\tau =\frac{VQ}{It}$ (5)

At point B, E, G, and J:

Calculate the first moment of area as shown below.

$Q=0$

Hence, the shearing stress at point B, E, G, and J is $\underset{\_}{0}$.

At point A and H:

Calculate the first moment of area as shown below.

$\begin{array}{c}Q=30\times 6\times 45\\ =8,100{\text{mm}}^3\end{array}$

The thickness of the section is $6\text{mm}$.

Calculate the shear stress as shown below.

Substitute $35\text{kN}$ for V, $8,100{\text{mm}}^3$ for Q, $6\text{mm}$ for t, and $1.1489\times {10}^6{\text{mm}}^4$ for I in Equation (5).

$\begin{array}{c}\tau =\frac{35\text{kN}\times \frac{1,000\text{N}}{1\text{kN}}\times 8,100{\text{mm}}^3}{1.1489\times {10}^6{\text{mm}}^4\times 6\text{mm}}\\ =\frac{283.5\times {10}^6}{6.8934}\\ =41.1\text{N}/{\text{mm}}^2\times \frac{1\text{MPa}}{1\text{N}/{\text{mm}}^2}\\ =41.1\text{MPa}\end{array}$

Hence, the shearing stress at point A and H is $\underset{\_}{41.1\text{MPa}}$.

At point just above D and just below F:

Calculate the first moment of area as shown below.

$\begin{array}{c}Q=30\times 6\times 45+6\times 30\times 30\\ =8,100+5,400\\ =13,500{\text{mm}}^3\end{array}$

The thickness of the section is $6\text{mm}$.

Calculate the shear stress as shown below.

Substitute $35\text{kN}$ for V, $13,500{\text{mm}}^3$ for Q, $6\text{mm}$ for t, and $1.1489\times {10}^6{\text{mm}}^4$ for I in Equation (5).

$\begin{array}{c}\tau =\frac{35\text{kN}\times \frac{1,000\text{N}}{1\text{kN}}\times 13,500{\text{mm}}^3}{1.1489\times {10}^6{\text{mm}}^4\times 6\text{mm}}\\ =\frac{472.5\times {10}^6}{6.8934}\\ =68.5\text{N}/{\text{mm}}^2\times \frac{1\text{MPa}}{1\text{N}/{\text{mm}}^2}\\ =68.5\text{MPa}\end{array}$

Hence, the shearing stress at point just above D and just below F is $\underset{\_}{68.5\text{MPa}}$.

At point just to the right of D and just to the right of F:

Calculate the first moment of area as shown below.

$\begin{array}{c}Q=30\times 4\times 15\\ =1,800{\text{mm}}^3\end{array}$

The thickness of the section is $4\text{mm}$.

Calculate the shear stress as shown below.

Substitute $35\text{kN}$ for V, $1,800{\text{mm}}^3$ for Q, $4\text{mm}$ for t, and $1.1489\times {10}^6{\text{mm}}^4$ for I in Equation (5).

$\begin{array}{c}\tau =\frac{35\text{kN}\times \frac{1,000\text{N}}{1\text{kN}}\times 1,800{\text{mm}}^3}{1.1489\times {10}^6{\text{mm}}^4\times 4\text{mm}}\\ =\frac{63\times {10}^6}{4.5956}\\ =13.7\text{N}/{\text{mm}}^2\times \frac{1\text{MPa}}{1\text{N}/{\text{mm}}^2}\\ =13.7\text{MPa}\end{array}$

Hence, the shearing stress at point just to the right of D and just to the right of F is $\underset{\_}{13.7\text{MPa}}$.

At point just below D and just above F:

Calculate the first moment of area as shown below.

$\begin{array}{c}Q=30\times 6\times 45+6\times 30\times 30+30\times 4\times 15\\ =8,100+5,400+1,800\\ =15,300{\text{mm}}^3\end{array}$

The thickness of the section is $6\text{mm}$.

Calculate the shear stress as shown below.

Substitute $35\text{kN}$ for V, $15,300{\text{mm}}^3$ for Q, $6\text{mm}$ for t, and $1.1489\times {10}^6{\text{mm}}^4$ for I in Equation (5).

$\begin{array}{c}\tau =\frac{35\text{kN}\times \frac{1,000\text{N}}{1\text{kN}}\times 15,300{\text{mm}}^3}{1.1489\times {10}^6{\text{mm}}^4\times 6\text{mm}}\\ =\frac{535.5\times {10}^6}{6.8934}\\ =77.7\text{N}/{\text{mm}}^2\times \frac{1\text{MPa}}{1\text{N}/{\text{mm}}^2}\\ =77.7\text{MPa}\end{array}$

Hence, the shearing stress at point just below D and just above F is $\underset{\_}{77.7\text{MPa}}$.

At point just below D and just above F:

Calculate the first moment of area as shown below.

$\begin{array}{c}Q=30\times 6\times 45+6\times 30\times 30+30\times 4\times 15\\ =8,100+5,400+1,800\\ =15,300{\text{mm}}^3\end{array}$

The thickness of the section is $6\text{mm}$.

Calculate the shear stress as shown below.

Substitute $35\text{kN}$ for V, $15,300{\text{mm}}^3$ for Q, $6\text{mm}$ for t, and $1.1489\times {10}^6{\text{mm}}^4$ for I in Equation (5).

$\begin{array}{c}\tau =\frac{35\text{kN}\times \frac{1,000\text{N}}{1\text{kN}}\times 15,300{\text{mm}}^3}{1.1489\times {10}^6{\text{mm}}^4\times 6\text{mm}}\\ =\frac{535.5\times {10}^6}{6.8934}\\ =77.7\text{N}/{\text{mm}}^2\times \frac{1\text{MPa}}{1\text{N}/{\text{mm}}^2}\\ =77.7\text{MPa}\end{array}$

Hence, the shearing stress at point just below D and just above F is $\underset{\_}{77.7\text{MPa}}$.

At point K:

Calculate the first moment of area as shown below.

$\begin{array}{c}Q=30\times 6\times 45+6\times 30\times 30+30\times 4\times 15+6\times 15\times 7.5\\ =8,100+5,400+1,800+675\\ =15,975{\text{mm}}^3\end{array}$

The thickness of the section is $6\text{mm}$.

Calculate the shear stress as shown below.

Substitute $35\text{kN}$ for V, $15,975{\text{mm}}^3$ for Q, $6\text{mm}$ for t, and $1.1489\times {10}^6{\text{mm}}^4$ for I in Equation (5).

$\begin{array}{c}\tau =\frac{35\text{kN}\times \frac{1,000\text{N}}{1\text{kN}}\times 15,975{\text{mm}}^3}{1.1489\times {10}^6{\text{mm}}^4\times 6\text{mm}}\\ =\frac{559.125\times {10}^6}{6.8934}\\ =81.1\text{N}/{\text{mm}}^2\times \frac{1\text{MPa}}{1\text{N}/{\text{mm}}^2}\\ =81.1\text{MPa}\end{array}$

Therefore, the shearing stress at point K is $\underset{\_}{81.1\text{MPa}}$.