Chapter 6.5, Problem 37E

(a)

To determine

The value of $f\text{'}$

Answer to Problem 37E

The value is $f\text{'}\text{'}\left(x\right)=2\cos \left(x^2\right)-4x^2\sin \left(x^2\right)$

Explanation of Solution

Given information:

Consider the ${\displaystyle \underset{-1}{\overset{1}{\int }}\sin \left(x^2\right)dx}$

Formula used:

  $f\text{'}\left(x\right)=\frac{d}{dx}\left(\sin \left(x^2\right)\right)$

Calculation:

Take derivative both sides

  $\begin{array}{l}f\text{'}\left(x\right)=\frac{d}{dx}\left(\sin \left(x^2\right)\right)\\ =\frac{d\left(\sin \left(x^2\right)\right)}{d\left(x^2\right)}\frac{d\left(x^2\right)}{dx}\\ f\text{'}\left(x\right)=\cos \left(x^2\right)\left[2x\right]\end{array}$

Now, again take derivative

  $\begin{array}{l}f\text{'}\text{'}\left(x\right)=\frac{d}{dx}\left[2x\cos \left(x^2\right)\right]\\ =2x\frac{d\left[\cos \left(x^2\right)\right]}{d\left(x^2\right)}\frac{d\left(x^2\right)}{dx}+\cos \left(x^2\right)\frac{d\left(2x\right)}{dx}\\ =-2x\sin \left(x^2\right)\left[2x\right]+2\cos \left(x^2\right)\\ f\text{'}\text{'}\left(x\right)=2\cos \left(x^2\right)-4x^2\sin \left(x^2\right)\end{array}$

Conclusion:

The value is $f\text{'}\text{'}\left(x\right)=2\cos \left(x^2\right)-4x^2\sin \left(x^2\right)$

(b)

To determine

To sketch: The graph of the function $y=f\text{'}(x)$

Answer to Problem 37E

The value gets decreases on the negative values.

Explanation of Solution

Given information:

Consider the ${\displaystyle \underset{-1}{\overset{1}{\int }}\sin \left(x^2\right)dx}$

Formula used:

The graph is plotted against the x and y axis.

Calculation:

The graph of $y=f"\left(x\right)$ within the given interval is

  

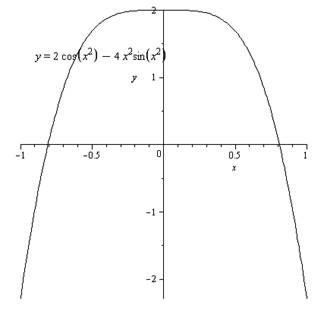
Conclusion:

The value gets decreases on the negative values.

(c)

To determine

The value of $|f\text{'}(x)|$

Answer to Problem 37E

The modulus of $f"\left(x\right)$ is less than or equal to 3

Explanation of Solution

Given information:

Consider the ${\displaystyle \underset{-1}{\overset{1}{\int }}\sin \left(x^2\right)dx}$

Formula used:

  $-1\le x\le 1$

Calculation:

Observe the graph,

For $-1\le x\le 1$

  $-3\le f"\left(x\right)\le 2$

Hence modulus of $f"\left(x\right)$ is less than or equal to 3.

Conclusion:

The modulus of $f"\left(x\right)$ is less than or equal to 3

(d)

To determine

The error estimate of the trapezoidal rule.

Answer to Problem 37E

The value is $\left|E_r\right|\le \frac{h^2}{2}$

Explanation of Solution

Given information:

Consider the ${\displaystyle \underset{-1}{\overset{1}{\int }}\sin \left(x^2\right)dx}$

Formula used:

  $\left|E_r\right|\le \frac{b-a}{12}{h}^2{M}_{\stackrel{·}{f}}$

Calculation:

If T represents the approximation to ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)}dx$ given by the trapezoidal rule, then the errors E_Tsatisfy

  $\left|E_r\right|\le \frac{b-a}{12}{h}^2{M}_{\stackrel{·}{f}}$

  $M_{\stackrel{·}{f}}$ it is maximum value of $\left|\stackrel{·}{f}\right|$ on $\left[a,b\right]$

Since,

  $\begin{array}{l}\left[a,b\right]=\left[-1,1\right]\\ \left|f"\right|=3\end{array}$

Hence,

  $\begin{array}{l}\left|E_r\right|\le \frac{1-\left(-1\right)}{12}{h}^3\left(3\right)\\ \le \frac{6}{12}{h}^2\\ \left|E_r\right|\le \frac{h^2}{2}\end{array}$

Conclusion:

The value is $\left|E_r\right|\le \frac{h^2}{2}$

(e)

To determine

The trapezoidal rule error having the values less than or equal to 0.01.

Answer to Problem 37E

The value is less than 0.01.

Explanation of Solution

Given information:

Consider the ${\displaystyle \underset{-1}{\overset{1}{\int }}\sin \left(x^2\right)dx}$

Formula used:

  $\left|E_r\right|\le \frac{h^2}{2}$

Calculation:

If $h\le 0.1$

  $\begin{array}{l}\left|E_r\right|\le \frac{h^2}{2}\\ \le \frac{{\left(0.1\right)}^2}{2}\\ \left|E_r\right|\le 0.005\end{array}$

This is less than 0.01.

Conclusion:

The value is less than 0.01.

(f)

To determine

The larger value of n.

Answer to Problem 37E

The value will be $n\ge 20$

Explanation of Solution

Given information:

Consider the ${\displaystyle \underset{-1}{\overset{1}{\int }}\sin \left(x^2\right)dx}$

Formula used:

  $n=\frac{b-a}{h}$

Calculation:

Since,

  $n=\frac{b-a}{h}$

So,

  $\begin{array}{l}h=\frac{b-a}{n}\\ \frac{b-a}{n}\le 0.1\\ n\ge \frac{1-\left(-1\right)}{0.1}\end{array}$

Therefore,

  $n\ge 20$

Conclusion:

The value will be $n\ge 20$