
Concept explainers
(a)
H(0) with f being a continuous function.
(a)
Answer to Problem 57E
With f being a continuous function,
13y
Explanation of Solution
Given information:
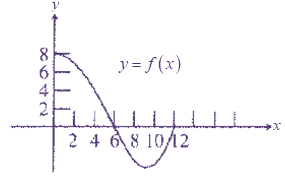
Where,
f is a continuous function with domain [0,12].
We have
Substitute
Thus,
No area under the curve exists on the interval [0, 0], because this area will have no width.
(b)
Interval on which H is increasing.
(b)
Answer to Problem 57E
H(x) is increasing on [0, 6].
Explanation of Solution
Given information:
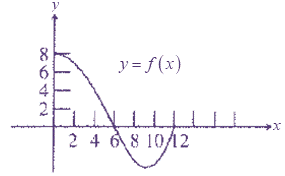
Where,
f is a continuous function with domain [0,12].
H is increasing on interval [a, b],
When
For
(a,b).
Since
And
For all
Thus,
H(x) is increasing on [0, 6].
(c)
Interval on which the graph of H concave up.
(c)
Answer to Problem 57E
H is concave up on the interval [9, 12].
Explanation of Solution
Given information:
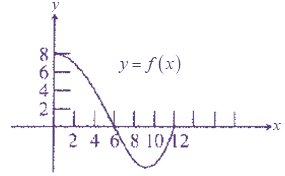
Where,
f is a continuous function with domain [0,12].
For H to be concave up,
The second derivative needs to be positive.
Since
As well as
Thus,
In other words,
H is concave up when slope of the graph
According to graph,
This occurs when x is between 9 and 12.
Therefore,
H is concave up on the interval [9, 12].
(d)
Whether H(12) is positive or negative.
(d)
Answer to Problem 57E
H(12) is positive.
Explanation of Solution
Given information:
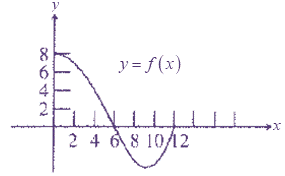
Where,
f is a continuous function with domain [0,12].
The region between curve and x-axis,
Since the net area of the region above the x-axis between 0 and 6 is larger than the net area of the region below the x-axis between 6 and 12,
The total region between the curve and x-axis will be positive.
Thus,
H(12) is positive.
(e)
Point at which H achieves maximum value.
(e)
Answer to Problem 57E
H achieves maximum value at
Explanation of Solution
Given information:
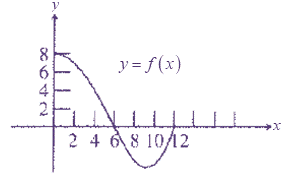
Where,
f is a continuous function with domain [0,12].
H(x) will achieve its maximum at an endpoint or a value of x.
Such that
Since
And
When
Then
Since
And
Then
Therefore,
H achieves its maximum value at
(f)
Point at which H achieves minimum value.
(f)
Answer to Problem 57E
H achieves minimum value at
Explanation of Solution
Given information:
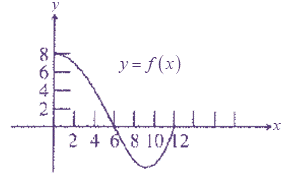
Where,
f is a continuous function with domain [0,12].
H will achieve its minimum value at an endpoint or critical point.
From Part (e),
The only critical point was at
Then
H will achieve its minimum at one of its endpoints at
From Part (b),
Since
For all x between
H is always increasing.
That means
Therefore,
H achieves minimum value at
Chapter 6 Solutions
Calculus: Graphical, Numerical, Algebraic
Additional Math Textbook Solutions
Elementary Statistics (13th Edition)
Pre-Algebra Student Edition
A First Course in Probability (10th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Calculus: Early Transcendentals (2nd Edition)
- Solve this question and show steps.arrow_forwardu, v and w are three coplanar vectors: ⚫ w has a magnitude of 10 and points along the positive x-axis ⚫ v has a magnitude of 3 and makes an angle of 58 degrees to the positive x- axis ⚫ u has a magnitude of 5 and makes an angle of 119 degrees to the positive x- axis ⚫ vector v is located in between u and w a) Draw a diagram of the three vectors placed tail-to-tail at the origin of an x-y plane. b) If possible, find w × (ū+v) Support your answer mathematically or a with a written explanation. c) If possible, find v. (ū⋅w) Support your answer mathematically or a with a written explanation. d) If possible, find u. (vxw) Support your answer mathematically or a with a written explanation. Note: in this question you can work with the vectors in geometric form or convert them to algebraic vectors.arrow_forwardQuestion 3 (6 points) u, v and w are three coplanar vectors: ⚫ w has a magnitude of 10 and points along the positive x-axis ⚫ v has a magnitude of 3 and makes an angle of 58 degrees to the positive x- axis ⚫ u has a magnitude of 5 and makes an angle of 119 degrees to the positive x- axis ⚫ vector v is located in between u and w a) Draw a diagram of the three vectors placed tail-to-tail at the origin of an x-y plane. b) If possible, find w × (u + v) Support your answer mathematically or a with a written explanation. c) If possible, find v. (ū⋅ w) Support your answer mathematically or a with a written explanation. d) If possible, find u (v × w) Support your answer mathematically or a with a written explanation. Note: in this question you can work with the vectors in geometric form or convert them to algebraic vectors.arrow_forward
- K Find all values x = a where the function is discontinuous. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist. x-7 p(x) = X-7 Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. (Use a comma to separate answers as needed.) OA. f is discontinuous at the single value x = OB. f is discontinuous at the single value x= OC. f is discontinuous at the two values x = OD. f is discontinuous at the two values x = The limit is The limit does not exist and is not co or - ∞. The limit for the smaller value is The limit for the larger value is The limit for the smaller value is The limit for the larger value does not exist and is not c∞ or -arrow_forwardK x3 +216 complete the table and use the results to find lim k(x). If k(x) = X+6 X-6 X -6.1 -6.01 - 6.001 - 5.999 - 5.99 -5.9 k(x) Complete the table. X -6.1 -6.01 - 6.001 - 5.999 - 5.99 - 5.9 k(x) (Round to three decimal places as needed.) Find the limit. Select the correct choice below and, if necessary, fill in the answer box within your choice.arrow_forwardSketch the slope field that represents the differential equation. × Clear Undo Redo y ४|० || 33 dy dxarrow_forward
- Sketch the slope field that represents the differential equation. × Clear Undo Redo dy 33 dx = -y "arrow_forwardMath Test 3 3 x³+y³ = Ꭹ = 9 2 2 x²+y² = 5 x+y=?arrow_forwardFor each of the following series, determine whether the absolute convergence series test determines absolute convergence or fails. For the ¿th series, if the test is inconclusive then let Mi = 4, while if the test determines absolute convergence let Mi 1 : 2: ∞ Σ(−1)"+¹ sin(2n); n=1 Σ n=1 Σ ((−1)”. COS n² 3+2n4 3: (+ 4: 5 : n=1 ∞ n 2+5n3 ПП n² 2 5+2n3 пп n² Σ(+)+ n=1 ∞ n=1 COS 4 2 3+8n3 П ηπ n- (−1)+1 sin (+727) 5 + 2m³ 4 = 8. Then the value of cos(M₁) + cos(2M2) + cos(3M3) + sin(2M) + sin(M5) is -0.027 -0.621 -1.794 -1.132 -1.498 -4.355 -2.000 2.716arrow_forward
- i need help with this question i tried by myself and so i am uploadding the question to be quided with step by step solution and please do not use chat gpt i am trying to learn thank you.arrow_forwardi need help with this question i tried by myself and so i am uploadding the question to be quided with step by step solution and please do not use chat gpt i am trying to learn thank you.arrow_forward1. 3 2 fx=14x²-15x²-9x- 2arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





