Chapter 6.3, Problem 69E

Beehives In a beehive each cell is a regular hexagonal prism, as shown in the figure. The amount of wax W in the cell depends on the apex angle θ and is given by

$W=3.02-0.38\cot \theta +0.65\csc \theta$

Bees instinctively choose θ so as to use the least amount of wax possible.

1. (a) Use a graphing device to graph W as a function of θ for 0 < θ < π.
2. (b) For what value of θ does W have its minimum value? [Note: Biologists have discovered that bees rarely deviate from this value by more than a degree or two.]

To determine

To sketch: The graph of $W=3.02-0.38\cot \theta +0.65\csc \theta$ as a function of $\theta$ for $0<\theta <\pi$.

Explanation of Solution

The given function is,

$W=3.02-0.38\cot \theta +0.65\csc \theta$ (1)

The amount of wax in each cell is represented by W and $\theta$ is the angle formed by the sides of the trihedron and the vertical axis of the cell.

Sketch the graph of W with respect to $\theta$.

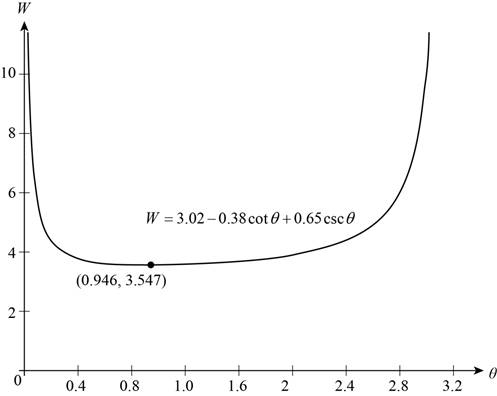
Figure (1)

Figure (1) shows the graph of $W=3.02-0.38\cot \theta +0.65\csc \theta$ where $\theta$ is in radian.

To determine

To find: The value of $\theta$ for which the function $W=3.02-0.38\cot \theta +0.65\csc \theta$ has minimum value.

Answer to Problem 69E

The amount of wax W is minimum for $\theta =0.95\text{rad}$ or $\theta =54°$.

Explanation of Solution

In beehive, each cell is regular hexagonal prism, open at one end with a trihedron at the other end.

The amount of wax in each cell is represented by W and $\theta$ is the angle formed by the sides of the trihedron and the vertical axis of the cell.

The given relation between W and $\theta$ is,

$W=3.02-0.38\cot \theta +0.65\csc \theta$

From close examination of part (a) it is clear that the lowest part of the curve is at $\theta =0.95\text{rad}$ or $\theta =54°$

Thus, for $\theta =0.95\text{rad}$ or $\theta =54°$ the amount of wax W is minimum.