Chapter 6.2, Problem 16E

To determine

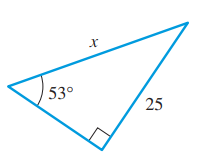
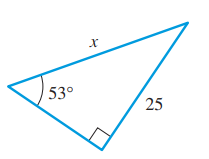
To calculate: The value of length of side x of the right angled triangle.

Answer to Problem 16E

The value of length of side x of the right angled triangle is $31.30339$ units.

Explanation of Solution

Given information:

The right angle triangle with length of its sides and angle.

Formula used:

The trigonometric ratios for a right angle triangle are defined as,

  $\sin \theta =\frac{\text{opposite}}{\text{hypotenuse}},cos\theta =\frac{\text{adjacent}}{\text{hypotenuse}},\tan \theta =\frac{\text{opposite}}{\text{adjacent}},\csc \theta =\frac{\text{hypotenuse}}{\text{opposite}},\sec \theta =\frac{\text{hypotenuse}}{\text{adjacent}}$ and $\cot \theta =\frac{\text{adjacent}}{\text{opposite}}$ .

Calculation:

Consider the right angle triangle with length of its sides and angle.

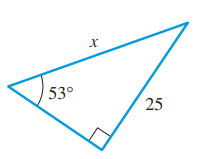
Observe that opposite side is of length 25units and hypotenuse has length x units.

Recall that the sine trigonometric ratio for a right angle triangle is defined as, $\sin \theta =\frac{\text{opposite}}{\text{hypotenuse}}$ .

Apply it, to estimate the value of trigonometric ratios,

The value of sine function is,

  $\begin{array}{c}\sin 53°=\frac{\text{opposite}}{\text{hypotenuse}}\\ \sin 53°=\frac{25}{x}\end{array}$

Multiply each side by x ,

  $\begin{array}{c}\sin 53°\cdot x=\frac{25}{x}\cdot x\\ x\sin 53°=25\end{array}$

Divide each side by $\sin 53°$ ,

  $\begin{array}{c}\sin 53°\cdot x=\frac{25}{x}\cdot x\\ \frac{x\sin 53°}{\sin 53°}=\frac{25}{\sin 53°}\\ x=\frac{25}{\sin 53°}\end{array}$

Simplify with help of calculator,

  $x=31.30339$

Thus, the value of length of side x of the right angled triangle is $31.30339$ units.