Chapter 6.2, Problem 10E

$\left(a\right)$

To determine

To calculate: The value of trigonometric ratios $\sin \alpha \text{ and }\cos \beta$ provided in the triangle.

Answer to Problem 10E

The value of trigonometric ratiosare $\sin \alpha =\frac{4}{7}\text{ and }\cos \beta =\frac{4}{7}$ .

Explanation of Solution

Given information:

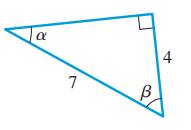
The right angle triangle with length of its sides and angles $\alpha \text{ and }\beta$ .

Formula used:

The trigonometric ratios for a right angle triangle are defined as,

  $\sin \theta =\frac{\text{opposite}}{\text{hypotenuse}}\text{ and }cos\theta =\frac{\text{adjacent}}{\text{hypotenuse}}$ .

Calculation:

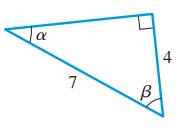
The right angle triangle with length of its sides and angles $\alpha \text{ and }\beta$ .

First consider the opposite, adjacent and hypotenuse with respect to angle $\alpha$ .

Observe that opposite side is of length 4 units and hypotenuse has length 7 units.

Now, let the length of adjacent side be x , as it is a right angle triangle so,

  $\begin{array}{c}{4}^2+x^2=7^2\\ x^2=49-16\\ x^2=33\\ x=\sqrt{33}\end{array}$

Therefore, length of adjacent side is $\sqrt{33}$ units.

Recall that the sine trigonometric ratio for a right angle triangle is defined as, $\sin \theta =\frac{\text{opposite}}{\text{hypotenuse}}$ .

Apply it, to estimate the value of trigonometric ratios,

The value of sine function is,

  $\begin{array}{c}\sin \alpha =\frac{\text{opposite}}{\text{hypotenuse}}\\ =\frac{4}{7}\end{array}$

Second consider the opposite, adjacent and hypotenuse with respect to angle $\beta$ .

Observe that adjacent side is of length 4 units and hypotenuse has length 7 units.

Now, let the length of opposite side be x , as it is a right angle triangle so,

  $\begin{array}{c}{4}^2+x^2=7^2\\ x^2=49-16\\ x^2=33\\ x=\sqrt{33}\end{array}$

Therefore, length of opposite side is $\sqrt{33}$ units.

Recall that the cosine trigonometric ratio for a right angle triangle is defined as, $cos\theta =\frac{\text{adjacent}}{\text{hypotenuse}}$ .

Apply it, to estimate the value of trigonometric ratios,

The value of cosine function is,

  $\begin{array}{c}\cos \beta =\frac{\text{adjacent}}{\text{hypotenuse}}\\ =\frac{4}{7}\end{array}$

Thus, the value of trigonometric ratiosare $\sin \alpha =\frac{4}{7}\text{ and }\cos \beta =\frac{4}{7}$ .

  $\left(b\right)$

To determine

To calculate: The value of trigonometric ratios $\tan \alpha \text{ and }\cot \beta$ provided in the triangle.

Answer to Problem 10E

The value of trigonometric ratiosare $\tan \alpha =\frac{4\sqrt{33}}{33}\text{ and }\cot \beta =\frac{4\sqrt{33}}{33}$ .

Explanation of Solution

Given information:

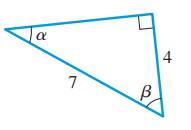
The right angle triangle with length of its sides and angles $\alpha \text{ and }\beta$ .

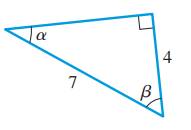
Formula used:

The trigonometric ratios for a right angle triangle are defined as,

  $\tan \theta =\frac{\text{opposite}}{\text{adjacent}}\text{ and }\cot \theta =\frac{\text{adjacent}}{\text{opposite}}$ .

Calculation:

The right angle triangle with length of its sides and angles $\alpha \text{ and }\beta$ .

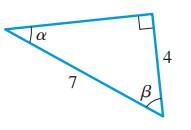
First consider the opposite, adjacent and hypotenuse with respect to angle $\alpha$ .

Observe that opposite side is of length 4 units and hypotenuse has length 7 units.

Now, let the length of adjacent side be x , as it is a right angle triangle so,

  $\begin{array}{c}{4}^2+x^2=7^2\\ x^2=49-16\\ x^2=33\\ x=\sqrt{33}\end{array}$

Therefore, length of adjacent side is $\sqrt{33}$ units.

Recall that the tangent trigonometric ratio for a right angle triangle is defined as, $\tan \theta =\frac{\text{opposite}}{\text{adjacent}}$ .

Apply it, to estimate the value of trigonometric ratios,

The value of tangent function is,

  $\begin{array}{c}\tan \alpha =\frac{\text{opposite}}{\text{adjacent}}\\ =\frac{4}{\sqrt{33}}\\ =\frac{4\sqrt{33}}{33}\end{array}$

Second consider the opposite, adjacent and hypotenuse with respect to angle $\beta$ .

Observe that adjacent side is of length 4 units and hypotenuse has length 7 units.

Now, let the length of opposite side be x , as it is a right angle triangle so,

  $\begin{array}{c}{4}^2+x^2=7^2\\ x^2=49-16\\ x^2=33\\ x=\sqrt{33}\end{array}$

Therefore, length of opposite side is $\sqrt{33}$ units.

Recall that the cosine trigonometric ratios for a right angle triangle is defined as, $\cot \theta =\frac{\text{adjacent}}{\text{opposite}}$ .

Apply it, to estimate the value of trigonometric ratios,

The value of cotangent function is,

  $\begin{array}{c}\cot \beta =\frac{\text{adjacent}}{\text{opposite}}\\ =\frac{4}{\sqrt{33}}\\ =\frac{4\sqrt{33}}{33}\end{array}$

Thus, the value of trigonometric ratiosare $\tan \alpha =\frac{4\sqrt{33}}{33}\text{ and }\cot \beta =\frac{4\sqrt{33}}{33}$ .

  $\left(c\right)$

To determine

To calculate: The value of trigonometric ratios $\sec \alpha \text{ and }\csc \beta$ provided in the triangle.

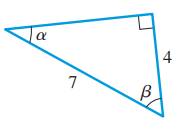
Answer to Problem 10E

The value of trigonometric ratiosare $\sec \alpha =\frac{7\sqrt{33}}{33}\text{ and }\csc \beta =\frac{7\sqrt{33}}{33}$ .

Explanation of Solution

Given information:

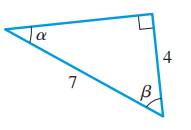
The right angle triangle with length of its sides and angles $\alpha \text{ and }\beta$ .

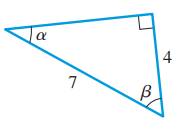
Formula used:

The trigonometric ratios for a right angle triangle are defined as,

  $\csc \theta =\frac{\text{hypotenuse}}{\text{opposite}}\text{ and }\sec \theta =\frac{\text{hypotenuse}}{\text{adjacent}}$ .

Calculation:

The right angle triangle with length of its sides and angles $\alpha \text{ and }\beta$ .

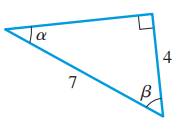
First consider the opposite, adjacent and hypotenuse with respect to angle $\alpha$ .

Observe that opposite side is of length 4 units and hypotenuse has length 7 units.

Now, let the length of adjacent side be x , as it is a right angle triangle so,

  $\begin{array}{c}{4}^2+x^2=7^2\\ x^2=49-16\\ x^2=33\\ x=\sqrt{33}\end{array}$

Therefore, length of adjacent side is $\sqrt{33}$ units.

Recall that the secant trigonometric ratio for a right angle triangle is defined as, $sec\theta =\frac{\text{hypotenuse}}{\text{adjacent}}$ .

Apply it, to estimate the value of trigonometric ratios,

The value of secant function is,

  $\begin{array}{c}\sec \alpha =\frac{\text{hypotenuse}}{\text{adjacent}}\\ =\frac{7}{\sqrt{33}}\\ =\frac{7\sqrt{33}}{33}\end{array}$

Second consider the opposite, adjacent and hypotenuse with respect to angle $\beta$ .

Observe that adjacent side is of length 4 units and hypotenuse has length 7 units.

Now, let the length of opposite side be x , as it is a right angle triangle so,

  $\begin{array}{c}{4}^2+x^2=7^2\\ x^2=49-16\\ x^2=33\\ x=\sqrt{33}\end{array}$

Therefore, length of opposite side is $\sqrt{33}$ units.

Recall that the cosecant trigonometric ratios for a right angle triangle is defined as, $\csc \theta =\frac{\text{hypotenuse}}{\text{opposite}}$ .

Apply it, to estimate the value of trigonometric ratios,

The value of cosecant function is,

  $\begin{array}{c}\csc \beta =\frac{\text{hypotenuse}}{\text{opposite}}\\ =\frac{7}{\sqrt{33}}\\ =\frac{7\sqrt{33}}{33}\end{array}$

Thus, the value of trigonometric ratiosare $\sec \alpha =\frac{7\sqrt{33}}{33}\text{ and }\csc \beta =\frac{7\sqrt{33}}{33}$ .