Linear Algebra with Applications (9th Edition) (Featured Titles for Linear Algebra (Introductory))
9th Edition
ISBN: 9780321962218
Author: Steven J. Leon
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6.3, Problem 26E
Consider a Web network consisting of only four sites that are linked together as shown in the ac-
companying diagram. If the Google PageRank algorithm is used to rank these pages, determine the transition matrix A. Assume that the Web surfer will follow a link on the current page 85 percent of the time.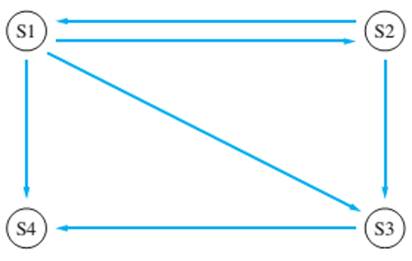 
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Co Given
show that
Solution
Take home
Су-15
1994
+19
09/2
4
=a
log
суто
-
1092
ж
= a-1
2+1+8
AI | SHOT ON S4
INFINIX CAMERA
a
Question 7. If det d e f
ghi
V3
= 2. Find det
-1
2
Question 8. Let A = 1
4
5
0
3
2.
1 Find adj (A)
2 Find det (A)
3
Find A-1
2g 2h 2i
-e-f
-d
273
2a 2b 2c
Question 1. Solve the system
-
x1 x2 + 3x3 + 2x4
-x1 + x22x3 + x4
2x12x2+7x3+7x4
Question 2. Consider the system
= 1
=-2
= 1
3x1 - x2 + ax3
= 1
x1 + 3x2 + 2x3
x12x2+2x3
= -b
= 4
1 For what values of a, b will the system be inconsistent?
2 For what values of a, b will the system have only one solution?
For what values of a, b will the saystem have infinitely many solutions?
Chapter 6 Solutions
Linear Algebra with Applications (9th Edition) (Featured Titles for Linear Algebra (Introductory))
Ch. 6.1 - Find the eigenvalues and the corresponding...Ch. 6.1 - Show that the eigenvalues of a triangular matrix...Ch. 6.1 - Let A be an nn matrix. Prove that A is singular if...Ch. 6.1 - Let A be a nonsingular matrix and let be an...Ch. 6.1 - Let A and B be nn matrices. Show that if none of...Ch. 6.1 - Let be an eigenvalue of A and let x be an...Ch. 6.1 - Let A bean nn matrix and let B=I2A+A2. Show that...Ch. 6.1 - An nn matrix A is said to be idempotent if A2=A....Ch. 6.1 - An nn matrix is said to be nilpotent if Ak=O for...Ch. 6.1 - Let A be an nn matrix and let B=AI for some scalar...
Ch. 6.1 - Let A be an nn matrix and let B=A+I. Is it...Ch. 6.1 - Show that A and AT have the same eigenvalues. Do...Ch. 6.1 - Show that the matrix A=( cos sin sin cos) will...Ch. 6.1 - Let A be a 22 matrix. If tr(A)=8 and det(A)=12,...Ch. 6.1 - Let A=(aij) be an nn matrix with eigenvalues...Ch. 6.1 - Prob. 16ECh. 6.1 - Prob. 17ECh. 6.1 - Let A be an nn matrix and let be an eigenvalue of...Ch. 6.1 - Prob. 19ECh. 6.1 - Let =+bi and =c+di be complex scalars and let A...Ch. 6.1 - Let Q be an orthogonal matrix. Show that if is an...Ch. 6.1 - Let Q be an orthogonal matrix with an eigenvalue...Ch. 6.1 - Let Q be a 33 orthogonal matrix whose determinant...Ch. 6.1 - Let x1,...,xr be eigenvectors of an nn matrix A...Ch. 6.1 - Let A bean nn matrix and let be an eigenvalue of...Ch. 6.1 - Let B=S1AS and let x be an eigenvector of B...Ch. 6.1 - Let A be an nn matrix with an eigenvalue and let...Ch. 6.1 - Prob. 28ECh. 6.1 - Let A be an nn matrix and let be a nonzero...Ch. 6.1 - Prob. 30ECh. 6.1 - Let A be a matrix whose columns all add up to a...Ch. 6.1 - Let 1 and 2 be distinct eigenvalues of A. Let x be...Ch. 6.1 - Let A and B be nn matrices. Show that (a) If is a...Ch. 6.1 - Prove that there do not exist nn matrices A and B...Ch. 6.1 - Let p()=(1)n(nan1n1a1a0) be a polynomial of degree...Ch. 6.1 - The result given in Exercise 35(b) holds even if...Ch. 6.2 - Find the general solution of each of the following...Ch. 6.2 - Solve each of the following initial value...Ch. 6.2 - Given Y=c1e1tx1+c2e2tx2++cnentxn is the solution...Ch. 6.2 - Two tanks each contain 100 liters of a mixture....Ch. 6.2 - Prob. 5ECh. 6.2 - Solve the initial value problem...Ch. 6.2 - In Application 2, assume that the solutions are of...Ch. 6.2 - Solve the the problem in Application 2, using the...Ch. 6.2 - Prob. 9ECh. 6.2 - Three masses are connected by a series of springs...Ch. 6.2 - Transform the nth-order equation...Ch. 6.3 - In each of the following, factor the matrix A into...Ch. 6.3 - For each of the matrices in Exercise 1, use the...Ch. 6.3 - For each of the nonsingular matrices in Exercise...Ch. 6.3 - For each of the following, find a matrix B such...Ch. 6.3 - Let A be a nondefective nn matrix with...Ch. 6.3 - Let A be a diagonalizable matrix whose eigenvalues...Ch. 6.3 - Show that any 33 matrix of the form (a100a100b) is...Ch. 6.3 - For each of the following, find all possible...Ch. 6.3 - Let A be a 44 matrix and let be an eigenvalue of...Ch. 6.3 - Prob. 10ECh. 6.3 - Let A be a nn matrix with real entries and let...Ch. 6.3 - Let A be an nn matrix with an eigenvalue of...Ch. 6.3 - Show that a nonzero nilpotent matrix is defective.Ch. 6.3 - Let A be a diagonalizable matrix and let X be the...Ch. 6.3 - It follows from Exercise 14 that for a...Ch. 6.3 - Prob. 16ECh. 6.3 - Let x, y, be nonzero vectors in n,n2, and let...Ch. 6.3 - Let A be a diagonalizable nn matrix. Prove that if...Ch. 6.3 - Prob. 19ECh. 6.3 - Let T be an upper triangular matrix with distinct...Ch. 6.3 - Each year, employees at a company are given the...Ch. 6.3 - The city of Mawtookit maintains a constant...Ch. 6.3 - Let A=( 1 2 1 3 1 5 1 4 1 3 2 5 1 4 1 3 2 5 ) be a...Ch. 6.3 - Prob. 24ECh. 6.3 - Prob. 25ECh. 6.3 - Consider a Web network consisting of only four...Ch. 6.3 - Prob. 27ECh. 6.3 - The transition matrix in Example 5 has the...Ch. 6.3 - Let A be the PageRank transition matrix and let xk...Ch. 6.3 - Use the definition of the matrix exponential to...Ch. 6.3 - Compute eA for each of the following matrices: A=(...Ch. 6.3 - In each of the following, solve the initial value...Ch. 6.3 - Let X be an eigenvalue of an nn matrix A and let x...Ch. 6.3 - Show that eA is nonsingular for any diagonalizable...Ch. 6.3 - Let A be a diagonalizable matrix with...Ch. 6.4 - For each of the following pairs of vectors z and...Ch. 6.4 - Let z1=( 1+i 2 1i 2 ) and z2=( i 2 1 2 ) Show...Ch. 6.4 - Let {u1,u2} be an orthonormal basis for 2, and let...Ch. 6.4 - Which of the matrices that follow are Hermitian?...Ch. 6.4 - Find an orthogonal or unitary diagonalizing matrix...Ch. 6.4 - Prob. 6ECh. 6.4 - Let A be an nn Hermitian matrix and let x be a...Ch. 6.4 - Let A be an Hermitian matrix and let B=iA. Show...Ch. 6.4 - Let A and C be matrices in mn and let Bnr. Prove...Ch. 6.4 - Prob. 10ECh. 6.4 - Show that z,w=wHz defines an inner product on n.Ch. 6.4 - Let x, y, and z be vectors in n and let and be...Ch. 6.4 - Let {u1,...,un} be an orthonormal basis for a...Ch. 6.4 - Given that A=(40001i0 i1) find a matrix B such...Ch. 6.4 - Let U be a unitary matrix. Prove that U is normal....Ch. 6.4 - Let u be a unit vector in n and define U=I2uuH....Ch. 6.4 - Show that if a matrix U is both unitary and...Ch. 6.4 - Let A be a 22 matrix with Schur decomposition UTUH...Ch. 6.4 - Let A be a 55 matrix with real entries. Let A=QTQT...Ch. 6.4 - Let A be a nn matrix with Schur decomposition...Ch. 6.4 - Show that M=A+iB (where A and B are real matrices)...Ch. 6.4 - Prob. 22ECh. 6.4 - Prob. 23ECh. 6.4 - Prob. 24ECh. 6.4 - Prob. 25ECh. 6.4 - Let A be a Hermitian matrix with eigenvalues...Ch. 6.4 - Let A=(0110) Write A as a sum 1u1u1T+2u2u2T, where...Ch. 6.4 - Let A be a Hermitian matrix with eigenvalues 12n...Ch. 6.4 - Given Amm,Bnn,Cmn, the equation AXXB=C(3) is known...Ch. 6.5 - Show that A and AT have the same nonzero singular...Ch. 6.5 - Use the method of Example 1 to find the singular...Ch. 6.5 - For each of the matrices in Exercise 2: determine...Ch. 6.5 - Let A=( 28 20 14 19 102 21)=( 3 5 4 5 0 4 5 3 5...Ch. 6.5 - The matrix A=(254630630254) has singular value...Ch. 6.5 - Prove that if A is a symmetric matrix with...Ch. 6.5 - Let A be an mn matrix with singular value...Ch. 6.5 - Let A be an nn matrix. Show that ATA and AAT are...Ch. 6.5 - Let A be an nn matrix with singular values...Ch. 6.5 - Let A be an nn matrix with singular value...Ch. 6.5 - Show that if is a singular value of A then there...Ch. 6.5 - Let A be an mn matrix of rank n with singular...Ch. 6.5 - Prob. 13ECh. 6.6 - Find the matrix associated with each of the...Ch. 6.6 - Reorder the eigenvalues in Example 2 so that 1=4...Ch. 6.6 - Prob. 3ECh. 6.6 - Let 1 and 2 be the eigenvalues of A=(abbc) What...Ch. 6.6 - Prob. 5ECh. 6.6 - Which of the matrices that follow are positive...Ch. 6.6 - For each of the following functions, determine...Ch. 6.6 - Show that if A is symmetric positive definite,...Ch. 6.6 - Prob. 9ECh. 6.6 - Prob. 10ECh. 6.6 - Let A be a symmetric nn matrix with eigenvalues...Ch. 6.6 - Prob. 12ECh. 6.6 - Prob. 13ECh. 6.6 - Let A be a symmetric positive definite nn matrix....Ch. 6.7 - For each of the following matrices, compute the...Ch. 6.7 - Prob. 2ECh. 6.7 - Let A=(2 100 12 100 12 100 12) Compute the LU...Ch. 6.7 - For each of the following, factor the given matrix...Ch. 6.7 - Find the Cholesky decomposition LLT for each of...Ch. 6.7 - Prob. 6ECh. 6.7 - Prove each of the following: If U is a unit upper...Ch. 6.7 - Prob. 8ECh. 6.7 - Let A be a symmetric positive definite matrix with...Ch. 6.7 - Let A be an mn matrix with rank n. Show that the...Ch. 6.7 - Prob. 11ECh. 6.7 - Let A be a symmetric positive definite matrix and...Ch. 6.7 - Prob. 13ECh. 6.7 - Prob. 14ECh. 6.7 - Prob. 15ECh. 6.7 - Let A be an nn symmetric negative definite matrix....Ch. 6.7 - Prob. 17ECh. 6.8 - Find the eigenvalues of each of the following...Ch. 6.8 - Prob. 2ECh. 6.8 - Find the output vector x in the open version of...Ch. 6.8 - Consider the closed version of the Leontief...Ch. 6.8 - Prob. 5ECh. 6.8 - Prob. 6ECh. 6.8 - Which of the matrices that follow are reducible?...Ch. 6.8 - Prob. 8ECh. 6.8 - Prob. 9ECh. 6.8 - Prove that a 22 matrix A is reducible if and only...Ch. 6.8 - Prove the Forbenius theorem in the case where A is...Ch. 6.8 - Prob. 12ECh. 6.8 - Let A be an nn positive stochastic matrix with...Ch. 6.8 - Would the results of parts (c) and (d) in Exercise...Ch. 6.8 - A management student received fellowship offers...Ch. 6 - The top matrix on the menu is the diagonal matrix...Ch. 6 - Prob. 2ECh. 6 - Prob. 3ECh. 6 - Prob. 4ECh. 6 - Prob. 5ECh. 6 - Prob. 6ECh. 6 - Prob. 7ECh. 6 - The last item on the eigshow menu will generate a...Ch. 6 - Prob. 9ECh. 6 - Prob. 10ECh. 6 - Prob. 11ECh. 6 - Consider the matrices A=(5 33 5) and B=(5 335)...Ch. 6 - Prob. 13ECh. 6 - Prob. 14ECh. 6 - Prob. 15ECh. 6 - Prob. 16ECh. 6 - Prob. 17ECh. 6 - Prob. 18ECh. 6 - Prob. 19ECh. 6 - Let A be a nonsingular 22 matrix with singular...Ch. 6 - Set A=[1,1;0.5,0.5] and use MATLAB to verify each...Ch. 6 - Prob. 22ECh. 6 - Prob. 23ECh. 6 - Prob. 24ECh. 6 - Prob. 25ECh. 6 - If A is an nn matrix whose eigenvalues are all...Ch. 6 - If A is nn matrix, then A and AT have the same...Ch. 6 - If A and B are similar matrices, then they have...Ch. 6 - If A and B are nn matrices with the same...Ch. 6 - If A has eigenvalues of multiplicity greater than...Ch. 6 - If A is a 44 matrix of rank 3 and =0 is an...Ch. 6 - If A is a 44 matrix of rank 1 and =0 is an...Ch. 6 - The rank of an nn matrix A is equal to the number...Ch. 6 - The rank of an mn matrix A is equal to the number...Ch. 6 - If A is Hermitian and c is a complex scalar, then...Ch. 6 - If an nn matrix A has Schur decomposition A=UTUH,...Ch. 6 - If A is normal, but not Hermitian, then A must...Ch. 6 - Prob. 13CTACh. 6 - Prob. 14CTACh. 6 - If A is symmetric, then eA is symmetric positive...Ch. 6 - Let A=(10011 112 2) Find the eigenvalues of A. For...Ch. 6 - Let A be a 44 matrix with real entries that has...Ch. 6 - Let A be a nonsingular nn matrix and let be an...Ch. 6 - Show that if A is a matrix of the form...Ch. 6 - Let A=(4222 10 102 10 14) Without computing the...Ch. 6 - Prob. 6CTBCh. 6 - Prob. 7CTBCh. 6 - Let A be a 44 real symmetric matrix with...Ch. 6 - Let {u1,u2} be an orthonormal basis for 2 and...Ch. 6 - Let A be a 55 nonsymmetric matrix with rank equal...Ch. 6 - Let A and B be nn matrices. If A is real and...Ch. 6 - Let A be a matrix whose singular value...
Additional Math Textbook Solutions
Find more solutions based on key concepts
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
The first derivative of function y=25x4.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
147. Draining a tank Water drains from the conical tank shown in the accompanying figure at the rate .
a. What...
University Calculus
Empirical versus Theoretical A Monopoly player claims that the probability of getting a 4 when rolling a six-si...
Introductory Statistics
Let F be a continuous distribution function. If U is uniformly distributed on (0,1), find the distribution func...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Question 5. Let A, B, C ben x n-matrices, S is nonsigular. If A = S-1 BS, show that det (A) = det (B) Question 6. For what values of k is the matrix A = (2- k -1 -1 2) singular? karrow_forward1 4 5 Question 3. Find A-1 (if exists), where A = -3 -1 -2 2 3 4 Question 4. State 4 equivalent conditions for a matrix A to be nonsingulararrow_forwardHow long is a guy wire reaching from the top of a 15-foot pole to a point on the ground 9-feet from the pole? Question content area bottom Part 1 The guy wire is exactly feet long. (Type an exact answer, using radicals as needed.) Part 2 The guy wire is approximatelyfeet long. (Round to the nearest thousandth.)arrow_forward
- Question 6 Not yet answered Marked out of 5.00 Flag question = If (4,6,-11) and (-12,-16,4), = Compute the cross product vx w karrow_forwardConsider the following vector field v^-> (x,y): v^->(x,y)=2yi−xj What is the magnitude of the vector v⃗ located in point (13,9)? [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places]arrow_forwardQuestion 4 Find the value of the first element for the first row of the inverse matrix of matrix B. 3 Not yet answered B = Marked out of 5.00 · (³ ;) Flag question 7 [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places] Answer:arrow_forward
- Question 2 Not yet answered Multiply the following Matrices together: [77-4 A = 36 Marked out of -5 -5 5.00 B = 3 5 Flag question -6 -7 ABarrow_forwardAssume {u1, U2, u3, u4} does not span R³. Select the best statement. A. {u1, U2, u3} spans R³ if u̸4 is a linear combination of other vectors in the set. B. We do not have sufficient information to determine whether {u₁, u2, u3} spans R³. C. {U1, U2, u3} spans R³ if u̸4 is a scalar multiple of another vector in the set. D. {u1, U2, u3} cannot span R³. E. {U1, U2, u3} spans R³ if u̸4 is the zero vector. F. none of the abovearrow_forwardSelect the best statement. A. If a set of vectors includes the zero vector 0, then the set of vectors can span R^ as long as the other vectors are distinct. n B. If a set of vectors includes the zero vector 0, then the set of vectors spans R precisely when the set with 0 excluded spans Rª. ○ C. If a set of vectors includes the zero vector 0, then the set of vectors can span Rn as long as it contains n vectors. ○ D. If a set of vectors includes the zero vector 0, then there is no reasonable way to determine if the set of vectors spans Rn. E. If a set of vectors includes the zero vector 0, then the set of vectors cannot span Rn. F. none of the abovearrow_forward
- Which of the following sets of vectors are linearly independent? (Check the boxes for linearly independent sets.) ☐ A. { 7 4 3 13 -9 8 -17 7 ☐ B. 0 -8 3 ☐ C. 0 ☐ D. -5 ☐ E. 3 ☐ F. 4 THarrow_forward3 and = 5 3 ---8--8--8 Let = 3 U2 = 1 Select all of the vectors that are in the span of {u₁, u2, u3}. (Check every statement that is correct.) 3 ☐ A. The vector 3 is in the span. -1 3 ☐ B. The vector -5 75°1 is in the span. ГОЛ ☐ C. The vector 0 is in the span. 3 -4 is in the span. OD. The vector 0 3 ☐ E. All vectors in R³ are in the span. 3 F. The vector 9 -4 5 3 is in the span. 0 ☐ G. We cannot tell which vectors are i the span.arrow_forward(20 p) 1. Find a particular solution satisfying the given initial conditions for the third-order homogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y(3)+2y"-y-2y = 0; y(0) = 1, y'(0) = 2, y"(0) = 0; y₁ = e*, y2 = e¯x, y3 = e−2x (20 p) 2. Find a particular solution satisfying the given initial conditions for the second-order nonhomogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y"-2y-3y = 6; y(0) = 3, y'(0) = 11 yc = c₁ex + c2e³x; yp = −2 (60 p) 3. Find the general, and if possible, particular solutions of the linear systems of differential equations given below using the eigenvalue-eigenvector method. (See Section 7.3 in your textbook if you need a review of the subject.) = a) x 4x1 + x2, x2 = 6x1-x2 b) x=6x17x2, x2 = x1-2x2 c) x = 9x1+5x2, x2 = −6x1-2x2; x1(0) = 1, x2(0)=0arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Orthogonality in Inner Product Spaces; Author: Study Force;https://www.youtube.com/watch?v=RzIx_rRo9m0;License: Standard YouTube License, CC-BY
Abstract Algebra: The definition of a Group; Author: Socratica;https://www.youtube.com/watch?v=QudbrUcVPxk;License: Standard Youtube License