Single Variable Calculus: Early Transcendentals, Books a la Carte, and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition)
Single Variable Calculus: Early Transcendentals, Books a la Carte, and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition)
3rd Edition
ISBN: 9780134996103
Author: William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher: PEARSON
bartleby

Videos

Textbook Question
Book Icon
Chapter 6.2, Problem 15E

Finding area Determine the area of the shaded region in the following figures.

15.   

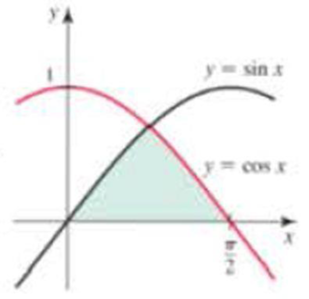
Chapter 6.2, Problem 15E, Finding area Determine the area of the shaded region in the following figures. 15.

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 6.2, Problem 14E
Next
Chapter 6.2, Problem 16E
Students have asked these similar questions
A function is defined on the interval (-π/2,π/2) by this multipart rule: if -π/2 < x < 0 f(x) = a if x=0 31-tan x +31-cot x if 0 < x < π/2 Here, a and b are constants. Find a and b so that the function f(x) is continuous at x=0. a= b= 3
Use the definition of continuity and the properties of limits to show that the function is continuous at the given number a. f(x) = (x + 4x4) 5, a = -1 lim f(x) X--1 = lim x+4x X--1 lim X-1 4 x+4x 5 ))" 5 )) by the power law by the sum law lim (x) + lim X--1 4 4x X-1 -(0,00+( Find f(-1). f(-1)=243 lim (x) + -1 +4 35 4 ([ ) lim (x4) 5 x-1 Thus, by the definition of continuity, f is continuous at a = -1. by the multiple constant law by the direct substitution property
1. Compute Lo F⚫dr, where and C is defined by F(x, y) = (x² + y)i + (y − x)j r(t) = (12t)i + (1 − 4t + 4t²)j from the point (1, 1) to the origin.

Chapter 6 Solutions

Single Variable Calculus: Early Transcendentals, Books a la Carte, and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition)

Ch. 6.1 - A police officer leaves his station on a...Ch. 6.1 - Describe a possible motion of an object along a...Ch. 6.1 - Is the position s(t) a number or a function? For...Ch. 6.1 - Without doing further calculations, what are the...Ch. 6.1 - Prob. 5QCCh. 6.1 - Prob. 6QCCh. 6.1 - Explain the meaning of position, displacement, and...Ch. 6.1 - Suppose the velocity of an object moving along a...Ch. 6.1 - Given the velocity function v of an object moving...Ch. 6.1 - Prob. 4E
Ch. 6.1 - Prob. 5ECh. 6.1 - What is the result of integrating a population...Ch. 6.1 - Displacement and distance from velocity Consider...Ch. 6.1 - Displacement and distance from velocity Consider...Ch. 6.1 - Velocity graphs The figures show velocity...Ch. 6.1 - Prob. 10ECh. 6.1 - Prob. 11ECh. 6.1 - Prob. 12ECh. 6.1 - Displacement from velocity Consider an object...Ch. 6.1 - Displacement from velocity Consider an object...Ch. 6.1 - Displacement from velocity Consider an object...Ch. 6.1 - Displacement from velocity Assume t is time...Ch. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Prob. 18ECh. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Prob. 20ECh. 6.1 - Prob. 21ECh. 6.1 - Prob. 22ECh. 6.1 - Prob. 23ECh. 6.1 - Prob. 24ECh. 6.1 - Flying into a headwind The velocity (in mi/hr) of...Ch. 6.1 - Day hike The velocity (in mi/hr) of a hiker...Ch. 6.1 - Piecewise velocity The velocity of a (fast)...Ch. 6.1 - Probe speed A data collection probe is dropped...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Prob. 31ECh. 6.1 - Prob. 32ECh. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Prob. 34ECh. 6.1 - Prob. 35ECh. 6.1 - Prob. 36ECh. 6.1 - Prob. 37ECh. 6.1 - Prob. 38ECh. 6.1 - Prob. 39ECh. 6.1 - Prob. 40ECh. 6.1 - Prob. 41ECh. 6.1 - Prob. 42ECh. 6.1 - Population growth 43. A culture of bacteria in a...Ch. 6.1 - Prob. 44ECh. 6.1 - Oil production An oil refinery produces oil at a...Ch. 6.1 - Prob. 46ECh. 6.1 - Prob. 47ECh. 6.1 - Prob. 48ECh. 6.1 - Prob. 49ECh. 6.1 - Prob. 50ECh. 6.1 - Prob. 51ECh. 6.1 - Prob. 52ECh. 6.1 - Prob. 53ECh. 6.1 - Prob. 54ECh. 6.1 - Prob. 55ECh. 6.1 - Prob. 56ECh. 6.1 - Marginal cost Consider the following marginal cost...Ch. 6.1 - Prob. 58ECh. 6.1 - Explain why or why not Determine whether the...Ch. 6.1 - Prob. 60ECh. 6.1 - Prob. 61ECh. 6.1 - Prob. 62ECh. 6.1 - Prob. 63ECh. 6.1 - Prob. 64ECh. 6.1 - Prob. 65ECh. 6.1 - Prob. 66ECh. 6.1 - Prob. 67ECh. 6.1 - Variable gravity At Earths surface, the...Ch. 6.1 - Prob. 69ECh. 6.1 - Prob. 70ECh. 6.1 - Another look at the Fundamental Theorem 71. Use...Ch. 6.1 - Prob. 72ECh. 6.2 - In the area formula for a region between two...Ch. 6.2 - Prob. 2QCCh. 6.2 - Prob. 3QCCh. 6.2 - Prob. 4QCCh. 6.2 - Set up a sum of two integrals that equals the area...Ch. 6.2 - Set up an integral that equals the area of the...Ch. 6.2 - Make a sketch to show a case in which the area...Ch. 6.2 - Make a sketch to show a case in which the area...Ch. 6.2 - Find the area of the region (see figure) in two...Ch. 6.2 - Find the area of the region (see figure) in two...Ch. 6.2 - Express the area of the shaded region in Exercise...Ch. 6.2 - Prob. 8ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 10ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 12ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 14ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 16ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 18ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 22ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 24ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 26ECh. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Prob. 30ECh. 6.2 - Prob. 31ECh. 6.2 - Prob. 32ECh. 6.2 - Area between velocity curves Two runners, starting...Ch. 6.2 - Prob. 34ECh. 6.2 - Prob. 35ECh. 6.2 - Calculus and geometry For the given regions R1 and...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Prob. 38ECh. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Prob. 44ECh. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Prob. 47ECh. 6.2 - Prob. 48ECh. 6.2 - Any method Use any method (including geometry) to...Ch. 6.2 - Prob. 50ECh. 6.2 - Prob. 51ECh. 6.2 - Prob. 52ECh. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Prob. 56ECh. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Prob. 58ECh. 6.2 - Prob. 59ECh. 6.2 - Prob. 60ECh. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Prob. 62ECh. 6.2 - Prob. 63ECh. 6.2 - Prob. 64ECh. 6.2 - Prob. 65ECh. 6.2 - Prob. 66ECh. 6.2 - Prob. 67ECh. 6.2 - Prob. 68ECh. 6.2 - Prob. 69ECh. 6.2 - Prob. 70ECh. 6.2 - Prob. 71ECh. 6.2 - Prob. 72ECh. 6.2 - Prob. 73ECh. 6.2 - Prob. 74ECh. 6.2 - Prob. 75ECh. 6.2 - Prob. 76ECh. 6.2 - Prob. 77ECh. 6.2 - Prob. 78ECh. 6.3 - Why is the volume as given by the general slicing...Ch. 6.3 - In Example 2 what is the cross-sectional area...Ch. 6.3 - What solid results when the region R is revolved...Ch. 6.3 - Prob. 4QCCh. 6.3 - Prob. 5QCCh. 6.3 - Prob. 6QCCh. 6.3 - Suppose a cut is made through a solid object...Ch. 6.3 - A solid has a circular base and cross sections...Ch. 6.3 - Consider a solid whose base is the region in the...Ch. 6.3 - Why is the disk method a special case of the...Ch. 6.3 - Prob. 5ECh. 6.3 - Prob. 6ECh. 6.3 - Use the region R that is bounded by the graphs of...Ch. 6.3 - Use the region R that is bounded by the graphs of...Ch. 6.3 - Use the region R that is bounded by the graphs of...Ch. 6.3 - Prob. 10ECh. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - Prob. 16ECh. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Prob. 30ECh. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Which is greater? For the following regions R,...Ch. 6.3 - Which is greater? For the following regions R,...Ch. 6.3 - Prob. 47ECh. 6.3 - Prob. 48ECh. 6.3 - Revolution about other axes Let R be the region...Ch. 6.3 - Prob. 50ECh. 6.3 - Revolution about other axes Let R be the region...Ch. 6.3 - Prob. 52ECh. 6.3 - Prob. 53ECh. 6.3 - Prob. 54ECh. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Prob. 57ECh. 6.3 - Prob. 58ECh. 6.3 - Prob. 59ECh. 6.3 - Prob. 60ECh. 6.3 - Prob. 61ECh. 6.3 - Prob. 62ECh. 6.3 - Prob. 63ECh. 6.3 - Prob. 64ECh. 6.3 - Prob. 65ECh. 6.3 - Prob. 66ECh. 6.3 - Prob. 67ECh. 6.3 - Volume of a wooden object A solid wooden object...Ch. 6.3 - Prob. 69ECh. 6.3 - Water in a bowl A hemispherical bowl of radius 8...Ch. 6.3 - Prob. 71ECh. 6.3 - Prob. 72ECh. 6.3 - Cavalieris principle Cavalieris principle states...Ch. 6.3 - Prob. 74ECh. 6.4 - The triangle bounded by the x-axis, the line y =...Ch. 6.4 - Prob. 2QCCh. 6.4 - Prob. 3QCCh. 6.4 - Assume f and g are continuous with f(x) g(x) on...Ch. 6.4 - Fill in the blanks: A region R is revolved about...Ch. 6.4 - Fill in the blanks: A region R is revolved about...Ch. 6.4 - Look again at the region R in Figure 6.38 (p 439)....Ch. 6.4 - Let R be the region in the first quadrant bounded...Ch. 6.4 - Let R be the region bounded by the curves...Ch. 6.4 - Prob. 7ECh. 6.4 - Let R be the region bounded by the curves...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 10ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 12ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 14ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 16ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 18ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 20ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 25ECh. 6.4 - Prob. 26ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 28ECh. 6.4 - Prob. 29ECh. 6.4 - Prob. 30ECh. 6.4 - Prob. 31ECh. 6.4 - Prob. 32ECh. 6.4 - Prob. 33ECh. 6.4 - Prob. 34ECh. 6.4 - Washers vs. shells Let R be the region bounded by...Ch. 6.4 - Prob. 36ECh. 6.4 - Washers vs. shells Let R be the region bounded by...Ch. 6.4 - Prob. 38ECh. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Prob. 40ECh. 6.4 - Prob. 41ECh. 6.4 - Prob. 42ECh. 6.4 - Prob. 43ECh. 6.4 - Prob. 44ECh. 6.4 - Prob. 45ECh. 6.4 - Prob. 46ECh. 6.4 - Prob. 47ECh. 6.4 - Prob. 48ECh. 6.4 - Volume of a sphere Let R be the region bounded by...Ch. 6.4 - Prob. 50ECh. 6.4 - A torus (doughnut) A torus is formed when a circle...Ch. 6.4 - Prob. 52ECh. 6.4 - Prob. 53ECh. 6.4 - Prob. 54ECh. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Prob. 56ECh. 6.4 - Prob. 57ECh. 6.4 - Prob. 58ECh. 6.4 - Choose your method Let R be the region bounded by...Ch. 6.4 - Prob. 60ECh. 6.4 - Choose your method Let R be the region bounded by...Ch. 6.4 - Prob. 62ECh. 6.4 - Prob. 63ECh. 6.4 - Prob. 64ECh. 6.4 - Prob. 65ECh. 6.4 - Prob. 66ECh. 6.4 - Prob. 67ECh. 6.4 - Prob. 68ECh. 6.4 - Prob. 69ECh. 6.4 - Prob. 70ECh. 6.4 - Prob. 71ECh. 6.4 - Equal integrals Without evaluating integrals,...Ch. 6.4 - Volumes without calculus Solve the following...Ch. 6.4 - Prob. 74ECh. 6.4 - Prob. 75ECh. 6.4 - Prob. 76ECh. 6.5 - What does the arc length formula give for the...Ch. 6.5 - Prob. 2QCCh. 6.5 - Prob. 3QCCh. 6.5 - Prob. 1ECh. 6.5 - Prob. 2ECh. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Prob. 6ECh. 6.5 - Prob. 7ECh. 6.5 - Prob. 8ECh. 6.5 - Arc lezngth calculations Find the arc length of...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Prob. 22ECh. 6.5 - Prob. 23ECh. 6.5 - Prob. 24ECh. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Prob. 28ECh. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a.Write and simplify the...Ch. 6.5 - Prob. 31ECh. 6.5 - Prob. 32ECh. 6.5 - Explain why or why not Determine whether the...Ch. 6.5 - Prob. 34ECh. 6.5 - Functions from arc length What differentiable...Ch. 6.5 - Function from arc length Find a curve that passes...Ch. 6.5 - Prob. 37ECh. 6.5 - Prob. 38ECh. 6.5 - Prob. 39ECh. 6.5 - Prob. 40ECh. 6.5 - Prob. 41ECh. 6.5 - Bernoullis parabolas Johann Bernoulli (16671748)...Ch. 6.6 - Which is greater the surface area of a cone of...Ch. 6.6 - Prob. 2QCCh. 6.6 - Prob. 3QCCh. 6.6 - Prob. 1ECh. 6.6 - Prob. 2ECh. 6.6 - Prob. 3ECh. 6.6 - Prob. 4ECh. 6.6 - Prob. 5ECh. 6.6 - Prob. 6ECh. 6.6 - Prob. 7ECh. 6.6 - Prob. 8ECh. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Revolving about the y-axis Find the area of the...Ch. 6.6 - Prob. 12ECh. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Prob. 14ECh. 6.6 - Prob. 15ECh. 6.6 - Prob. 16ECh. 6.6 - Prob. 17ECh. 6.6 - Prob. 18ECh. 6.6 - Prob. 19ECh. 6.6 - Prob. 20ECh. 6.6 - Painting surfaces A 1.5-mm layer of paint is...Ch. 6.6 - Prob. 22ECh. 6.6 - Explain why or why not Determine whether the...Ch. 6.6 - T 2629. Surface area using technology Consider the...Ch. 6.6 - T 2629. Surface area using technology Consider the...Ch. 6.6 - Surface area using technology Consider the...Ch. 6.6 - Surface area using technology Consider the...Ch. 6.6 - Surface area using technology Consider the...Ch. 6.6 - Revolving an astroid Consider the upper half of...Ch. 6.6 - Prob. 30ECh. 6.6 - Prob. 31ECh. 6.6 - Prob. 32ECh. 6.6 - Prob. 33ECh. 6.6 - Prob. 34ECh. 6.6 - Prob. 35ECh. 6.6 - Prob. 36ECh. 6.6 - Prob. 37ECh. 6.6 - Prob. 38ECh. 6.6 - Surface-area-to-volume ratio (SAV) In the design...Ch. 6.6 - Prob. 40ECh. 6.6 - Prob. 41ECh. 6.6 - Surface plus cylinder Suppose f is a nonnegative...Ch. 6.7 - In Figure 6.69, suppose a = 0, b = 3, and the...Ch. 6.7 - Prob. 2QCCh. 6.7 - Prob. 3QCCh. 6.7 - Prob. 4QCCh. 6.7 - In Example 3b, the bucket occupies the interval...Ch. 6.7 - Prob. 6QCCh. 6.7 - Prob. 7QCCh. 6.7 - Suppose a 1-m cylindrical bar has a constant...Ch. 6.7 - Explain how to find the mass of a one-dimensional...Ch. 6.7 - How much work is required to move an object from x...Ch. 6.7 - Why is integration used to find the work done by a...Ch. 6.7 - Why is integration used to find the work required...Ch. 6.7 - Prob. 6ECh. 6.7 - What is the pressure on a horizontal surface with...Ch. 6.7 - Prob. 8ECh. 6.7 - Consider the cylindrical tank in Example 4 that...Ch. 6.7 - Consider the cylindrical tank in Example 4 that...Ch. 6.7 - Consider the cylindrical tank in Example 4 that...Ch. 6.7 - Prob. 12ECh. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Prob. 16ECh. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Prob. 20ECh. 6.7 - Work from force How much work is required to move...Ch. 6.7 - Prob. 22ECh. 6.7 - Compressing and stretching a spring Suppose a...Ch. 6.7 - Compressing and stretching a spring Suppose a...Ch. 6.7 - Prob. 25ECh. 6.7 - Prob. 26ECh. 6.7 - Prob. 27ECh. 6.7 - Prob. 28ECh. 6.7 - Calculating work for different springs Calculate...Ch. 6.7 - Prob. 30ECh. 6.7 - Winding a chain A 30-m-long chain hangs vertically...Ch. 6.7 - Prob. 32ECh. 6.7 - Winding part of a chain A 20-m-long, 50-kg chain...Ch. 6.7 - Leaky Bucket A 1-kg bucket resting on the ground...Ch. 6.7 - Emptying a swimming pool A swimming pool has the...Ch. 6.7 - Prob. 36ECh. 6.7 - Emptying a half-full cylindrical tank Suppose the...Ch. 6.7 - Prob. 38ECh. 6.7 - Emptying a conical tank A water tank is shaped...Ch. 6.7 - Prob. 40ECh. 6.7 - Filling a spherical tank A spherical water tank...Ch. 6.7 - Emptying a water trough A water trough has a...Ch. 6.7 - Emptying a water trough A cattle trough has a...Ch. 6.7 - Prob. 44ECh. 6.7 - Emptying a conical tank An inverted cone is 2 m...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Prob. 50ECh. 6.7 - Prob. 51ECh. 6.7 - Prob. 52ECh. 6.7 - Prob. 53ECh. 6.7 - Prob. 54ECh. 6.7 - Prob. 55ECh. 6.7 - Prob. 56ECh. 6.7 - Prob. 57ECh. 6.7 - Prob. 58ECh. 6.7 - Prob. 59ECh. 6.7 - Prob. 60ECh. 6.7 - Prob. 61ECh. 6.7 - Prob. 62ECh. 6.7 - Drinking juice A glass has circular cross sections...Ch. 6.7 - Prob. 64ECh. 6.7 - Prob. 65ECh. 6.7 - Prob. 66ECh. 6.7 - Prob. 67ECh. 6.7 - Work by two different integrals A rigid body with...Ch. 6.7 - Work in a gravitational field For large distances...Ch. 6.7 - Prob. 70ECh. 6 - Explain why or why not Determine whether the...Ch. 6 - Prob. 2RECh. 6 - Prob. 3RECh. 6 - Prob. 4RECh. 6 - Prob. 5RECh. 6 - Prob. 6RECh. 6 - Prob. 7RECh. 6 - Prob. 8RECh. 6 - Prob. 9RECh. 6 - Prob. 10RECh. 6 - Prob. 11RECh. 6 - Prob. 12RECh. 6 - Prob. 13RECh. 6 - Prob. 14RECh. 6 - Prob. 15RECh. 6 - Prob. 16RECh. 6 - Prob. 17RECh. 6 - Prob. 18RECh. 6 - Prob. 19RECh. 6 - Prob. 20RECh. 6 - Prob. 21RECh. 6 - Prob. 22RECh. 6 - Prob. 23RECh. 6 - Prob. 24RECh. 6 - Prob. 25RECh. 6 - Prob. 26RECh. 6 - Prob. 27RECh. 6 - Multiple regions The regions R1, R2, and R3 (see...Ch. 6 - Prob. 29RECh. 6 - Prob. 30RECh. 6 - Prob. 31RECh. 6 - Prob. 32RECh. 6 - Prob. 33RECh. 6 - Prob. 34RECh. 6 - Prob. 35RECh. 6 - Area and volume Let R be the region in the first...Ch. 6 - Prob. 37RECh. 6 - Prob. 38RECh. 6 - Prob. 39RECh. 6 - Prob. 40RECh. 6 - Prob. 41RECh. 6 - Prob. 42RECh. 6 - Prob. 43RECh. 6 - Prob. 44RECh. 6 - Prob. 45RECh. 6 - Prob. 46RECh. 6 - Prob. 47RECh. 6 - Prob. 48RECh. 6 - Prob. 49RECh. 6 - Prob. 50RECh. 6 - Prob. 51RECh. 6 - Prob. 52RECh. 6 - Prob. 53RECh. 6 - Prob. 54RECh. 6 - Prob. 55RECh. 6 - Prob. 56RECh. 6 - Prob. 57RECh. 6 - Prob. 58RECh. 6 - Prob. 59RECh. 6 - Prob. 60RECh. 6 - Prob. 61RECh. 6 - Prob. 62RECh. 6 - Prob. 63RECh. 6 - Prob. 64RECh. 6 - Prob. 65RECh. 6 - Surface area and volume Let f(x)=13x3 and let R be...Ch. 6 - Surface area and volume Let f(x)=3xx2 and let R be...Ch. 6 - Prob. 68RECh. 6 - Surface area and more Let f(x)=x42+116x2 and let R...Ch. 6 - Prob. 70RECh. 6 - Prob. 71RECh. 6 - Prob. 72RECh. 6 - Prob. 73RECh. 6 - Leaky bucket A 1-kg bucket resting on the ground...Ch. 6 - Prob. 75RECh. 6 - Prob. 76RECh. 6 - Pumping water A water tank has the shape of a box...Ch. 6 - Prob. 78RECh. 6 - Prob. 79RECh. 6 - Prob. 80RECh. 6 - Prob. 81RECh. 6 - Prob. 82RECh. 6 - Fluid Forces Suppose the Mowing plates are placed...Ch. 6 - Prob. 84RECh. 6 - Prob. 85RECh. 6 - Prob. 86RE
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
PREALGEBRA
Algebra
ISBN:9781938168994
Author:OpenStax
Publisher:OpenStax
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
SEE MORE TEXTBOOKS
Problems on Area and Circumference of Circle| Basics of Circle| Questions on Circle||BrainPanthers; Author: Brain Panthers;https://www.youtube.com/watch?v=RcNEL9OzcC0;License: Standard YouTube License, CC-BY