HEART OF MATHEMATICS
4th Edition
ISBN: 9781119760061
Author: Burger
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6.1, Problem 8MS
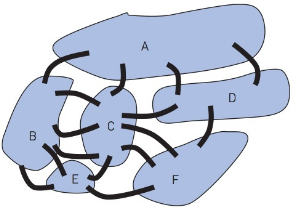
Linking the loops. In this map, the following walks can be taken from various starting points: CAADDEFC, FCCBB CCEEF, DCCBBEEBBAAD. Can these walks be spliced together to create one walk that starts on landmass C, crosses each bridge exactly once, and then returns to C? If so, find such a walk. If not, explain why not.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
=
2.035
765 03
-9 ws 64
7 sin &3-9sin 04 = 1.134
The diagram below models the layout at a carnival where G, R, P, C, B, and E are various locations on the grounds. GRPC is a parallelogram.
19
G
R
375 ft
425 ft
325 ft
B 225 ft
P
E
Part A: Identify a pair of similar triangles. (2 points)
Part B: Explain how you know the triangles from Part A are similar. (4 points)
Part C: Find the distance from B to E and from P to E. Show your work. (4 points)
Solve for theta 3 and 4
Chapter 6 Solutions
HEART OF MATHEMATICS
Ch. 6.1 - Map maker, map maker make me a graph. Represent...Ch. 6.1 - Unabridged list. Represent cach landmass from...Ch. 6.1 - Will the walk work? Does your graph from...Ch. 6.1 - Walk around the house. Is it possibel to traverse...Ch. 6.1 - Walk the line. Does this graph above have an Euler...Ch. 6.1 - Walkabout. Does this graph have an Euler circuit?...Ch. 6.1 - Linking the loops. In this map, the following...Ch. 6.1 - Scenic drive. (S) Here is a map of Rockystone...Ch. 6.1 - Under-edged. (H) Does this graph have an Euler...Ch. 6.1 - No man is an island. The country of Pelago...
Ch. 6.1 - Path-o-rama. For each graph below, determine if...Ch. 6.1 - Walk around the block. Create a graph of the...Ch. 6.1 - Walking the dogs. Your dogs, Abbey and Bear, love...Ch. 6.1 - Delivery query. The next time you see a postal...Ch. 6.1 - Snow job. (ExH) Shown here is a map of the tiny...Ch. 6.1 - Special delivery. (ExH) Julia is the letter...Ch. 6.1 - Draw this old house. Suppose you wanted to trace...Ch. 6.1 - Path of no return. Consider this map showing a...Ch. 6.1 - Without a trace. Is it possibel to trace out...Ch. 6.1 - New Euler. In the three previous Mindscapes, you...Ch. 6.1 - New edge—new circuit. Look at the graph for...Ch. 6.1 - New edge—new path. Review your work for...Ch. 6.1 - Path to proof. Suppose you have a connected graph...Ch. 6.1 - No Euler no how. Look at graph (a) for Mindscape...Ch. 6.1 - Degree day. (S) For cach graph below, determine...Ch. 6.1 - degrees of proof. Review your work for Mindscape...Ch. 6.1 - Degrees in sequence. Can you draw a graph that has...Ch. 6.1 - Even Steven. Review your work in Mindscape 28 to...Ch. 6.1 - Little League lesson. (H) You are in charge of...Ch. 6.1 - With a group of folks. In a small group, discuss...Ch. 6.1 - Power beyond the mathematics. Provide several...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.2 - What a character! What expression gives the Euler...Ch. 6.2 - Count, then verify. What are the values of V, E,...Ch. 6.2 - Sneeze, then verify. Look at an unopened tissue...Ch. 6.2 - Blow, then verify. Inflate a ballon and use a...Ch. 6.2 - Add one. Find the values V, E, and F for the graph...Ch. 6.2 - Bowling. What is the Euler Characteristic of the...Ch. 6.2 - Making change. We begin with the graph pictured at...Ch. 6.2 - Making a point. Take a connected graph and add a...Ch. 6.2 - On the edge (H). Is it possible to add an edge to...Ch. 6.2 - Soap films. Consider the following sequence of...Ch. 6.2 - Dualing. What is the relationship between the...Ch. 6.2 - Prob. 12MSCh. 6.2 - Lots of separation. Suppose we are told that a...Ch. 6.2 - Prob. 14MSCh. 6.2 - Psychic readings. Someone is thinking of a...Ch. 6.2 - Prob. 16MSCh. 6.2 - Prob. 17MSCh. 6.2 - Circular reasoning. Create a connected graph as...Ch. 6.2 - Prob. 19MSCh. 6.2 - More circles. Consider the sphere described in...Ch. 6.2 - In the rough (S). Count the number of facets,...Ch. 6.2 - Cutting corners (H). The following collection of...Ch. 6.2 - Stellar. The following collection of pictures...Ch. 6.2 - A torus graph (ExH). The Euler Characteristic...Ch. 6.2 - Regular unfolding. Each graph below represents...Ch. 6.2 - A tale of two graphs. Suppose we draw a graph that...Ch. 6.2 - Two graph conjectures (S). Can you conjecture a...Ch. 6.2 - Lots of graphs conjecture. Can you conjecture a...Ch. 6.2 - Torus count. Three hollowed, triangular prisms...Ch. 6.2 - Torus two count (H). Carefully count the number of...Ch. 6.2 - Torus many count. Using the preceding calculations...Ch. 6.2 - Prob. 32MSCh. 6.2 - Tell the truth. Someone said that she made a...Ch. 6.2 - No sphere. Suppose we have a sphere built out of...Ch. 6.2 - Soccer ball. A soccer ball is made of pentagons...Ch. 6.2 - Klein bottle. Using the diagram here for building...Ch. 6.2 - Not many neighbors. Show that every map has at...Ch. 6.2 - Infinite edges. Suppose we consider a conn ected...Ch. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.2 - Prob. 44MSCh. 6.2 - Prob. 45MSCh. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.3 - Dont be cross. Here is a drawing of a graph with...Ch. 6.3 - De Plane! De Plane! (S) Is the graph given in...Ch. 6.3 - Countdown (H). For the graph drawing shown, count...Ch. 6.3 - Prob. 4MSCh. 6.3 - Criss-Cross. Is it possible to redraw the graph...Ch. 6.3 - Dont cross in the edge. Each of the graphs drawn...Ch. 6.3 - Hot crossed buns. Each of the graphs drawn below...Ch. 6.3 - Prob. 8MSCh. 6.3 - Spider on a mirror. Is it possible to redraw the...Ch. 6.3 - One more vertex. The graph here is drawn to show...Ch. 6.3 - Yet one more vertex (H). The graph shown is drawn...Ch. 6.3 - Familiar freckles. Is it possible to redraw the...Ch. 6.3 - Remind you of anyone you know? Is it possible to...Ch. 6.3 - Final countdown. For this graph drawing, count the...Ch. 6.3 - Euler check-up. Use your answer to the previous...Ch. 6.3 - Euler second opinion. For the graph drawing shown...Ch. 6.3 - Prob. 17MSCh. 6.3 - Prob. 18MSCh. 6.3 - A colorful museum. This figure shows the floor...Ch. 6.3 - Limit of 5. Start drawing a planar graph. Keep...Ch. 6.3 - Starring the hexagon. Is it possible to redraw...Ch. 6.3 - Prob. 22MSCh. 6.3 - Prob. 23MSCh. 6.3 - Getting greedy. (H) Suppose you are asked to color...Ch. 6.3 - Stingy rather than greedy. By coloring the...Ch. 6.3 - Getting more colorful. Graphs dont have to be...Ch. 6.3 - Prob. 27MSCh. 6.3 - Prob. 28MSCh. 6.3 - Chromatically applied. There are eight radio...Ch. 6.3 - Prob. 30MSCh. 6.3 - Personal perspectives. Write a short essay...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Prob. 37MSCh. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.4 - Up close and personal. Create a graph to model...Ch. 6.4 - Network lookout. Find an examle of a network...Ch. 6.4 - Prob. 3MSCh. 6.4 - Hamiltonian holiday (S). You are interning for a...Ch. 6.4 - Home style. Create a graph to model the rooms in...Ch. 6.4 - Six degrees or less. Suppose this graph is a model...Ch. 6.4 - Degrees of you. Find ten willing friends or...Ch. 6.4 - Campus shortcut. Find a map of your campus and...Ch. 6.4 - Arborist lesson. Which of the graphs below are...Ch. 6.4 - Prob. 10MSCh. 6.4 - Prob. 11MSCh. 6.4 - Prob. 12MSCh. 6.4 - Prob. 13MSCh. 6.4 - Prob. 14MSCh. 6.4 - Prob. 15MSCh. 6.4 - Hamilton Study. Look at the graph you drew to...Ch. 6.4 - Business trip redux. Look back in the section and...Ch. 6.4 - Handling Hamiltons. For each graph below, find a...Ch. 6.4 - Road trip. You are checking out gradua te programs...Ch. 6.4 - Back to Hatties trip. Look back in this section...Ch. 6.4 - Solve the Icosian Game. Find a Hamiltonian circuit...Ch. 6.4 - Hunt for Hamilton (S). A large island country has...Ch. 6.4 - Has no Hamilton. Give some characteristics that...Ch. 6.4 - Cubing Hamilton (ExH). Can you find a Hamihonian...Ch. 6.4 - Hamiltonian path. A Hamiltonian path is a path in...Ch. 6.4 - Sorry, no path. Give some characteristics that...Ch. 6.4 - Prob. 27MSCh. 6.4 - Prob. 28MSCh. 6.4 - Prob. 29MSCh. 6.4 - Prob. 30MSCh. 6.4 - Edge count. Look at all the trees you drew in the...Ch. 6.4 - Personal perspecthes. Write a short essay...Ch. 6.4 - Prob. 33MSCh. 6.4 - Prob. 34MSCh. 6.4 - Dollars and cents. Your spanning tree has three...Ch. 6.4 - Adding up. Your spanning tree has four edges with...Ch. 6.4 - Prob. 38MSCh. 6.4 - Vertex search (H). Your graph has a Hamiltonian...Ch. 6.4 - Binary gossip tree. You told a secret to two of...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Testing Hypotheses. In Exercises 13-24, assume that a simple random sample has been selected and test the given...
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
Fill in each blank so that the resulting statement is true.
1. A combination of numbers, variables, and opera...
College Algebra (7th Edition)
2. Quantitative Concepts in the News. Identify the major un-resolved issue discussed in today& news. List at th...
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Suppose that 10 fish are caught at a lake that contains 5 distinct types of fish. a. How many different outcome...
A First Course in Probability (10th Edition)
Find the areas of the regions enclosed by the curves in Exercises 83–86.
83. 4x2 + y = 4 and x4 − y = 1
University Calculus: Early Transcendentals (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Given lim x-4 f (x) = 1,limx-49 (x) = 10, and lim→-4 h (x) = -7 use the limit properties to find lim→-4 1 [2h (x) — h(x) + 7 f(x)] : - h(x)+7f(x) 3 O DNEarrow_forwardWrite out and explain your steps for each of the problems.arrow_forward17. Suppose we know that the graph below is the graph of a solution to dy/dt = f(t). (a) How much of the slope field can you sketch from this information? [Hint: Note that the differential equation depends only on t.] (b) What can you say about the solu- tion with y(0) = 2? (For example, can you sketch the graph of this so- lution?) y(0) = 1 y ANarrow_forward
- Write out and explain your steps to each of these problems.arrow_forwardCalculate the area and perimeterarrow_forward65% of all violent felons in the prison system are repeat offenders. If 43 violent felons are randomly selected, find the probability that a. Exactly 28 of them are repeat offenders. b. At most 28 of them are repeat offenders. c. At least 28 of them are repeat offenders. d. Between 22 and 26 (including 22 and 26) of them are repeat offenders.arrow_forward
- (b) Find the (instantaneous) rate of change of y at x = 5. In the previous part, we found the average rate of change for several intervals of decreasing size starting at x = 5. The instantaneous rate of change of fat x = 5 is the limit of the average rate of change over the interval [x, x + h] as h approaches 0. This is given by the derivative in the following limit. lim h→0 - f(x + h) − f(x) h The first step to find this limit is to compute f(x + h). Recall that this means replacing the input variable x with the expression x + h in the rule defining f. f(x + h) = (x + h)² - 5(x+ h) = 2xh+h2_ x² + 2xh + h² 5✔ - 5 )x - 5h Step 4 - The second step for finding the derivative of fat x is to find the difference f(x + h) − f(x). - f(x + h) f(x) = = (x² x² + 2xh + h² - ])- = 2x + h² - 5h ])x-5h) - (x² - 5x) = ]) (2x + h - 5) Macbook Proarrow_forwardEvaluate the integral using integration by parts. Sx² cos (9x) dxarrow_forwardLet f be defined as follows. y = f(x) = x² - 5x (a) Find the average rate of change of y with respect to x in the following intervals. from x = 4 to x = 5 from x = 4 to x = 4.5 from x = 4 to x = 4.1 (b) Find the (instantaneous) rate of change of y at x = 4. Need Help? Read It Master Itarrow_forward
- Determine whether the inverse of f(x)=x^4+2 is a function. Then, find the inverse.arrow_forwardVelocity of a Ball Thrown into the Air The position function of an object moving along a straight line is given by s = f(t). The average velocity of the object over the time interval [a, b] is the average rate of change of f over [a, b]; its (instantaneous) velocity at t = a is the rate of change of f at a. A ball is thrown straight up with an initial velocity of 128 ft/sec, so that its height (in feet) after t sec is given by s = f(t) = 128t - 16t². (a) What is the average velocity of the ball over the following time intervals? [3,4] [3, 3.5] [3, 3.1] ft/sec ft/sec ft/sec (b) What is the instantaneous velocity at time t = 3? ft/sec (c) What is the instantaneous velocity at time t = 7? ft/sec Is the ball rising or falling at this time? O rising falling (d) When will the ball hit the ground? t = sec Need Help? Read It Watch Itarrow_forwardpractice problem please help!arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY