Chapter 6, Problem 6.36P

Interpretation Introduction

(a)

Interpretation:

Value of Yield strength at $0.2\%$ offset should be determined.

Concept introduction:

Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is defined as the ratio of load per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{P}{\text{A}}$

Where,

P is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

Offset is defined as the yield point in stress strain curve. The figure represents the Stress-Strain curve,

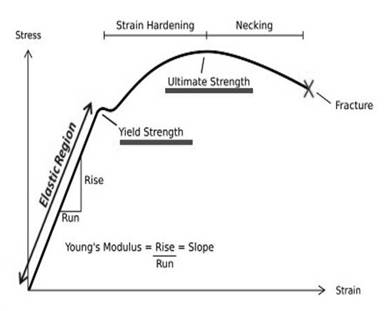
Answer to Problem 6.36P

The requiredvalue of Yield strength at $0.2\%$ offset is $\text{9000}\text{Psi}$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

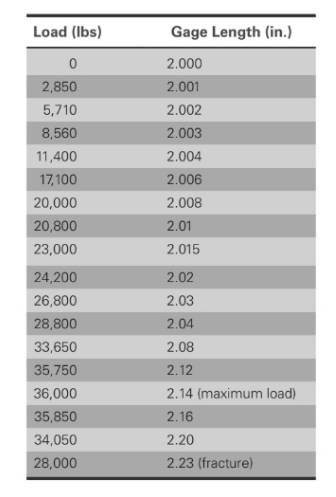
Based on given information

Applying formula of elastic modulus,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is calculated on the basis on force and area. The given formula is,

  $\sigma =\frac{\text{F}}{\text{A}}$

Calculation of stress and strain values are done using spreadsheet shown below,

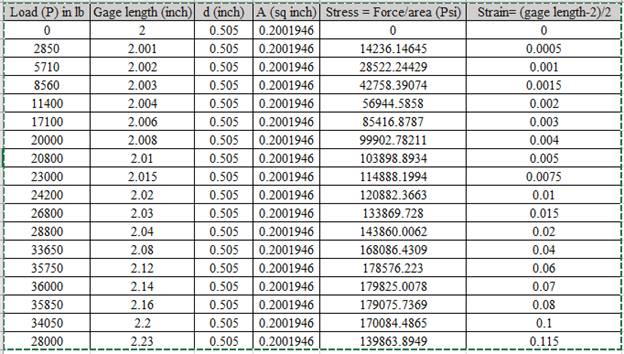
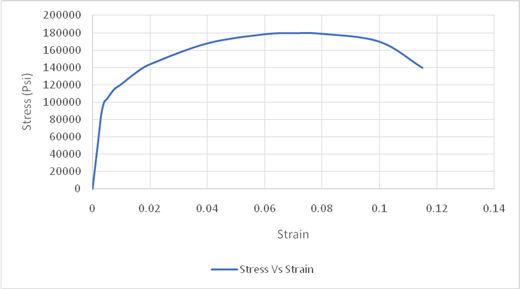
Using the data for Stress-Strain, Drawing the Stress Strain curve,

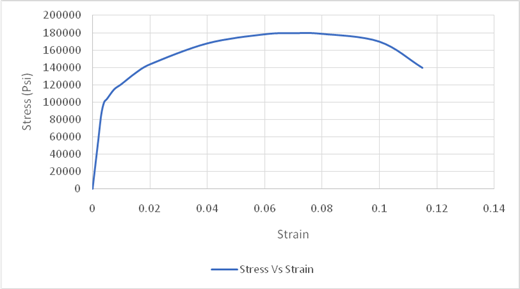
As, the value of offset is given in percentage so converting percentage by dividing it with $100$ .Thus, the required value of offset is,

  $\frac{0.2}{100}=0.002$

Drawing the tie line at offset of $0.002$ for obtaining the value of yield strength,

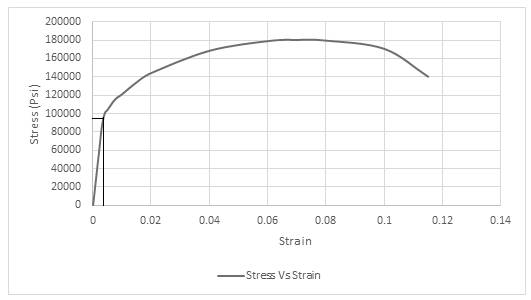
Thus, the required value of yield strength is $\text{9000}\text{Psi}$ at $0.2\%$ offset.

Interpretation Introduction

(b)

Interpretation:

The value of tensile strength for the given condition is to be determined.

Concept introduction:

Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is defined as the ratio of force per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{\text{F}}{\text{A}}$

Where,

F is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

Tensile strength is the maximum load that material can withstand without rapture. The above graph is reflecting relationship between stress and strain.

Answer to Problem 6.36P

Thus, the required value of tensile strength is $\text{180000}\text{Psi}$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

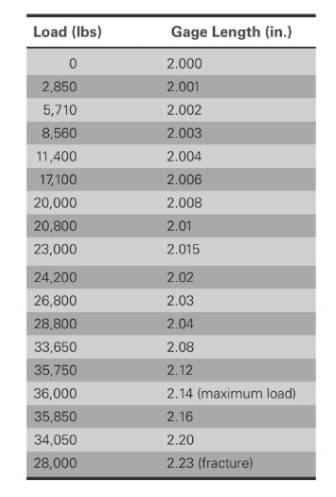
Based on given information

Applying formula of elastic modulus,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is calculated on the basis on force and area. The given formula is,

  $\sigma =\frac{\text{F}}{\text{A}}$

Calculation of stress and strain values are done using spreadsheet shown below,

Using the data for Stress-Strain, Drawing the Stress Strain curve,

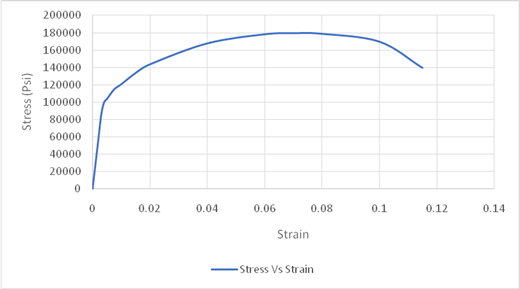
The maximum value of stress is used for obtaining the value of tensile strength. Drawing tie lines as shown in the figure below,

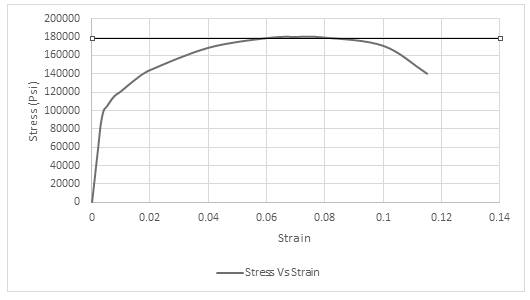
Thus, the required value of tensile strength is $\text{180000}\text{Psi}$.

Interpretation Introduction

(c)

Interpretation:

The value of Modulus of elasticity for the given condition should be calculated.

Concept introduction:

Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is defined as the ratio of force per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{\text{F}}{\text{A}}$

Where,

F is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

The graph of Proportionality constant using modulus of elasticity,

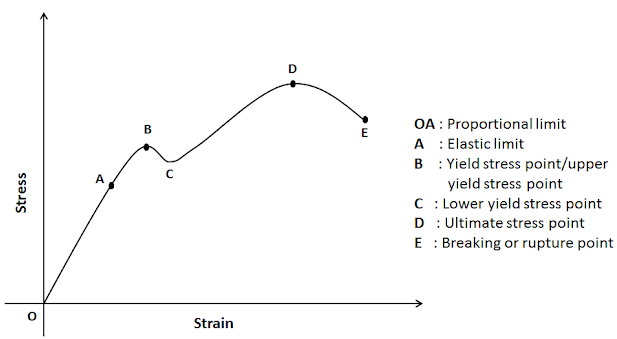
Answer to Problem 6.36P

Thus, the required value of modulus of elasticity is $E=28472292.9\text{Psi}$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

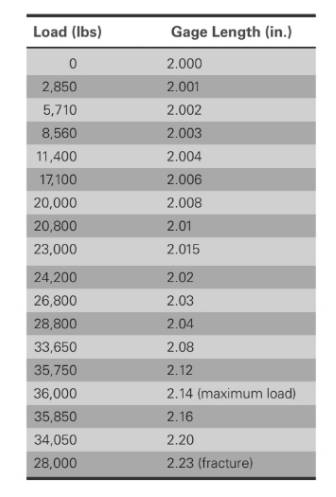
Based on given information

Applying formula of elastic modulus,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is calculated on the basis on force and area. The given formula is,

  $\sigma =\frac{\text{F}}{\text{A}}$

Calculation of stress and strain values are done using spreadsheet shown below,

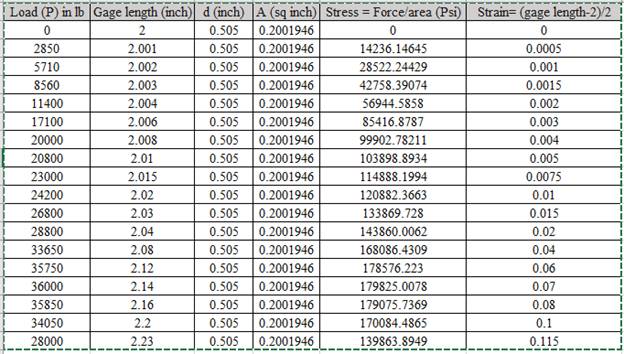
Using the data for Stress-Strain, Drawing the Stress Strain curve,

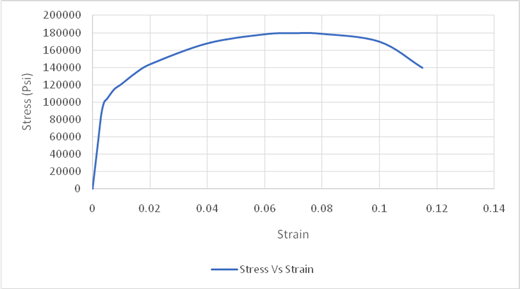
For calculating the modulus of elasticity, the values considered are highlighted in spreadsheet,

Using the above table the value of stress is $\text{56944}\text{.5858}\text{Psi}$ and the value of strain is $\text{0}\text{.002}$.

Calculation of modulus of elasticity,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Putting the values in formula,

  $\begin{array}{l}E=\frac{\text{56944}\text{.5858}}{0.002}\\ E=28472292.9\text{Psi}\end{array}$

Thus, the required value of modulus of elasticity is $E=28472292.9\text{Psi}$.

Interpretation Introduction

(d)

Interpretation:

The value of percentage elongation for the given condition should be calculated.

Concept introduction:

Stress is defined as the ratio of force per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{\text{F}}{\text{A}}$

Where,

F is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

Percentage elongation:

It is defined as the ratio of difference between final length and initial length to initial length. The relationship is given as,

  $\text{\%}\text{Elongation}=\frac{l_f-l_0}{l_0}\times 100$

Where,

  $l_f$ is the length attained after fracture

  $l_0$ is the initial length.

Answer to Problem 6.36P

Thus, the required value of percentage elongation is $10\%$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

Based on the values,

Gage length before fracture is $2\text{inch}$.

Gage length after fracture is $2.20\text{inch}$.

Putting the values in the formula of percentage elongation,

  $\text{\%}\text{Elongation}=\frac{l_f-l_0}{l_0}\times 100$

  $\begin{array}{l}\text{\%}\text{Elongation}=\frac{2.20-2}{2}\times 100\\ \text{\%}\text{Elongation}=10\%\end{array}$

Thus, the required value of percentage elongation is $10\%$.

Interpretation Introduction

(e)

Interpretation:

The value of percentage reduction in area for given condition should be calculated.

Concept introduction:

Stress is defined as the ratio of force per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{\text{F}}{\text{A}}$

Where,

F is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

True Strain: It is defined as the ratio of gage length to instantaneous gage length. The formula is given below:

  $\epsilon \text{=}\text{ln}\left(1-\frac{\Delta l}{l_0}\right)$

Where,

  $\epsilon$ is true strain.

  $\Delta l$ is instantaneous length.

  $l_0$ is gage length.

Percentage Reduction in Area:

It is defined as the ratio of difference between final length and initial length to initial length. The relationship is given as,

  $\text{\%}\text{Area}\text{Reduction}\text{=}\frac{A_0-A_f}{A_0}\times 100$

Where,

  $A_f$ is the final area.

  $A_0$ is the initial area.

Answer to Problem 6.36P

The required value of percentage reduction in area is $\text{\%}\text{Area}\text{Reduction}\text{=}58.58\%$

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

Based on the given values,

Calculation of $A_0$ :

  $\begin{array}{l}{A}_0=\frac{\pi }{4}\times d_0^2\\ d_0=0.505\\ A_0=\frac{\pi }{4}\times {\left(0.505\right)}^2\\ A_0=0.200296{\text{inch}}^2\end{array}$

Calculation of $A_f$ ,

  $\begin{array}{l}{A}_f=\frac{\pi }{4}\times d_f^2\\ d_f=0.325\\ A_f=\frac{\pi }{4}\times {\left(0.325\right)}^2\\ A_f=0.08295{\text{inch}}^2\end{array}$

Substituting the values in the formula of percentage reduction of area,

  $\text{\%}\text{Area}\text{Reduction}\text{=}\frac{A_0-A_f}{A_0}\times 100$

  $\begin{array}{l}{A}_f=0.08295{\text{inch}}^2\\ A_0=0.200296{\text{inch}}^2\end{array}$

  $\begin{array}{l}\text{\%}\text{Area}\text{Reduction}\text{=}\frac{0.200296-0.08295}{0.200296}\times 100\\ \text{\%}\text{Area}\text{Reduction}\text{=}0.5858\times 100\\ \text{\%}\text{Area}\text{Reduction}\text{=}58.58\%\end{array}$

The required value of percentage reduction in area is $\text{\%}\text{Area}\text{Reduction}\text{=}58.58\%$

Interpretation Introduction

(f)

Interpretation:

The value of engineering stress at fracture should be determined.

Concept introduction:

Stress is defined as the ratio of force per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{\text{F}}{\text{A}}$

Where,

F is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

Answer to Problem 6.36P

Thus, the required value of Stress at fracture is $\text{1,39,000}\text{Psi}$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

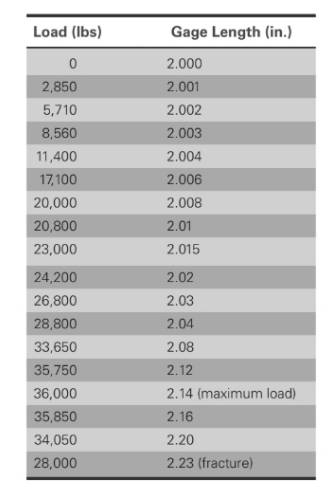
Based on the given values,

Based on given information

Applying formula of elastic modulus,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is calculated on the basis on force and area. The given formula is,

  $\sigma =\frac{\text{F}}{\text{A}}$

Calculation of stress and strain values are done using spreadsheet shown below,

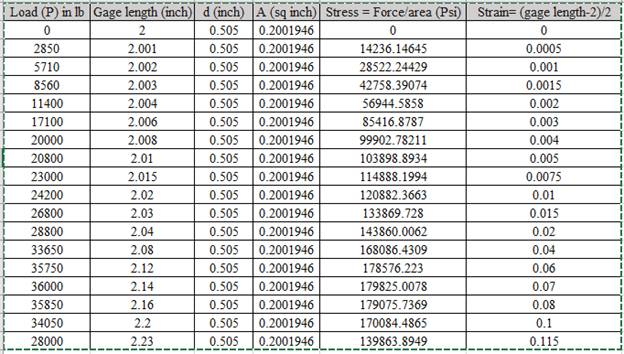
Using the data for Stress-Strain, Drawing the Stress Strain curve,

Drawing the tie lie at the fracture point of Stress-Strain curve,

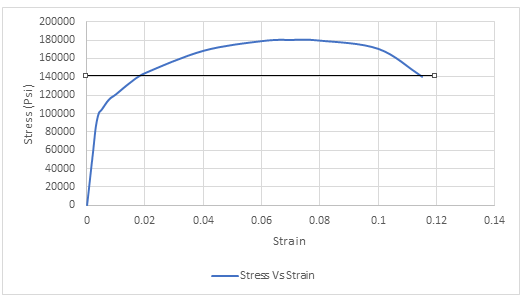
Thus, the required value of Stress at fracture is $\text{1,39,000}\text{Psi}$.

Interpretation Introduction

(g)

Interpretation:

The value of true stress at necking should be calculated.

Concept introduction:

Stress is defined as the ratio of force per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{\text{F}}{\text{A}}$

Where,

F is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

True stress is defined as the ratio of force per unit area. The relationship is given as,

  $\sigma =\frac{F}{A_0}\left(1+\epsilon \right)$

Where,

  $\sigma$ is stress in Psi.

  $F$ is the force.

  $A_0$ is the cross sectional Area

  $\epsilon$ is the strain.

Answer to Problem 6.36P

Thus, the required value of true stress at neck point is $\sigma =158165.91\text{psi}$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

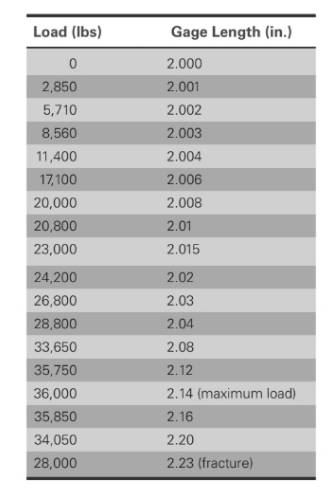
Based on the given values,

The different values of stress, Strain, gage diameter is shown below:

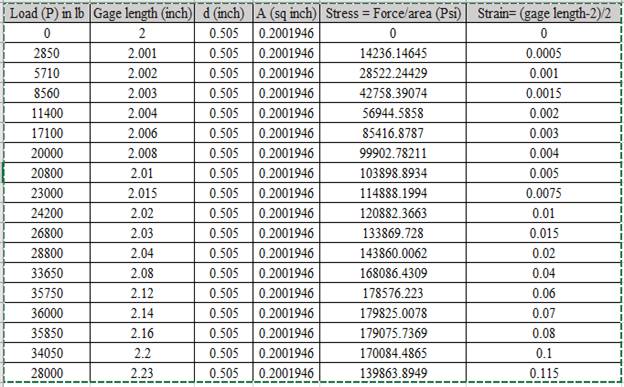
Calculation of true stress:

  $\sigma =\frac{F}{A_0}\left(1+\epsilon \right)$

Following points are considered for calculating the values of true stress at gage length of $2.04$ inch.

  $\begin{array}{l}P=28800lb\\ d_0=\left(0.505\right)\text{inch}\end{array}$

Calculation of area,

  $\begin{array}{l}{A}_0=\frac{\pi }{4}\times d_0^2\\ A_0=\frac{\pi }{4}\times {\left(0.505\right)}^2\\ A_0=0.200296{\text{inch}}^{\text{2}}\end{array}$

Calculation of strain,

  $\epsilon =\frac{l-l_0}{l_0}$

  $\begin{array}{l}\epsilon =\frac{2.20-2}{2}\\ \epsilon =0.1\end{array}$

Putting the values in the formula of true stress,

  $\begin{array}{l}\sigma =\frac{P}{A_0}\left(1+\epsilon \right)\\ \sigma =\frac{28800}{0.200296}\left(1+0.1\right)\\ \sigma =158165.91\text{psi}\end{array}$

Thus, the required value of true stress at neck point is $\sigma =158165.91\text{psi}$.

Interpretation Introduction

(h)

Interpretation:

The value of Modulus of resilience for the given condition should be calculated.

Concept introduction:

Stress is defined as the ratio of force per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{\text{F}}{\text{A}}$

Where,

F is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

Modulus of Resilience is defined as the maximum amount of energy that a material can withstand without creating the permanent distortion of the material.

The relationship of Modulus of Resilience is,

  $\text{Modulus}\text{of}\text{Resilence}=\frac{1}{2}\times {\sigma }_{yield}\times {\epsilon }_{yield}$

Where,

  ${\sigma }_{yield}$ is the value of yield stress.

  ${\epsilon }_{yield}$ is the value of yield strain.

The graph is showing the values of yield stress and strain corresponding to the yield value,

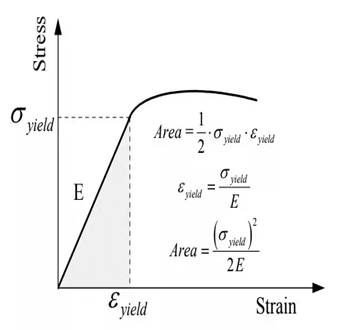
Answer to Problem 6.36P

Thus, the required value of modulus of resilience is $165\text{psi}$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

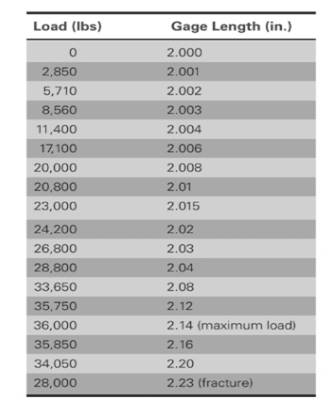
Based on the given values,

The different values of stress, Strain, gage diameter is shown below:

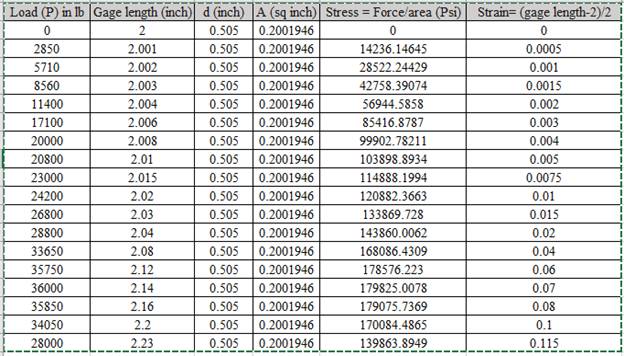
Based on the calculated values of stress and strain. The graph is shown below,

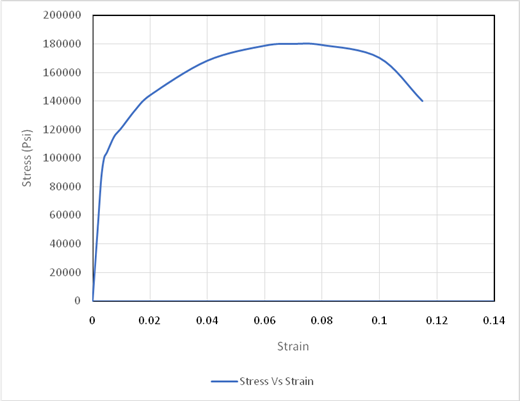
Using the above graph drawing tie lines,

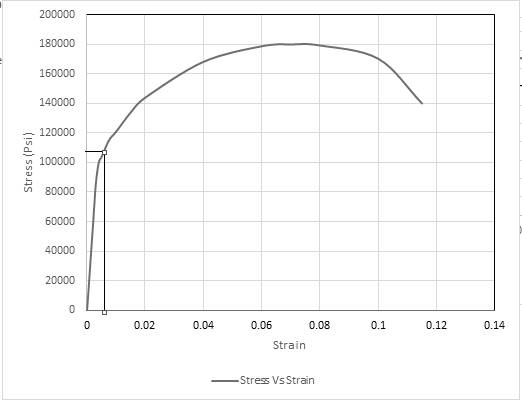
Thus, based on the tie line, The value for yield stress is $110000\text{psi}$ and the value of yield strain is $\text{0}\text{.003}$.

Substituting the values for calculating the modulus of resilience,

  $\begin{array}{l}\text{Modulus}\text{of}\text{Resilence}=\frac{1}{2}\times {\sigma }_{yield}\times {\epsilon }_{yield}\\ \text{Modulus}\text{of}\text{Resilence}=\frac{1}{2}\times 110000\times 0.003\\ \text{Modulus}\text{of}\text{Resilence}=165\text{psi}\end{array}$

Thus, the required value of modulus of resilience is $165\text{psi}$.

Interpretation Introduction

(i)

Interpretation:

The value of elastic and plastic strain corresponding to fracture should be determined.

Concept introduction:

Elastic strainis defined as the distortion in the structure.

Plastic Strain is defined as the permanent distortion of structure.

The graph for elastic and plastic strain is shown below:

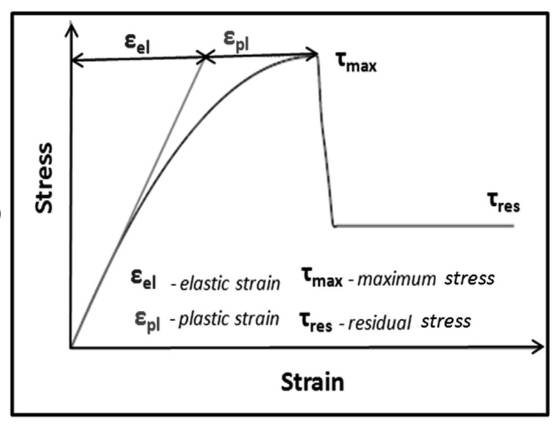
Answer to Problem 6.36P

Thus, the required value of elastic strain is $2\times {10}^{-3}$.

Thus, the required value of plastic strain is $\text{0}\text{.11}$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

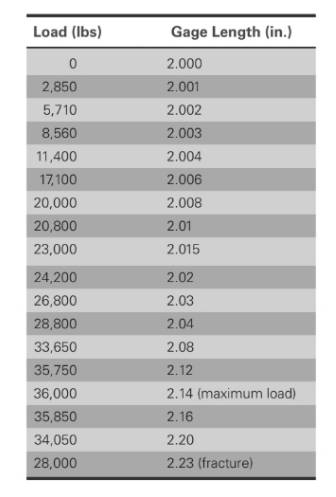
Based on the given values,

The different values of stress, Strain, gage diameter is shown below:

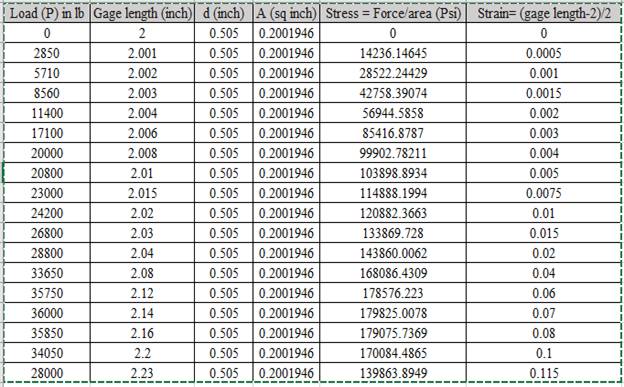
Based on the given values.

Plotting the graph,

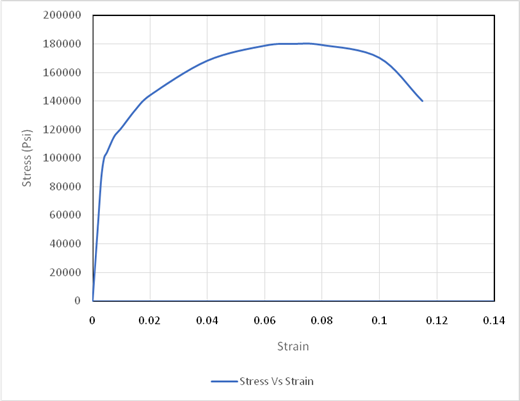
Based on given information

Applying formula of elastic modulus,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is calculated on the basis on force and area. The given formula is,

  $\sigma =\frac{\text{F}}{\text{A}}$

For calculating the modulus of elasticity, the values considered are highlighted in spreadsheet,

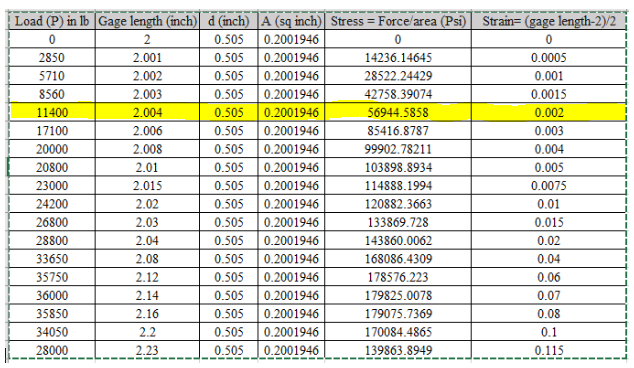
Using the above table the value of stress is $\text{56944}\text{.5858}\text{Psi}$ and the value of modulus of elasticity is calculated using part (c )

  $E=28472292.9\text{Psi}$

Putting the value of modulus of elasticity and stress,

Calculation of elastic strain,

  $\text{Strain}=\frac{\text{Stress}}{\text{E}}$

Putting the values in formula,

  $\begin{array}{l}\text{Strain}=\frac{56944.5858}{28472292.9}\\ \text{Strain}=2\times {10}^{-3}\end{array}$

Thus, the required value of elastic strain is $2\times {10}^{-3}$.

Using graph, drawing tie lines for determining the value of plastic strain,

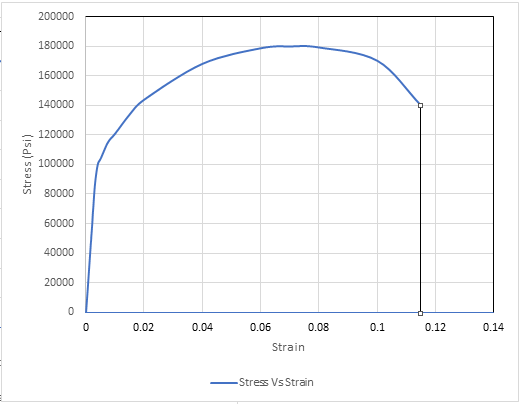
Thus, the required value of plastic strain is $\text{0}\text{.11}$.

Interpretation Introduction

(j)

Interpretation:

The transverse and axial strain for given condition should be determined. Also, the value of Poisson's ratio is to be calculated.

Concept introduction:

Transverse Strain is defined as the ratio of change in diameter to original diameter. The relationship is given as,

  ${\epsilon }_{Transverse}=\frac{\text{Δd}}{\text{d}}$

Where,

  $\text{Δd}$ is change in diameter.

d is the original diameter.

Axial Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

Poisson's Ratio:

It is defined as the ratio of transverse strain to axial strain represented as:

  $v=-\left(\frac{{\epsilon }_{Transverse}}{{\epsilon }_{Axial}}\right)$

Answer to Problem 6.36P

The required value of transverse strain is ${\epsilon }_{Transverse}=-1.98\times {10}^{-3}$.

Thus, the required value of axial strain is ${\epsilon }_{Axial}=2$.

The required value of Poisson's ratio is $v=9.9\times {10}^{-4}$.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

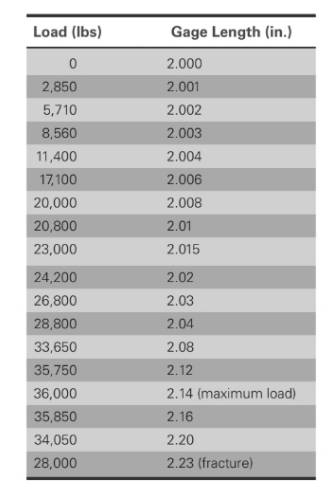
Load for sample is $11400\text{lbs}$.

Diameter of sample is $0.504\text{inch}$.

Based on the given values,

The different values of stress, Strain, gage diameter is shown below:

Calculation of transverse strain,

  ${\epsilon }_{Transverse}=\frac{\text{Δd}}{\text{d}}$

Where,

  $\begin{array}{l}{\epsilon }_{Transverse}=\frac{\text{Δd}}{\text{d}}\\ \text{Δd}=0.504-0.505\\ \text{Δd}=1\times {10}^{-3}\\ \text{d}=0.505\end{array}$

Putting the values,

  $\begin{array}{l}{\epsilon }_{Transverse}=\frac{1\times {10}^{-3}}{0.505}\\ {\epsilon }_{Transverse}=-1.98\times {10}^{-3}\end{array}$

The required value of transverse strain is ${\epsilon }_{Transverse}=-1.98\times {10}^{-3}$.

Calculation of axial strain,

  $\epsilon =\frac{l}{l_0}$

Where,

  $\begin{array}{l}l=2.004-2\\ l=4\times {10}^{-3}\\ l_0=2\times {10}^{-3}\\ {\epsilon }_{Axial}=\frac{4\times {10}^{-3}}{2\times {10}^{-3}}\\ {\epsilon }_{Axial}=2\end{array}$

Thus, the required value of axial strain is ${\epsilon }_{Axial}=2$.

Calculation of Poisson's ratio,

  $v=-\left(\frac{{\epsilon }_{Transverse}}{{\epsilon }_{Axial}}\right)$

Putting the value of transverse and axial strain,

  $\begin{array}{l}v=-\left(\frac{-1.98\times {10}^{-3}}{2}\right)\\ v=9.9\times {10}^{-4}\end{array}$

Thus, the required value of Poisson's ratio is $v=9.9\times {10}^{-4}$.

Interpretation Introduction

(k)

Interpretation:

The value of tensile strength for 416 stainless steel is to be determined. Also, the comparison of values for tensile strength should be explained.

Concept introduction:

Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is defined as the ratio of force per unit area. It is denoted by $\sigma$.

  $\sigma =\frac{\text{F}}{\text{A}}$

Where,

F is the force in newton.

A is area in square meter.

Strain is defined as the ratio of change in length to original length. It is denoted by $\epsilon$.

  $\epsilon =\frac{l}{l_0}$

Where,

  $l$ is the length in meter.

  $l_0$ is the original length in meter.

Strain is dimensionless quantity.

Tensile strength is the maximum load that material can withstand without rapture. The above graph is reflecting relationship between stress and strain.

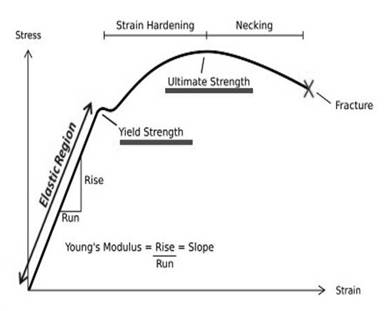
Answer to Problem 6.36P

Thus, the required calculated value of tensile strength is $\text{180000}\text{Psi}$.

Thus, the value of tensile strength remains the same after quenching and tempering.

Explanation of Solution

Given information:

The data for AISI-SAE stainless steel is given below:

Diameter of stainless steel is $0.505\text{inch}$.

Gage length before fracture is $2\text{inch}$.

After fracture, the given values are,

Gage length after fracture is $2.20\text{inch}$.

Diameter of stainless steel is $0.325\text{inch}$.

The values of load correspond to gage length is shown in table,

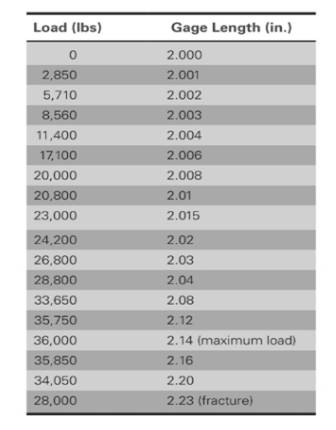
Load for sample is $11400\text{lbs}$.

Diameter of sample is $0.504\text{inch}$.

Based on given information

Applying formula of elastic modulus,

  $\text{E}=\frac{\text{Stress}}{\text{Strain}}$

Stress is calculated on the basis on force and area. The given formula is,

  $\sigma =\frac{\text{F}}{\text{A}}$

Calculation of stress and strain values are done using spreadsheet shown below,

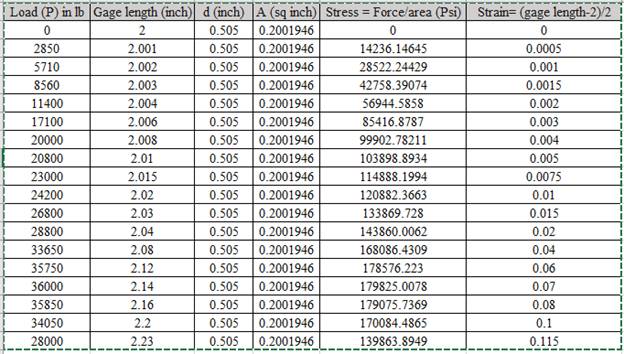
Using the data for Stress-Strain, Drawing the Stress Strain curve,

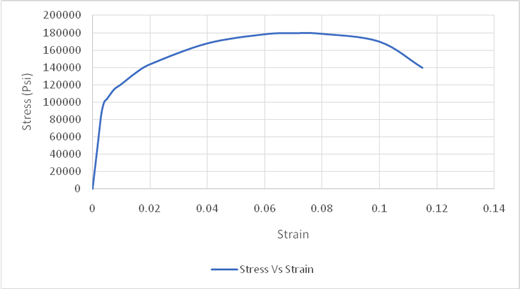
The maximum value of stress is used for obtaining the value of tensile strength. Drawing tie lines as shown in the figure below,

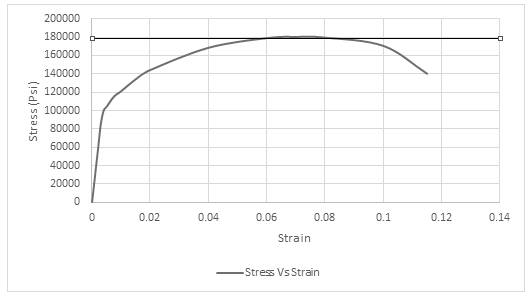
Thus, the required value of tensile strength is $\text{180000}\text{Psi}$.

Based on the given information the physical and mechanical properties of 416 stainless steel is shown below:

Thus, the required calculated value of tensile strength is $\text{180000}\text{Psi}$.

Thus, the required calculated value of yield strength is $\text{1,10,000}\text{Psi}$.

The values of 416 stainless steel when quenched and tempered is shown in table,

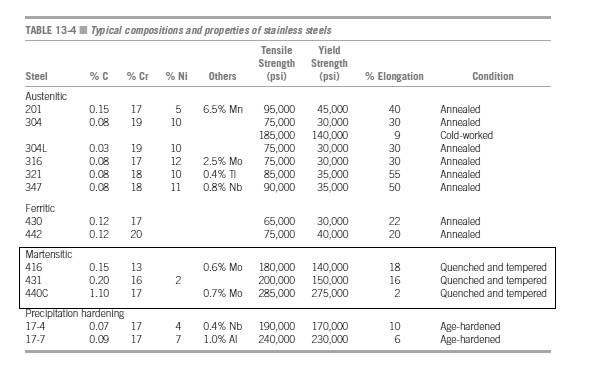
Thus, the value of tensile strength remains the same after quenching and tempering.