
MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
9th Edition
ISBN: 9780136415893
Author: Tannenbaum
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 6, Problem 36E
A space mission is scheduled to visit the moons Callisto (C), Ganymede (G), lo Mimas (M), and Titan (T) to collect rock samples at each and then return to Earth (E). The travel times (in years) are given in the weighted graph shown in Fig. 6-44. (Note: This is the interplanetary TSP discussed in Example 6.11.)
a. Find the nearest-neighbor tour with starting vertex E. Give the total travel time of this tour.
b. Find the nearest-neighbor tour with starting vertex T Write the tour as it would be traveled by an expedition starting and ending at E. Give the total travel time of this tour.
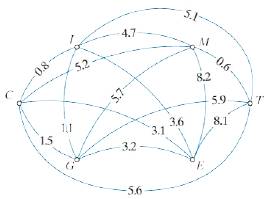
Figure 6-44
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
No chatgpt pls will upvote
Already got wrong chatgpt answer
.
In a town with 5000 adults, a sample of 50 is selected using SRSWOR and asked their opinion of a proposed municipal project; 30 are found to favor it and 20 oppose it. If, in fact, the adults of the town were equally divided on the proposal, what would be the probability of observing what has been observed? Approximate using the Binomial distribution. Compare this with the exact probability which is 0.0418.
1.2.19. Let and s be natural numbers. Let G be the simple graph with vertex set
Vo... V„−1 such that v; ↔ v; if and only if |ji| Є (r,s). Prove that S has exactly k
components, where k is the greatest common divisor of {n, r,s}.
Chapter 6 Solutions
MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
Ch. 6 - For the graph shown in Fig. 6-19, a.find three...Ch. 6 - For the graph shown in Fig. 6-20, a.find three...Ch. 6 - Find all possible Hamilton circuits in the graph...Ch. 6 - Find all possible Hamilton circuits in the graph...Ch. 6 - For the graph shown in Fig.6-23, a. find a...Ch. 6 - For the graph shown in Fig.6-24, a. find a...Ch. 6 - Suppose D,G,E,A,H,C,B,F,D is a Hamilton circuit in...Ch. 6 - Suppose G,B,D,C,A,F,E,G is a Hamilton circuit in a...Ch. 6 - Consider the graph in Fig. 6-25. a. Find the five...Ch. 6 - Consider the graph in Fig.6-26. a. Find all the...
Ch. 6 - Consider the graph in Fig.6-27. a. Find all the...Ch. 6 - Prob. 12ECh. 6 - For the graph in Fig.6-29 a. find a Hamilton path...Ch. 6 - For the graph in Fig.6-30 a. find a Hamilton path...Ch. 6 - Explain why the graph shown in Fig.6-31 has...Ch. 6 - Explain why the graph shown in Fig.6-32 has...Ch. 6 - For the weighted shown in Fig 6-33, a.find the...Ch. 6 - For the weighted graph shown in Fig6-34, a.find...Ch. 6 - For the weighted graph shown in Fig6-35, a.find a...Ch. 6 - For the weighted graph shown in Fig6-36, a.find a...Ch. 6 - Suppose you have a supercomputer that can generate...Ch. 6 - Suppose you have a supercomputer that can generate...Ch. 6 - Prob. 23ECh. 6 - a. How many edges are there in K200? b. How many...Ch. 6 - In each case, find the value of N. a. KN has 120...Ch. 6 - In each case, find the value of N. a. KN has 720...Ch. 6 - Find an optimal tour for the TSP given in...Ch. 6 - Find an optimal tour for the TSP given in...Ch. 6 - A truck must deliver furniture to stores located...Ch. 6 - A social worker starts from her home A, must visit...Ch. 6 - You are planning to visit four cities A, B, C, and...Ch. 6 - An unmanned rover must be routed to visit four...Ch. 6 - For the weighted graph shown in Fig.6-41, i find...Ch. 6 - A delivery service must deliver packages at...Ch. 6 - Prob. 35ECh. 6 - A space mission is scheduled to visit the moons...Ch. 6 - This exercise refers to the furniture truck TSP...Ch. 6 - This exercise refers to the social worker TSP...Ch. 6 - Darren is a sales rep whose territory consists of...Ch. 6 - The Platonic Cowboys are a country and western...Ch. 6 - Find the repetitive nearest-neighbor tour and give...Ch. 6 - Prob. 42ECh. 6 - This exercise is a continuation of Darrens sales...Ch. 6 - This exercise is a continuation of the Platonic...Ch. 6 - Prob. 45ECh. 6 - Prob. 46ECh. 6 - Find the cheapest-link tour and give its cost for...Ch. 6 - Find the cheapest-link tour for the social worker...Ch. 6 - For the Brute-Force Bandits concert tour discussed...Ch. 6 - For the weighted graph shown in Fig.6-47, find the...Ch. 6 - For Darrens sales trip problem discussed in...Ch. 6 - For the Platonic Cowboys concert tour discussed in...Ch. 6 - A rover on the planet Mercuria has to visit six...Ch. 6 - A robotic laser must drill holes on five sites A,...Ch. 6 - Prob. 55ECh. 6 - Prob. 56ECh. 6 - Suppose that in solving a TSP you find an...Ch. 6 - Prob. 58ECh. 6 - Prob. 59ECh. 6 - Prob. 60ECh. 6 - Prob. 61ECh. 6 - If the number of edges in K500 is x and the number...Ch. 6 - Explain why the cheapest edge in any graph is...Ch. 6 - a. Explain why the graph that has a bridge cannot...Ch. 6 - Julie is the marketing manager for a small...Ch. 6 - 66. m by n grid graphs. An m by n grid graph...Ch. 6 - Complete bipartite graphs. A complete bipartite...Ch. 6 - Prob. 68ECh. 6 - Diracs theorem. If G is a connected graph with N...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Question 3 over a field K. In this question, MË(K) denotes the set of n × n matrices (a) Suppose that A Є Mn(K) is an invertible matrix. Is it always true that A is equivalent to A-¹? Justify your answer. (b) Let B be given by 8 B = 0 7 7 0 -7 7 Working over the field F2 with 2 elements, compute the rank of B as an element of M2(F2). (c) Let 1 C -1 1 [4] [6] and consider C as an element of M3(Q). Determine the minimal polynomial mc(x) and hence, or otherwise, show that C can not be diagonalised. [7] (d) Show that C in (c) considered as an element of M3(R) can be diagonalised. Write down all the eigenvalues. Show your working. [8]arrow_forward16. Solve the given differential equation: y" + 4y sin (t)u(t 2π), - y(0) = 1, y'(0) = 0 Given, 1 (x² + 1)(x²+4) 1/3 -1/3 = + x²+1 x² +4 Send your answer in pen and paper don't r eputed ur self down Don't send the same previous answer that was Al generated Don't use any Al tool show ur answer in pe n and paper then takearrow_forwardR denotes the field of real numbers, Q denotes the field of rationals, and Fp denotes the field of p elements given by integers modulo p. You may refer to general results from lectures. Question 1 For each non-negative integer m, let R[x]m denote the vector space consisting of the polynomials in x with coefficients in R and of degree ≤ m. x²+2, V3 = 5. Prove that (V1, V2, V3) is a linearly independent (a) Let vi = x, V2 = list in R[x] 3. (b) Let V1, V2, V3 be as defined in (a). Find a vector v € R[×]3 such that (V1, V2, V3, V4) is a basis of R[x] 3. [8] [6] (c) Prove that the map ƒ from R[x] 2 to R[x]3 given by f(p(x)) = xp(x) — xp(0) is a linear map. [6] (d) Write down the matrix for the map ƒ defined in (c) with respect to the basis (2,2x + 1, x²) of R[x] 2 and the basis (1, x, x², x³) of R[x] 3. [5]arrow_forward
- Question 4 (a) The following matrices represent linear maps on R² with respect to an orthonormal basis: = [1/√5 2/√5 [2/√5 -1/√5] " [1/√5 2/√5] A = B = [2/√5 1/√5] 1 C = D = = = [ 1/3/5 2/35] 1/√5 2/√5 -2/√5 1/√5' For each of the matrices A, B, C, D, state whether it represents a self-adjoint linear map, an orthogonal linear map, both, or neither. (b) For the quadratic form q(x, y, z) = y² + 2xy +2yz over R, write down a linear change of variables to u, v, w such that q in these terms is in canonical form for Sylvester's Law of Inertia. [6] [4]arrow_forwardpart b pleasearrow_forwardQuestion 5 (a) Let a, b, c, d, e, ƒ Є K where K is a field. Suppose that the determinant of the matrix a cl |df equals 3 and the determinant of determinant of the matrix a+3b cl d+3e f ГЪ e [ c ] equals 2. Compute the [5] (b) Calculate the adjugate Adj (A) of the 2 × 2 matrix [1 2 A = over R. (c) Working over the field F3 with 3 elements, use row and column operations to put the matrix [6] 0123] A = 3210 into canonical form for equivalence and write down the canonical form. What is the rank of A as a matrix over F3? 4arrow_forward
- Question 2 In this question, V = Q4 and - U = {(x, y, z, w) EV | x+y2w+ z = 0}, W = {(x, y, z, w) € V | x − 2y + w − z = 0}, Z = {(x, y, z, w) € V | xyzw = 0}. (a) Determine which of U, W, Z are subspaces of V. Justify your answers. (b) Show that UW is a subspace of V and determine its dimension. (c) Is VU+W? Is V = UW? Justify your answers. [10] [7] '00'arrow_forwardGood explanation it sure experts solve itarrow_forwardBest explains it not need guidelines okkarrow_forward
- Task number: A1.1, A1.7 Topic: Celestial Navigation, Compass - Magnetic and Gyro Activ Determine compass error (magnetic and gyro) using azimuth choosing a suitable celestial body (Sun/ Stars/ Planets/ Moon). Apply variation to find the deviation of the magnetic compass. Minimum number of times that activity should be recorded: 6 (2 each phase) Sample calculation (Azimuth- Planets): On 06th May 2006 at 22h20m 10s UTC, a vessel in position 48°00'N 050°00'E observed Mars bearing 327° by compass. Find the compass error. If variation was 4.0° East, calculate the deviation. GHA Mars (06d 22h): Increment (20m 10s): 089° 55.7' 005° 02.5' v (0.9): (+) 00.3' GHA Mars: 094° 58.5' Longitude (E): (+) 050° 00.0' (plus- since longitude is easterly) LHA Mars: 144° 58.5' Declination (06d 22h): d (0.2): N 024° 18.6' (-) 00.1' Declination Mars: N 024° 18.5' P=144° 58.5' (If LHA<180°, P=LHA) A Tan Latitude/ Tan P A Tan 48° 00' Tan 144° 58.5' A = 1.584646985 N (A is named opposite to latitude, except when…arrow_forwardTask number: A1.1, A1.7 Topic: Celestial Navigation, Compass - Magnetic and Gyro Activ Determine compass error (magnetic and gyro) using azimuth choosing a suitable celestial body (Sun/ Stars/ Planets/ Moon). Apply variation to find the deviation of the magnetic compass. Minimum number of times that activity should be recorded: 6 (2 each phase) Sample calculation (Azimuth- Planets): On 06th May 2006 at 22h20m 10s UTC, a vessel in position 48°00'N 050°00'E observed Mars bearing 327° by compass. Find the compass error. If variation was 4.0° East, calculate the deviation. GHA Mars (06d 22h): Increment (20m 10s): 089° 55.7' 005° 02.5' v (0.9): (+) 00.3' GHA Mars: 094° 58.5' Longitude (E): (+) 050° 00.0' (plus- since longitude is easterly) LHA Mars: 144° 58.5' Declination (06d 22h): d (0.2): N 024° 18.6' (-) 00.1' Declination Mars: N 024° 18.5' P=144° 58.5' (If LHA<180°, P=LHA) A Tan Latitude/ Tan P A Tan 48° 00' Tan 144° 58.5' A = 1.584646985 N (A is named opposite to latitude, except when…arrow_forwardActiv Determine compass error using amplitude (Sun). Minimum number of times that activity should be performed: 3 (1 each phase) Sample calculation (Amplitude- Sun): On 07th May 2006 at Sunset, a vessel in position 10°00'N 010°00'W observed the Sun bearing 288° by compass. Find the compass error. LMT Sunset: LIT: (+) 00d 07d 18h 00h 13m 40m UTC Sunset: 07d 18h 53m (added- since longitude is westerly) Declination (07d 18h): N 016° 55.5' d (0.7): (+) 00.6' Declination Sun: N 016° 56.1' Sin Amplitude = Sin Declination/Cos Latitude = Sin 016°56.1'/ Cos 10°00' = 0.295780189 Amplitude=W17.2N (The prefix of amplitude is named easterly if body is rising, and westerly if body is setting. The suffix is named same as declination) True Bearing=287.2° Compass Bearing= 288.0° Compass Error = 0.8° Westarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, 

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY