MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
9th Edition
ISBN: 9780136415893
Author: Tannenbaum
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6, Problem 37E
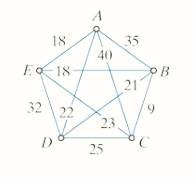
This exercise refers to the furniture truck TSP introduced in Exercise 29 (see Fig. 6-39).
a. Find the nearest-neighbor tour starting at
b. Find the nearest-neighbor tour starting at
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
12:25 AM Sun Dec 22
uestion 6- Week 8: QuX
Assume that a company X +
→ C
ezto.mheducation.com
Week 8: Quiz i
Saved
6
4
points
Help
Save & Exit
Submit
Assume that a company is considering purchasing a machine for $50,000 that will have a five-year useful life and a $5,000 salvage value. The
machine will lower operating costs by $17,000 per year. The company's required rate of return is 15%. The net present value of this investment
is closest to:
Click here to view Exhibit 12B-1 and Exhibit 12B-2, to determine the appropriate discount factor(s) using the tables provided.
00:33:45
Multiple Choice
О
$6,984.
$11,859.
$22,919.
○ $9,469,
Mc
Graw
Hill
2
100-
No chatgpt pls will upvote
7. [10 marks]
Let G
=
(V,E) be a 3-connected graph. We prove that for every x, y, z Є V, there is a
cycle in G on which x, y, and z all lie.
(a) First prove that there are two internally disjoint xy-paths Po and P₁.
(b) If z is on either Po or P₁, then combining Po and P₁ produces a cycle on which
x, y, and z all lie. So assume that z is not on Po and not on P₁. Now prove that
there are three paths Qo, Q1, and Q2 such that:
⚫each Qi starts at z;
• each Qi ends at a vertex w; that is on Po or on P₁, where wo, w₁, and w₂ are
distinct;
the paths Qo, Q1, Q2 are disjoint from each other (except at the start vertex
2) and are disjoint from the paths Po and P₁ (except at the end vertices wo,
W1, and w₂).
(c) Use paths Po, P₁, Qo, Q1, and Q2 to prove that there is a cycle on which x, y, and
z all lie. (To do this, notice that two of the w; must be on the same Pj.)
Chapter 6 Solutions
MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
Ch. 6 - For the graph shown in Fig. 6-19, a.find three...Ch. 6 - For the graph shown in Fig. 6-20, a.find three...Ch. 6 - Find all possible Hamilton circuits in the graph...Ch. 6 - Find all possible Hamilton circuits in the graph...Ch. 6 - For the graph shown in Fig.6-23, a. find a...Ch. 6 - For the graph shown in Fig.6-24, a. find a...Ch. 6 - Suppose D,G,E,A,H,C,B,F,D is a Hamilton circuit in...Ch. 6 - Suppose G,B,D,C,A,F,E,G is a Hamilton circuit in a...Ch. 6 - Consider the graph in Fig. 6-25. a. Find the five...Ch. 6 - Consider the graph in Fig.6-26. a. Find all the...
Ch. 6 - Consider the graph in Fig.6-27. a. Find all the...Ch. 6 - Prob. 12ECh. 6 - For the graph in Fig.6-29 a. find a Hamilton path...Ch. 6 - For the graph in Fig.6-30 a. find a Hamilton path...Ch. 6 - Explain why the graph shown in Fig.6-31 has...Ch. 6 - Explain why the graph shown in Fig.6-32 has...Ch. 6 - For the weighted shown in Fig 6-33, a.find the...Ch. 6 - For the weighted graph shown in Fig6-34, a.find...Ch. 6 - For the weighted graph shown in Fig6-35, a.find a...Ch. 6 - For the weighted graph shown in Fig6-36, a.find a...Ch. 6 - Suppose you have a supercomputer that can generate...Ch. 6 - Suppose you have a supercomputer that can generate...Ch. 6 - Prob. 23ECh. 6 - a. How many edges are there in K200? b. How many...Ch. 6 - In each case, find the value of N. a. KN has 120...Ch. 6 - In each case, find the value of N. a. KN has 720...Ch. 6 - Find an optimal tour for the TSP given in...Ch. 6 - Find an optimal tour for the TSP given in...Ch. 6 - A truck must deliver furniture to stores located...Ch. 6 - A social worker starts from her home A, must visit...Ch. 6 - You are planning to visit four cities A, B, C, and...Ch. 6 - An unmanned rover must be routed to visit four...Ch. 6 - For the weighted graph shown in Fig.6-41, i find...Ch. 6 - A delivery service must deliver packages at...Ch. 6 - Prob. 35ECh. 6 - A space mission is scheduled to visit the moons...Ch. 6 - This exercise refers to the furniture truck TSP...Ch. 6 - This exercise refers to the social worker TSP...Ch. 6 - Darren is a sales rep whose territory consists of...Ch. 6 - The Platonic Cowboys are a country and western...Ch. 6 - Find the repetitive nearest-neighbor tour and give...Ch. 6 - Prob. 42ECh. 6 - This exercise is a continuation of Darrens sales...Ch. 6 - This exercise is a continuation of the Platonic...Ch. 6 - Prob. 45ECh. 6 - Prob. 46ECh. 6 - Find the cheapest-link tour and give its cost for...Ch. 6 - Find the cheapest-link tour for the social worker...Ch. 6 - For the Brute-Force Bandits concert tour discussed...Ch. 6 - For the weighted graph shown in Fig.6-47, find the...Ch. 6 - For Darrens sales trip problem discussed in...Ch. 6 - For the Platonic Cowboys concert tour discussed in...Ch. 6 - A rover on the planet Mercuria has to visit six...Ch. 6 - A robotic laser must drill holes on five sites A,...Ch. 6 - Prob. 55ECh. 6 - Prob. 56ECh. 6 - Suppose that in solving a TSP you find an...Ch. 6 - Prob. 58ECh. 6 - Prob. 59ECh. 6 - Prob. 60ECh. 6 - Prob. 61ECh. 6 - If the number of edges in K500 is x and the number...Ch. 6 - Explain why the cheapest edge in any graph is...Ch. 6 - a. Explain why the graph that has a bridge cannot...Ch. 6 - Julie is the marketing manager for a small...Ch. 6 - 66. m by n grid graphs. An m by n grid graph...Ch. 6 - Complete bipartite graphs. A complete bipartite...Ch. 6 - Prob. 68ECh. 6 - Diracs theorem. If G is a connected graph with N...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 6. [10 marks] Let T be a tree with n ≥ 2 vertices and leaves. Let BL(T) denote the block graph of T. (a) How many vertices does BL(T) have? (b) How many edges does BL(T) have? Prove that your answers are correct.arrow_forward4. [10 marks] Find both a matching of maximum size and a vertex cover of minimum size in the following bipartite graph. Prove that your answer is correct. ย ພarrow_forward5. [10 marks] Let G = (V,E) be a graph, and let X C V be a set of vertices. Prove that if |S||N(S)\X for every SCX, then G contains a matching M that matches every vertex of X (i.e., such that every x X is an end of an edge in M).arrow_forward
- Q/show that 2" +4 has a removable discontinuity at Z=2i Z(≥2-21)arrow_forwardRefer to page 100 for problems on graph theory and linear algebra. Instructions: • Analyze the adjacency matrix of a given graph to find its eigenvalues and eigenvectors. • Interpret the eigenvalues in the context of graph properties like connectivity or clustering. Discuss applications of spectral graph theory in network analysis. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 110 for problems on optimization. Instructions: Given a loss function, analyze its critical points to identify minima and maxima. • Discuss the role of gradient descent in finding the optimal solution. . Compare convex and non-convex functions and their implications for optimization. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 140 for problems on infinite sets. Instructions: • Compare the cardinalities of given sets and classify them as finite, countable, or uncountable. • Prove or disprove the equivalence of two sets using bijections. • Discuss the implications of Cantor's theorem on real-world computation. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 120 for problems on numerical computation. Instructions: • Analyze the sources of error in a given numerical method (e.g., round-off, truncation). • Compute the error bounds for approximating the solution of an equation. • Discuss strategies to minimize error in iterative methods like Newton-Raphson. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 145 for problems on constrained optimization. Instructions: • Solve an optimization problem with constraints using the method of Lagrange multipliers. • • Interpret the significance of the Lagrange multipliers in the given context. Discuss the applications of this method in machine learning or operations research. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Only 100% sure experts solve it correct complete solutions okarrow_forwardGive an example of a graph with at least 3 vertices that has exactly 2 automorphisms(one of which is necessarily the identity automorphism). Prove that your example iscorrect.arrow_forward3. [10 marks] Let Go (Vo, Eo) and G₁ = (V1, E1) be two graphs that ⚫ have at least 2 vertices each, ⚫are disjoint (i.e., Von V₁ = 0), ⚫ and are both Eulerian. Consider connecting Go and G₁ by adding a set of new edges F, where each new edge has one end in Vo and the other end in V₁. (a) Is it possible to add a set of edges F of the form (x, y) with x € Vo and y = V₁ so that the resulting graph (VUV₁, Eo UE₁ UF) is Eulerian? (b) If so, what is the size of the smallest possible F? Prove that your answers are correct.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License