MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
9th Edition
ISBN: 9780136415893
Author: Tannenbaum
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
thumb_up100%
Chapter 1, Problem 1E
Figure 1-8 shows the preference ballots for an election with 21 voters and 5 candidates. Write out the preference schedule for this election.
Figure 1-8
Expert Solution & Answer
To determine
To find:
The preference schedule for the election with given preference ballots.
Answer to Problem 1E
Solution:
The preference schedule for the preference ballots for 21 voters and 5 candidates is,
| Number of Voters | 5 | 5 | 3 | 3 | 3 | 2 |
| 1st Choice | A | C | A | B | D | D |
| 2nd Choice | B | E | D | E | C | C |
| 3rd Choice | C | D | B | A | B | B |
| 4th Choice | D | A | C | C | E | A |
| 5th Choice | E | B | E | D | A | E |
Explanation of Solution
Given:
The preference ballots for 21 voters and 5 candidates are given as,
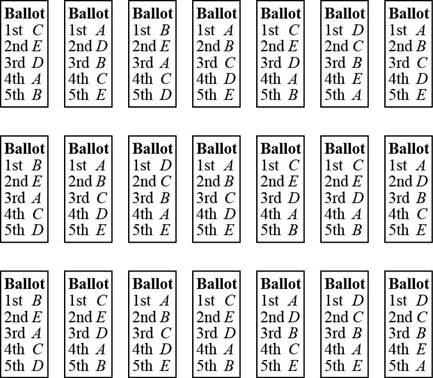
Calculation:
The ballots of the same preferences are grouped together as,
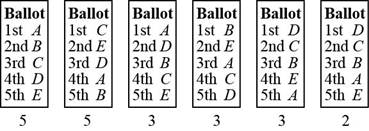
The preference schedule table for the above ballots is given by,
| Number of Voters | 5 | 5 | 3 | 3 | 3 | 2 |
| 1st Choice | A | C | A | B | D | D |
| 2nd Choice | B | E | D | E | C | C |
| 3rd Choice | C | D | B | A | B | B |
| 4th Choice | D | A | C | C | E | A |
| 5th Choice | E | B | E | D | A | E |
Conclusion:
The preference schedule for the preference ballots for 21 voters and 5 candidates is,
| Number of Voters | 5 | 5 | 3 | 3 | 3 | 2 |
| 1st Choice | A | C | A | B | D | D |
| 2nd Choice | B | E | D | E | C | C |
| 3rd Choice | C | D | B | A | B | B |
| 4th Choice | D | A | C | C | E | A |
| 5th Choice | E | B | E | D | A | E |
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Let a = (-4, 5, 4) and 6 = (1,0, -1).
Find the angle between the vector
1) The exact angle is cos
2) The approximation in radians is
The only problems I need help with ae the last 8 ones, Thanks
Price (S)
The graph below depicts a firm with market power. In the graph, MC represents the firm's marginal costs, ATC represents the average total costs, D represents demand, and MR represents marginal revenue.
110
70
60
50
40
30
20
MC
ATC
D
0
40
50
70
80
95
Quantity/Units
MR
a. At 60 units of output, how much would this profit-maximizing monopolist charge?
b. How many units would it produce to maximize total revenue rather than total profit?
c. What is the maximum quantity this firm can produce without incurring economic losses?
d. Calculate the firm's profit at the profit-maximizing output and price.
e. Why is this firm's marginal revenue curve below its demand curve? Explain.
Chapter 1 Solutions
MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
Ch. 1 - Figure 1-8 shows the preference ballots for an...Ch. 1 - Figure 1-9 shows the preference ballots for an...Ch. 1 - An election is held to choose the Chair of the...Ch. 1 - The student body at Eureka High School is having...Ch. 1 - An election is held using the printed-names format...Ch. 1 - Prob. 6ECh. 1 - Prob. 7ECh. 1 - Table 1-30 shows a conventional preference...Ch. 1 - The Demublican Party is holding its annual...Ch. 1 - The Epicurean Society is holding its annual...
Ch. 1 - Table 1-31 shows the preference schedule for an...Ch. 1 - Table 1-32 shows the preference schedule for an...Ch. 1 - Table 1-33 shows the preference schedule for an...Ch. 1 - Table 1-34 shows the preference schedule for an...Ch. 1 - Table 1-35 shows the preference schedule for an...Ch. 1 - Table1-36 shows the preference schedule for an...Ch. 1 - Table 1-25 see Exercise 3 shows the preference...Ch. 1 - Table 1-26 see Exercise 4 shows the preference...Ch. 1 - Table 1-25 see Exercise 3 shows the preference...Ch. 1 - Table 1-26 see Exercise 4 shows the preference...Ch. 1 - Table 1-31see Exercise 11 shows the preference...Ch. 1 - Table 1-32 see Exercise 12 shows the preference...Ch. 1 - Table 1-33 see Exercise 13 shows the preference...Ch. 1 - Table 1-34 Number of voters 6 6 5 4 3 3 1st A B B...Ch. 1 - Table 1-35 Percent of voters 24 23 19 14 11 9 1st...Ch. 1 - Table 1-36 Percent of voters 25 21 15 12 10 9 8...Ch. 1 - The Heisman Award. Table 1-37 shows the results...Ch. 1 - The 2014 AL Cy Young Award. Table 1-38 shows the...Ch. 1 - An election was held using the conventional Borda...Ch. 1 - Imagine that in the voting for the American League...Ch. 1 - Table 1-31 see Exercise 11 shows the preference...Ch. 1 - Table 1-32 see Exercise 12 shows the preference...Ch. 1 - Table1-33 Number of voters 6 5 4 2 2 2 2 1st C A B...Ch. 1 - Table 1-34 See Exercise 14 shows the preference...Ch. 1 - Table1-39_ shows the preference schedule for an...Ch. 1 - Table1-40_ shows the preference schedule for an...Ch. 1 - Table 1-35 see Exercise 15 shows the preference...Ch. 1 - Table 1-36 see Exercise 16 shows the preference...Ch. 1 - Top-Two Instant-Runoff Voting. Exercises 39 and 40...Ch. 1 - Top-Two Instant-Runoff Voting. Exercises 39 and 40...Ch. 1 - Table 1-31 see Exercise 11 shows the preference...Ch. 1 - Table 1-32 See Exercise 12 shows the preference...Ch. 1 - Table 1-33 see Exercise 13 shows the preference...Ch. 1 - Table 1-34 see Exercise 14 shows the preference...Ch. 1 - Table 1-35 see Exercise 15 shows the preference...Ch. 1 - Table 1-36 see Exercise 16 shows the preference...Ch. 1 - Table 1-39 see Exercise 35 shows the preference...Ch. 1 - Table1-40 see Exercise36 shows the preference...Ch. 1 - An election with five candidates A, B. C, D, and E...Ch. 1 - An election with six candidates A, B, C, D, E, and...Ch. 1 - Use Table 1-41 to illustrate why the Borda count...Ch. 1 - Use Table 1-32 to illustrate why the...Ch. 1 - Use Table 1-42 to illustrate why the plurality...Ch. 1 - Use the Math Club election Example 1.10 to...Ch. 1 - Use Table 1-43 to illustrate why the...Ch. 1 - Explain why the method of pair wise comparisons...Ch. 1 - Prob. 57ECh. 1 - Explain why the plurality method satisfies the...Ch. 1 - Explain why the Borda count method satisfies the...Ch. 1 - Explain why the method of pairwise comparisons...Ch. 1 - Two-candidate elections. Explain why when there...Ch. 1 - Alternative version of the Borda count. The...Ch. 1 - Reverse Borda count. Another commonly used...Ch. 1 - The average ranking. The average ranking of a...Ch. 1 - The 2006 Associated Press college football poll....Ch. 1 - The Pareto criterion. The following fairness...Ch. 1 - The 2003-2004 NBA Rookie of the Year vote. Each...Ch. 1 - Top-two IRV is a variation of the...Ch. 1 - The Coombs method. This method is just like the...Ch. 1 - Bucklin voting. This method was used in the early...Ch. 1 - The 2016 NBA MVP vote. The National Basketball...Ch. 1 - The Condorcet loser criterion. If there is a...Ch. 1 - Consider the following fairness criterion: If a...Ch. 1 - Suppose that the following was proposed as a...Ch. 1 - Consider a modified Borda count where a...
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
Length of a Guy Wire A communications tower is located at the top of a steep hill, as shown. The angle of incli...
Precalculus: Mathematics for Calculus (Standalone Book)
Provide an example of a qualitative variable and an example of a quantitative variable.
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- A well-known company predominantly makes flat pack furniture for students. Variability with the automated machinery means the wood components are cut with a standard deviation in length of 0.45 mm. After they are cut the components are measured. If their length is more than 1.2 mm from the required length, the components are rejected. a) Calculate the percentage of components that get rejected. b) In a manufacturing run of 1000 units, how many are expected to be rejected? c) The company wishes to install more accurate equipment in order to reduce the rejection rate by one-half, using the same ±1.2mm rejection criterion. Calculate the maximum acceptable standard deviation of the new process.arrow_forwardFind the (exact) direction cosines and (rounded to 1 decimal place) direction angles of = (3,7,6)arrow_forwardShade the areas givenarrow_forward
- 5. Let X and Y be independent random variables and let the superscripts denote symmetrization (recall Sect. 3.6). Show that (X + Y) X+ys.arrow_forwardLet a = (-1, -2, -3) and 6 = (-4, 0, 1). Find the component of b onto a.arrow_forwardForces of 9 pounds and 15 pounds act on each other with an angle of 72°. The magnitude of the resultant force The resultant force has an angle of pounds. * with the 9 pound force. The resultant force has an angle of with the 15 pound force. It is best to calculate each angle separately and check by seeing if they add to 72°.arrow_forward
- 1. Sketch the following sets and determine which are domains: (a) |z−2+i| ≤ 1; - (c) Imz> 1; (e) 0≤ arg z≤ л/4 (z ± 0); Ans. (b), (c) are domains. (b) |2z+3| > 4; (d) Im z = 1; - (f) | z − 4| ≥ |z.arrow_forward8. Suppose that the moments of the random variable X are constant, that is, suppose that EX" =c for all n ≥ 1, for some constant c. Find the distribution of X.arrow_forward9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License