Chapter 6, Problem 31P

Suppose the positions of the masses in problem P6-30 are given by

$y_1\left(t\right)=8\sin \left(4\pi t+\frac{\pi }{3}\right)$ and $y_2\left(t\right)=6\cos \left(4\pi t\right)$ ,where $t$ is in seconds.

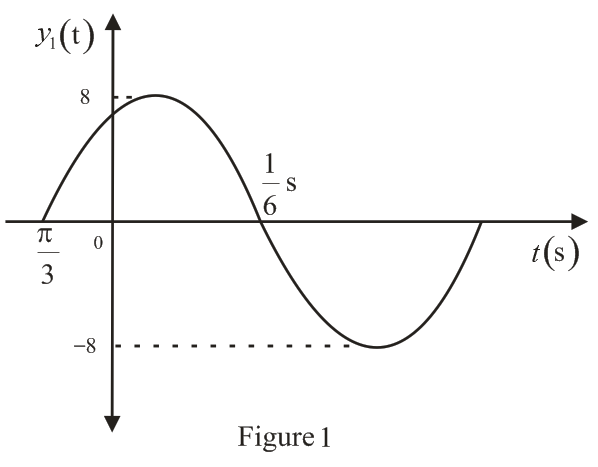
(a) Write down the amplitude, frequency (in Hz), period (in seconds), phase shift (in radians) of the position of the mass $y_1\left(t\right)$.

(b) Plot one cycle of the position $y_1\left(t\right)$, and indicate the earliest time after $t=0$ when the position is zero.

(c) Write $\delta \left(t\right)=y_1\left(t\right)-y_2\left(t\right)$ in the form $\delta \left(t\right)=M\cos \left(4\pi t+\theta °\right)$ ; in other words, find M and $\theta$.