
The tip of a one-link robot is located at
FIGURE P6.1 Rotating one-link robot starting at
To plot:
The
Answer to Problem 1P
The graph for
The graph for
The amplitude of sine and cosine function is
Explanation of Solution
Given:
The tip of a one-link robot is initially located at

Time taken for the robot to move form
A one-link robot is length of
Concept used:
Write the expression for the linear frequency.
Here,
Write the expression for the angular frequency.
Here,
Write the expression for the time period.
Write the expression for
Here,
Write the expression for
Here,
Write the expression for the time shift.
Here,
Calculation:
The one-link robot completes one revolution in
Substitute
Substitute
Therefore, the period of the tip of a one-link robot is
Substitute
Therefore, the frequency is
Since the one-link robot initially start form
Substitute
Here,
Substitute
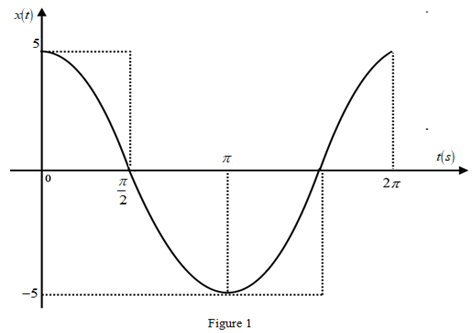
The plot for the
Substitute
Substitute
The plot for the
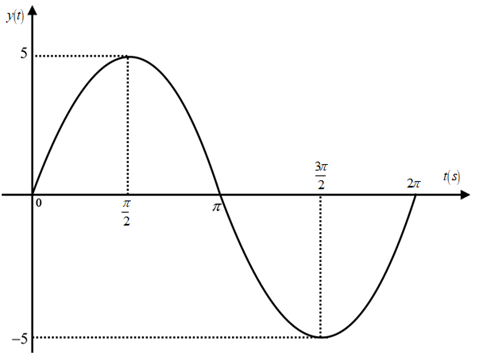
Figure 2
Substitute
Therefore, the time shift of the one-link robot is
The amplitude of sine and cosine function is
Conclusion:
Thus, the graph for
Want to see more full solutions like this?
Chapter 6 Solutions
Introductory Mathematics for Engineering Applications
Additional Math Textbook Solutions
Elementary Statistics: Picturing the World (7th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics (13th Edition)
Introductory Statistics
Elementary Statistics
Thinking Mathematically (6th Edition)
- 5. Find the derivative of f(x) = 6. Evaluate the integral: 3x3 2x²+x— 5. - [dz. x² dx.arrow_forward5. Find the greatest common divisor (GCD) of 24 and 36. 6. Is 121 a prime number? If not, find its factors.arrow_forward13. If a fair coin is flipped, what is the probability of getting heads? 14. A bag contains 3 red balls and 2 blue balls. If one ball is picked at random, what is the probability of picking a red ball?arrow_forward
- 24. What is the value of ¿4, where i 25. Simplify log2 (8). = −1? 26. If P(x) = x³- 2x² + 5x - 10, find P(2). 27. Solve for x: e2x = 7.arrow_forward9. Solve the differential equation: 10. Find the general solution of dy + y = 0. dy 33 dx 3x².arrow_forward3. Differentiate f(x) = x² sin(x). 4. Evaluate the limit: sin(2x) lim xarrow_forward
- 1. Solve for x in the equation: 2. If A = (1/3 2/) 4 x³-3x²+4=0 find the determinant of A.arrow_forward3/4+1/2=arrow_forwardProve that Pleas -- Pleas A collection, Alof countinoes Sunction on a toplogical spacex separetes Point from closed setsinx (f the set S" (V) for KEA and V open set in xx from base for Top onx. @If faixe A} is collection of countinuous fancton on a top space X Wich Separates Points from closed sets then the toplogy on x is weak Top logy.arrow_forward
- @if {fx. KG A} is collection of Countin uous function on a to Polgical Which separates Points Srem closed set then the toplogy onx is the weak toplogy induced by the Map fx. Prove that using dief speParts Point 1 B closed and x&B in X then Sor some kεA fx (X) fx (B). + spacearrow_forwardWhen ever one Point sets in X are closed a collection of functions which separates Points from closed set will separates Point. 18 (prod) is product topological space then xe A (xx, Tx) is homeomorphic to sub space of the Product space (TXA, prod). KeA The Bin Projection map 18: Tx XP is continuous and open but heed hot to be closed. Acale ctioneA} of continuos function ona topogical Space X se partes Points from closed sets inx iff the set (v) for KEA and Vopen set inx from a base for top on X-arrow_forwardWhy are Bartleby experts giving only chatgpt answers?? Why are you wasting our Money and time ?arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
