Chapter 6, Problem 27P

Two voltages ${\nu }_1\left(t\right)=10\sin \left(100\pi t-45°\right)\text{V}$ and ${\nu }_2\left(t\right)=10\sin \left(100\pi t\right)\text{V}$ are applied to the Op—Amp circuit shown in Fig. P6.27.

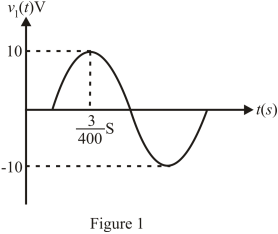
(a) Write down the amplitude, frequency (in Hz), period (in seconds), phase shift (in radians), and time shift (in seconds) of the voltage ${\nu }_1\left(t\right)$.

(b) Plot one cycle of the voltage ${\nu }_1\left(t\right)$, and indicate the earliest time after $t=0$ when the voltage is $10\text{V}$.

(c) The output voltage ${\nu }_0\left(t\right)$ is given by ${\nu }_0\left(t\right)=-\left(\sqrt{2}{\nu }_1\left(t\right)+{\nu }_2\left(t\right)\right)$, write ${\nu }_0\left(t\right)$ in the form ${\nu }_0\left(t\right)=M\cos \left(100\pi t+\theta °\right)$ ; in other words, find M and $\theta$.