
Concept explainers
Find the slope
Answer to Problem 16P
The slope at point B of the given beam using the direct moment-area method is
The deflection at point B of the given beam using the direct moment-area method is
The slope at point C of the given beam using the direct moment-area method is
The deflection at point C of the given beam using the direct moment-area method is
Explanation of Solution
Given information:
The Young’s modulus (E) is 29,000 ksi.
The moment of inertia (I) is
Calculation:
Consider flexural rigidity EI of the beam is constant.
Show the free body diagram of the given beam as in Figure (1).
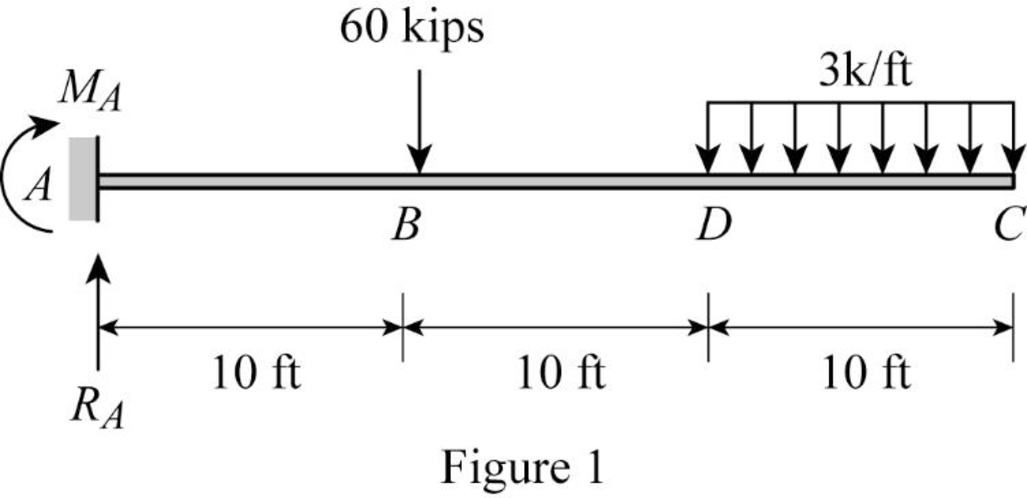
Refer Figure 1,
Consider upward is positive and downward is negative.
Consider clockwise is negative and counterclowise is positive.
Since support C is a free end there is no reaction.
Determine the bending moment at A;
Determine the bending moment at B;
Determine the moment at D;
Determine the bending moment at C;
Show the
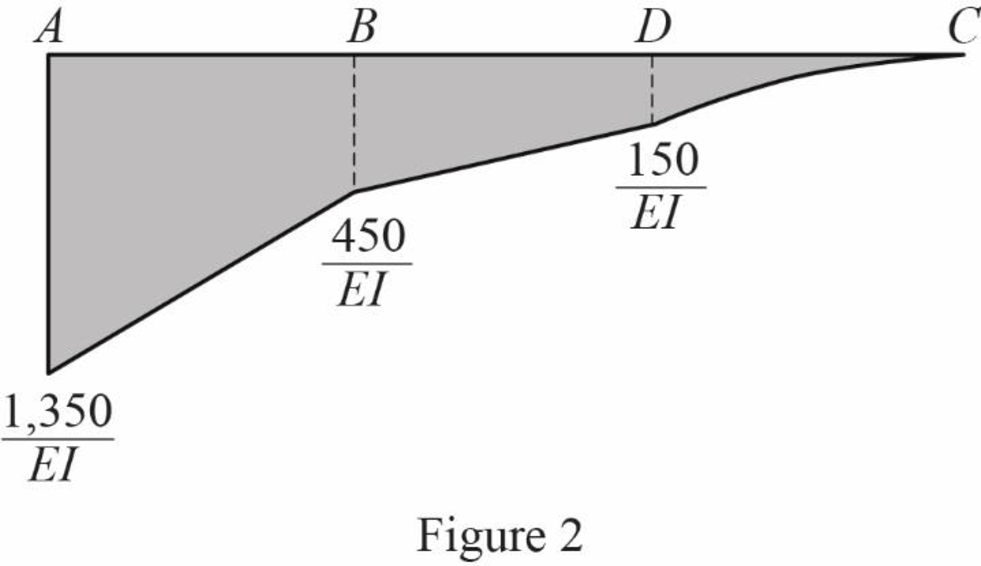
Elastic curve:
The sign of
Show the elastic curve diagram as in Figure (3).
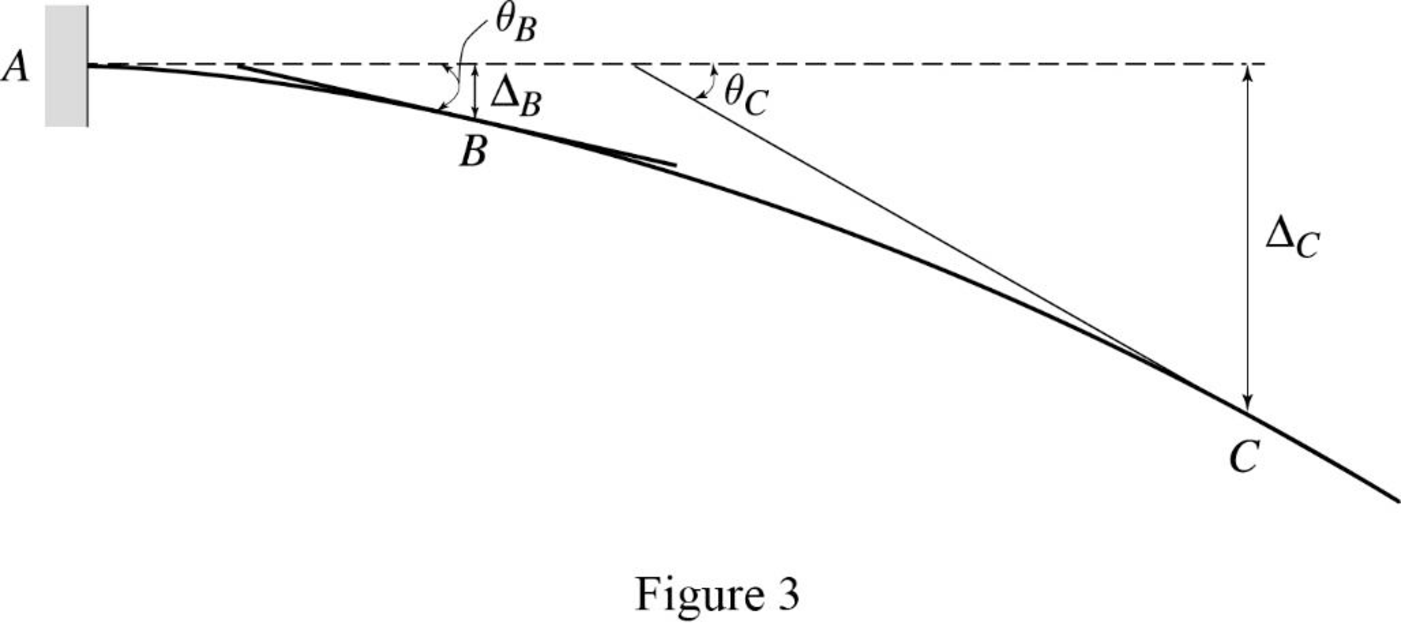
The slope at point B can be calculated by evaluating the change in slope between A and B.
Express the change in slope using the first moment-area theorem as follows:
Here, b is the width of the respective triangle and rectangle and h is the height of the respective triangle and rectangle.
Substitute 10 ft for b,
Determine the slope at B using the relation;
Substitute
Hence, the slope at point B is
The deflection of B with respect to the undeforemd axis of the beam is equal to the tangential deviation of B from the tangent at A.
Express the deflection at B using the second moment-area theorem as follows:
Substitute 10 ft for b,
Determine the deflection at B using the relation;
Substitute
Hence, the deflection at B is
Express the change in slope using the first moment-area theorem as follows:
Here, b is the width and h is the height of the rectangle, triangle, and parabola.
Substitute
Determine the slope at C using the relation;
Substitute
Hence, the slope at point C is
The deflection of C with respect to the undeforemd axis of the beam is equal to the tangential deviation of C from the tangent at A.
Express the deflection at C using the second moment-area theorem as follows:
Determine the deflection at C using the relation;
Substitute
Hence, the deflection at C is
Want to see more full solutions like this?
Chapter 6 Solutions
Structural Analysis, 5th Edition
- Determine the design resistance to transverse force F,Rdarrow_forwardAs a structural engineer, your task is to design an optimum section that has sufficient resistance to the applied loading for the primary beam proposed in Figure 1. A UB in grade S275 steel is required for the unrestraint beam to carry the ultimate loads over the given span. Choose an optimumUB section and justify your selection. You are required to submit a design analysis by considering bending, shear, transverse force, and deflection checking for the selected member based on Eurocode 3 and the assumption of support condition and loading must be clearly stated. P=15 kN. a 2 m. b=3m ·L· ·b. Figure 1 Simply supported steel beamarrow_forwardWhy is it important to establish logical relationships between tasks when developing a construction schedule?arrow_forward
- For the gravity concrete dam shown in the figure, the following data are available: - Unit weight of concrete (Yeone) = 2.4 ton/m³ Neglect( Wave pressure, silt pressure, ice force and earth quake force) -0.65, (Ywater) 1 ton/m³ Find factor of safety against sliding and overturning (F.Said & F.Sover), If heel and toe stresses (Pais & Pmas) are 57.17ton/m2 and 84.53 ton/m² respectively. w.s.l 83m 10m 80m 8m Solve on paper step by step with sketcharrow_forwardWhy is proper planning important when developing a baseline construction project schedule?arrow_forwardDetermine the minimum possible surface area of a secondary clarifier treating activated sludge with a design influent flow rate (Q) of 1,000 m³/d, a return activated sludge (RAS) recycling ratio of 25%, and a mixed liquor total suspended solids (MLSS) concentration of 4,000 mg/L, if the overflow rate must be less than 33 m/d and the solids loading rate must be less than 250 kg/m²/d. Express your answer in m² and round up to the next integer.arrow_forward
- Estimate the required air flow rate for the new activated sludge plant at Pea Ridge (Problems 23-223-723-10, and 23-13). The flow rate is 8,450 m³/day, the concentration of bCOD going into the system (So) is 137 mg/L, the concentration of bCOD leaving the system (S) is 16.3 mg/L, and the mass of cells produced per day (Pxvss) is 277.4 kg/d. Use the following assumptions to estimate the required air flow rate: . Clean water correction, a = 0.50 . Salinity correction, B = 0.95 Fouling factor = 0.9 Wastewater temperature = 12°C Atmospheric pressure = 101.325 kPa .Elevation 500 m . Depth of aerator = 5.6 m Operating DO 2.0 mg/L Percent oxygen leaving aeration tank - 19% ■ Manufacturer's SOTR = 535 kg/d Manufacturer's air flow rate at standard conditions 50 m³/d - aerator Express your answer with the units of m³/d and round to the nearest integer.arrow_forwardDetermine the required solids retention time (SRT) of a completely mixed activated sludge aeration tank for a conventional activated sludge system treating a design flow rate of 34,560 m³/d, where the effluent standards are 30.0 mg/L for BODs and 30.0 mg/L for total suspended solids (TSS). Assume that the BOD5 of the effluent TSS is 70% of the TSS concentration. Assume the BODs concentration leaving the primary clarifier is 128 mg/L that the MLVSS concentration (X₂) is 2,500 mg/L. Assume the following values for the growth constants: Ks 100 mg/L BODS ⚫ Hm - 2.5 d 1 kd = 0.050 d 1 Y = 0.50 mg VSS/mg BODs removed Express your answer in days and round to the nearest 0.1.arrow_forwardQ1: Figure below shows loaded beam with its cross-section area, (A) Draw shear force and bending moment diagrams, stating the main values, (B) Find central slope and deflection, (C) Sketch the distribution of shear stress at left support, (D) Find maximum tensile and compressive bending stresses set up in beam at right support. E-205GN/m² P1 P2 P3 W1 W2 Lin Lin # A Length in (m) and loads in kN 3a a 2a 2a (Cross-section area, All dimensions in (mm))arrow_forward
- Estimate the mass of oxygen to be supplied for a new activated sludge plant at Pea Ridge to treat a flow rate of 8,450 m³/day. Assume that the concentration of bCOD going into the system (So) is 137 mg/L, that the bCOD leaving the system (S) is 16.3 mg/L, and that the mass of cells produced per day (Pxvss) is 277.4 kg/d. Express your answer in kg/day and round to the nearest integer.arrow_forward*10-4. Determine the internal moments at the supports A, B, and C, then draw the moment diagram. Assume A is pinned, and B and C are rollers. El is constant. 3 k/ft 8 ft- 8 ft -4 ft-arrow_forwardQ2: Determine the change in dimensions in each section of the bar shown in figure. The portion AB is circular section and portion BC is rectangular section. E=115GN/m², v=0.33. L1 L2 P2+ P2 B Q3: A block is subjected to the stresses as shown in figure, find: principal stresses, shear stress with their directions and the normal and shear stresses on a plane inclined at 0. All stresses in MPa. (Confirm your answer by means of Mohr's stress circle). Txy 30 Note: (1) For all questions the student can choose any values of P1, P2, P3, W1, W2, a, σ (MPa), Txy (MPa), 0°, length and the dimensions of cross section area.arrow_forward
