
Concept explainers
To graph:the two lines appear to intersect each other with the help of given information.
Answer to Problem 36PPE
The lines intersect each other.
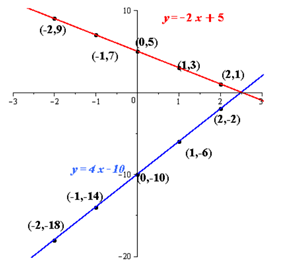
Explanation of Solution
Given information:
Given table:
| X | Y |
| -2 | 9 |
| -1 | 7 |
| 0 | 5 |
| 1 | 3 |
| 2 | 1 |
| X | Y |
| -2 | -18 |
| -1 | -14 |
| 0 | -10 |
| 1 | -6 |
| 2 | -2 |
Calculation:
Consider the table provided for the two lines in the textbook.
Let the slope
Now solve to find the values of
Use the first table,
Put the points (-2,9) and (-1,7) from first table in
Hence,
After solving the above equations,
Use the second table,
Put the points
Hence,
After solving the above equations,
Thus, the two equations become as follows,
Plot the above lines with the use of table provided in textbook,
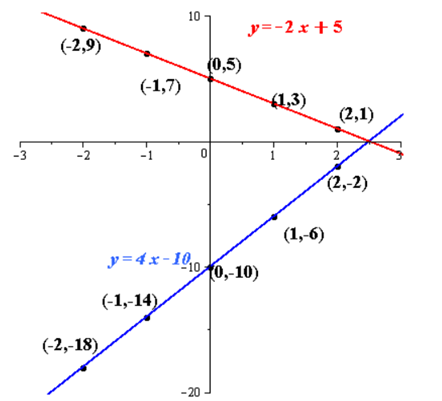
From the above figure it is that the lines intersect each other.
Chapter 5 Solutions
EP ALGEBRA 1-ETEXT ACCESS
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
Calculus: Early Transcendentals (2nd Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Algebra and Trigonometry (6th Edition)
A First Course in Probability (10th Edition)
Elementary Statistics (13th Edition)
- Directions: Use the equation A = Pet to answer each question and be sure to show all your work. 1. If $5,000 is deposited in an account that receives 6.1% interest compounded continuously, how much money is in the account after 6 years? 2. After how many years will an account have $12,000 if $6,000 is deposited, and the account receives 3.8% interest compounded continuously? 3. Abigail wants to save $15,000 to buy a car in 7 years. If she deposits $10,000 into an account that receives 5.7% interest compounded continuously, will she have enough money in 7 years? 4. Daniel deposits $8,000 into a continuously compounding interest account. After 18 years, there is $13,006.40 in the account. What was the interest rate? 5. An account has $26,000 after 15 years. The account received 2.3% interest compounded continuously. How much was deposited initially?arrow_forwardTRIANGLES INDEPENDENT PRACTICE ription Criangle write and cow Using each picture or description of triangle write and solve an equation in ordering the number of degrees in each angle TRIANGLE EQUATION & WORK ANGLE MEASURES A B -(7x-2)° (4x) (3x)° (5x − 10) C (5x – 2) (18x) E 3. G 4. H (16x)° LL 2A= 2B= ZE=arrow_forwardAnswer ASAP and every part, please. Structures.arrow_forwardI want to learn this topic l dont know anything about itarrow_forwardSolve the linear system of equations attached using Gaussian elimination (not Gauss-Jordan) and back subsitution. Remember that: A matrix is in row echelon form if Any row that consists only of zeros is at the bottom of the matrix. The first non-zero entry in each other row is 1. This entry is called aleading 1. The leading 1 of each row, after the first row, lies to the right of the leading 1 of the previous row.arrow_forwardPRIMERA EVALUACIÓN SUMATIVA 10. Determina la medida de los ángulos in- teriores coloreados en cada poligono. ⚫ Octágono regular A 11. Calcula es número de lados qu poligono regular, si la medida quiera de sus ángulos internos • a=156° A= (-2x+80 2 156 180- 360 0 = 24-360 360=24° • a = 162° 1620-180-360 6=18-360 360=19 2=360= 18 12. Calcula las medida ternos del cuadrilá B X+5 x+10 A X+X+ Sx+6 5x=3 x=30 0 лаб • Cuadrilátero 120° 110° • α = 166° 40' 200=180-360 0 = 26-360 360=20 ひ=360 20 18 J 60° ⚫a=169° 42' 51.43" 169.4143180-340 0 = 10.29 54-360 360 10.2857 2=360 10.2857 @Saarrow_forwardPlease help I'm a working mom trying to help my son last minute (6th grader)! Need help with the blank ones and check the ones he got with full calculation so we can use it to study! Especially the mixed number fractions cause I'm rusty. Thanks in advance!arrow_forward|| 38 5층-11- 6 4 7 2 6arrow_forwardMs.sally has 12 studentsMr Franklin has twice as many students as Ms. Sally.how many students does Mr Franklin have?arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





