EP ALGEBRA 1-ETEXT ACCESS
EP ALGEBRA 1-ETEXT ACCESS
11th Edition
ISBN: 9780133216455
Author: Charles
Publisher: SAVVAS L
bartleby

Concept explainers

Bar Graphs
A bar graph is a chart or graphical representation of data. A bar chart, also known as a bar graph, is a graph or chart that displays categorical data using rectangular bars with heights or lengths equal to the values they represent. Typically, bar graph…
bartleby

Videos

Question
Book Icon
Chapter 5, Problem 35CR

(a)

To determine

To plot: The scatter plot of given data.

(a)

Expert Solution
Check Mark

Explanation of Solution

Given information:

Table:

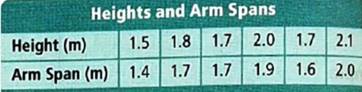
  EP ALGEBRA 1-ETEXT ACCESS, Chapter 5, Problem 35CR , additional homework tip 1

Graph:

The graph of the table:

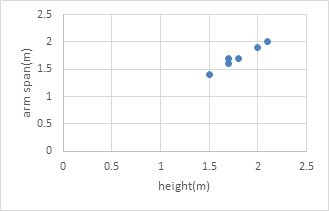
  EP ALGEBRA 1-ETEXT ACCESS, Chapter 5, Problem 35CR , additional homework tip 2

(b)

To determine

To find: The equation of trend line of the graph.

(b)

Expert Solution
Check Mark

Answer to Problem 35CR

The equation of trend line is y=x−0.1

Explanation of Solution

Given information:

   ( x 1 , y 1 );(1.5,1.4) ( x 2 , y 2 );(2.1,2.0)

Formula used:

   y=mx+C m= y 2 − y 1 x 2 − x 1

Calculation:

   y=mx+C m= y 2 − y 1 x 2 − x 1 m= 2−1.4 2.1−1.5 m=1 C=−0.1 y=x−0.1

Conclusion:

The equation of trend line is y=x−0.1

(c)

To determine

To find: The Arm spam of someone who is 1.6m tall.

(c)

Expert Solution
Check Mark

Answer to Problem 35CR

Arm spam of someone who is 1.6m tall is 1.5m.

Explanation of Solution

Given information:

   y=x−0.1

Calculation:

Arm spam of someone who is 1.6m tall:

   y=1.6−0.1 y=1.5m

Conclusion:

Arm spam of someone who is 1.6m tall is 1.5m.

(d)

To determine

To find: The Arm span of someone who is 2.2m tall.

(d)

Expert Solution
Check Mark

Answer to Problem 35CR

Arm span of someone who is 2.2m tall is 2.1m.

Explanation of Solution

Given information:

   y=x−0.1

Calculation:

Arm span of someone who is 2.2m tall:

   y=x−0.1 y=2.2−0.1 y=2.1m

Conclusion:

Arm span of someone who is 2.2m tall is 2.1m.

Previous
Chapter 5, Problem 34CR
Next
Chapter 5, Problem 36CR

Chapter 5 Solutions

EP ALGEBRA 1-ETEXT ACCESS

Ch. 5.1 - Prob. 1PCh. 5.1 - Prob. 2PCh. 5.1 - Prob. 3PCh. 5.1 - Prob. 4PCh. 5.1 - Prob. 1LCCh. 5.1 - Prob. 2LCCh. 5.1 - Prob. 3LCCh. 5.1 - Prob. 4LCCh. 5.1 - Prob. 5LCCh. 5.1 - Prob. 6LC
Ch. 5.1 - Prob. 7LCCh. 5.1 - Prob. 8PPECh. 5.1 - Prob. 9PPECh. 5.1 - Prob. 10PPECh. 5.1 - Prob. 11PPECh. 5.1 - Prob. 12PPECh. 5.1 - Prob. 13PPECh. 5.1 - Prob. 14PPECh. 5.1 - Prob. 15PPECh. 5.1 - Prob. 16PPECh. 5.1 - Prob. 17PPECh. 5.1 - Prob. 18PPECh. 5.1 - Prob. 19PPECh. 5.1 - Prob. 20PPECh. 5.1 - Prob. 21PPECh. 5.1 - Prob. 22PPECh. 5.1 - Prob. 23PPECh. 5.1 - Prob. 24PPECh. 5.1 - Prob. 25PPECh. 5.1 - Prob. 26PPECh. 5.1 - Prob. 27PPECh. 5.1 - Prob. 28PPECh. 5.1 - Prob. 29PPECh. 5.1 - Prob. 30PPECh. 5.1 - Prob. 31PPECh. 5.1 - Prob. 32PPECh. 5.1 - Prob. 33PPECh. 5.1 - Prob. 34PPECh. 5.1 - Prob. 35PPECh. 5.1 - Prob. 36PPECh. 5.1 - Prob. 37PPECh. 5.1 - Prob. 38PPECh. 5.1 - Prob. 39PPECh. 5.1 - Prob. 40PPECh. 5.1 - Prob. 41PPECh. 5.1 - Prob. 42PPECh. 5.1 - Prob. 43PPECh. 5.1 - Prob. 44PPECh. 5.1 - Prob. 45PPECh. 5.1 - Prob. 46PPECh. 5.1 - Prob. 47PPECh. 5.1 - Prob. 48PPECh. 5.1 - Prob. 49PPECh. 5.1 - Prob. 50PPECh. 5.1 - Prob. 51PPECh. 5.1 - Prob. 52PPECh. 5.1 - Prob. 53PPECh. 5.1 - Prob. 54PPECh. 5.1 - Prob. 55PPECh. 5.1 - Prob. 56PPECh. 5.1 - Prob. 57PPECh. 5.1 - Prob. 58PPECh. 5.1 - Prob. 1MPCh. 5.2 - Prob. 1PCh. 5.2 - Prob. 2PCh. 5.2 - Prob. 3PCh. 5.2 - Prob. 4PCh. 5.2 - Prob. 1LCCh. 5.2 - Prob. 2LCCh. 5.2 - Prob. 3LCCh. 5.2 - Prob. 4LCCh. 5.2 - Prob. 5LCCh. 5.2 - Prob. 6LCCh. 5.2 - Prob. 7LCCh. 5.2 - Prob. 8LCCh. 5.2 - Prob. 9PPECh. 5.2 - Prob. 10PPECh. 5.2 - Prob. 11PPECh. 5.2 - Prob. 12PPECh. 5.2 - Prob. 13PPECh. 5.2 - Prob. 14PPECh. 5.2 - Prob. 15PPECh. 5.2 - Prob. 16PPECh. 5.2 - Prob. 17PPECh. 5.2 - Prob. 18PPECh. 5.2 - Prob. 19PPECh. 5.2 - Prob. 20PPECh. 5.2 - Prob. 21PPECh. 5.2 - Prob. 22PPECh. 5.2 - Prob. 23PPECh. 5.2 - Prob. 24PPECh. 5.2 - Prob. 25PPECh. 5.2 - Prob. 26PPECh. 5.2 - Prob. 27PPECh. 5.2 - Prob. 28PPECh. 5.2 - Prob. 29PPECh. 5.2 - Prob. 30PPECh. 5.2 - Prob. 31PPECh. 5.2 - Prob. 32PPECh. 5.2 - Prob. 33PPECh. 5.2 - Prob. 34PPECh. 5.2 - Prob. 35PPECh. 5.2 - Prob. 36PPECh. 5.2 - Prob. 37PPECh. 5.2 - Prob. 38PPECh. 5.2 - Prob. 39PPECh. 5.2 - Prob. 40PPECh. 5.2 - Prob. 41PPECh. 5.2 - Prob. 42PPECh. 5.2 - Prob. 43PPECh. 5.2 - Prob. 44PPECh. 5.2 - Prob. 45PPECh. 5.2 - Prob. 46PPECh. 5.2 - Prob. 47PPECh. 5.2 - Prob. 48STPCh. 5.2 - Prob. 49STPCh. 5.2 - Prob. 50STPCh. 5.2 - Prob. 51STPCh. 5.2 - Prob. 52MRCh. 5.2 - Prob. 53MRCh. 5.2 - Prob. 54MRCh. 5.2 - Prob. 55MRCh. 5.2 - Prob. 56MRCh. 5.2 - Prob. 57MRCh. 5.2 - Prob. 58MRCh. 5.2 - Prob. 59MRCh. 5.3 - Prob. 1CBCh. 5.3 - Prob. 2CBCh. 5.3 - Prob. 3CBCh. 5.3 - Prob. 4CBCh. 5.3 - Prob. 5CBCh. 5.3 - Prob. 6CBCh. 5.3 - Prob. 7CBCh. 5.3 - Prob. 1PCh. 5.3 - Prob. 2PCh. 5.3 - Prob. 3PCh. 5.3 - Prob. 4PCh. 5.3 - Prob. 5PCh. 5.3 - Prob. 6PCh. 5.3 - Prob. 1LCCh. 5.3 - Prob. 2LCCh. 5.3 - Prob. 3LCCh. 5.3 - Prob. 4LCCh. 5.3 - Prob. 5LCCh. 5.3 - Prob. 6LCCh. 5.3 - Prob. 7PPECh. 5.3 - Prob. 8PPECh. 5.3 - Prob. 9PPECh. 5.3 - Prob. 10PPECh. 5.3 - Prob. 11PPECh. 5.3 - Prob. 12PPECh. 5.3 - Prob. 13PPECh. 5.3 - Prob. 14PPECh. 5.3 - Prob. 15PPECh. 5.3 - Prob. 16PPECh. 5.3 - Prob. 17PPECh. 5.3 - Prob. 18PPECh. 5.3 - Prob. 19PPECh. 5.3 - Prob. 20PPECh. 5.3 - Prob. 21PPECh. 5.3 - Prob. 22PPECh. 5.3 - Prob. 23PPECh. 5.3 - Prob. 24PPECh. 5.3 - Prob. 25PPECh. 5.3 - Prob. 26PPECh. 5.3 - Prob. 27PPECh. 5.3 - Prob. 28PPECh. 5.3 - Prob. 29PPECh. 5.3 - Prob. 30PPECh. 5.3 - Prob. 31PPECh. 5.3 - Prob. 32PPECh. 5.3 - Prob. 33PPECh. 5.3 - Prob. 34PPECh. 5.3 - Prob. 35PPECh. 5.3 - Prob. 36PPECh. 5.3 - Prob. 37PPECh. 5.3 - Prob. 38PPECh. 5.3 - Prob. 39PPECh. 5.3 - Prob. 40PPECh. 5.3 - Prob. 41PPECh. 5.3 - Prob. 42PPECh. 5.3 - Prob. 43PPECh. 5.3 - Prob. 44PPECh. 5.3 - Prob. 45PPECh. 5.3 - Prob. 46PPECh. 5.3 - Prob. 47PPECh. 5.3 - Prob. 48PPECh. 5.3 - Prob. 49PPECh. 5.3 - Prob. 50PPECh. 5.3 - Prob. 51PPECh. 5.3 - Prob. 52PPECh. 5.3 - Prob. 53PPECh. 5.3 - Prob. 54PPECh. 5.3 - Prob. 55PPECh. 5.3 - Prob. 56PPECh. 5.3 - Prob. 57PPECh. 5.3 - Prob. 58PPECh. 5.3 - Prob. 59PPECh. 5.3 - Prob. 60PPECh. 5.3 - Prob. 61PPECh. 5.3 - Prob. 62PPECh. 5.3 - Prob. 63STPCh. 5.3 - Prob. 64STPCh. 5.3 - Prob. 65STPCh. 5.3 - Prob. 66STPCh. 5.3 - Prob. 67STPCh. 5.3 - Prob. 68MRCh. 5.3 - Prob. 69MRCh. 5.3 - Prob. 70MRCh. 5.3 - Prob. 71MRCh. 5.3 - Prob. 72MRCh. 5.3 - Prob. 73MRCh. 5.3 - Prob. 74MRCh. 5.3 - Prob. 75MRCh. 5.3 - Prob. 76MRCh. 5.3 - Prob. 77MRCh. 5.4 - Prob. 1PCh. 5.4 - Prob. 2PCh. 5.4 - Prob. 3PCh. 5.4 - Prob. 4PCh. 5.4 - Prob. 1LCCh. 5.4 - Prob. 2LCCh. 5.4 - Prob. 3LCCh. 5.4 - Prob. 4LCCh. 5.4 - Prob. 5LCCh. 5.4 - Prob. 6LCCh. 5.4 - Prob. 7LCCh. 5.4 - Prob. 8PPECh. 5.4 - Prob. 9PPECh. 5.4 - Prob. 10PPECh. 5.4 - Prob. 11PPECh. 5.4 - Prob. 12PPECh. 5.4 - Prob. 13PPECh. 5.4 - Prob. 14PPECh. 5.4 - Prob. 15PPECh. 5.4 - Prob. 16PPECh. 5.4 - Prob. 17PPECh. 5.4 - Prob. 18PPECh. 5.4 - Prob. 19PPECh. 5.4 - Prob. 20PPECh. 5.4 - Prob. 21PPECh. 5.4 - Prob. 22PPECh. 5.4 - Prob. 23PPECh. 5.4 - Prob. 24PPECh. 5.4 - Prob. 25PPECh. 5.4 - Prob. 26PPECh. 5.4 - Prob. 27PPECh. 5.4 - Prob. 28PPECh. 5.4 - Prob. 29PPECh. 5.4 - Prob. 30PPECh. 5.4 - Prob. 31PPECh. 5.4 - Prob. 32PPECh. 5.4 - Prob. 1MPCh. 5.4 - Prob. 1MCQCh. 5.4 - Prob. 2MCQCh. 5.4 - Prob. 3MCQCh. 5.4 - Prob. 4MCQCh. 5.4 - Prob. 5MCQCh. 5.4 - Prob. 6MCQCh. 5.4 - Prob. 7MCQCh. 5.4 - Prob. 8MCQCh. 5.4 - Prob. 9MCQCh. 5.4 - Prob. 10MCQCh. 5.4 - Prob. 11MCQCh. 5.4 - Prob. 12MCQCh. 5.4 - Prob. 13MCQCh. 5.4 - Prob. 14MCQCh. 5.4 - Prob. 15MCQCh. 5.4 - Prob. 16MCQCh. 5.4 - Prob. 17MCQCh. 5.4 - Prob. 18MCQCh. 5.4 - Prob. 19MCQCh. 5.4 - Prob. 20MCQCh. 5.4 - Prob. 21MCQCh. 5.4 - Prob. 22MCQCh. 5.4 - Prob. 23MCQCh. 5.4 - Prob. 24MCQCh. 5.4 - Prob. 25MCQCh. 5.4 - Prob. 26MCQCh. 5.5 - Prob. 1PCh. 5.5 - Prob. 2PCh. 5.5 - Prob. 3PCh. 5.5 - Prob. 4PCh. 5.5 - Prob. 5PCh. 5.5 - Prob. 1LCCh. 5.5 - Prob. 2LCCh. 5.5 - Prob. 3LCCh. 5.5 - Prob. 4LCCh. 5.5 - Prob. 5LCCh. 5.5 - Prob. 6LCCh. 5.5 - Prob. 7LCCh. 5.5 - Prob. 8PPECh. 5.5 - Prob. 9PPECh. 5.5 - Prob. 10PPECh. 5.5 - Prob. 11PPECh. 5.5 - Prob. 12PPECh. 5.5 - Prob. 13PPECh. 5.5 - Prob. 14PPECh. 5.5 - Prob. 15PPECh. 5.5 - Prob. 16PPECh. 5.5 - Prob. 17PPECh. 5.5 - Prob. 18PPECh. 5.5 - Prob. 19PPECh. 5.5 - Prob. 20PPECh. 5.5 - Prob. 21PPECh. 5.5 - Prob. 22PPECh. 5.5 - Prob. 23PPECh. 5.5 - Prob. 24PPECh. 5.5 - Prob. 25PPECh. 5.5 - Prob. 26PPECh. 5.5 - Prob. 27PPECh. 5.5 - Prob. 28PPECh. 5.5 - Prob. 29PPECh. 5.5 - Prob. 30PPECh. 5.5 - Prob. 31PPECh. 5.5 - Prob. 32PPECh. 5.5 - Prob. 33PPECh. 5.5 - Prob. 34PPECh. 5.5 - Prob. 35PPECh. 5.5 - Prob. 36PPECh. 5.5 - Prob. 37PPECh. 5.5 - Prob. 38PPECh. 5.5 - Prob. 39PPECh. 5.5 - Prob. 40PPECh. 5.5 - Prob. 41PPECh. 5.5 - Prob. 42PPECh. 5.5 - Prob. 43PPECh. 5.5 - Prob. 44PPECh. 5.5 - Prob. 45PPECh. 5.5 - Prob. 46PPECh. 5.5 - Prob. 47PPECh. 5.5 - Prob. 48PPECh. 5.5 - Prob. 49PPECh. 5.5 - Prob. 50PPECh. 5.5 - Prob. 51PPECh. 5.5 - Prob. 52PPECh. 5.5 - Prob. 53PPECh. 5.5 - Prob. 54PPECh. 5.5 - Prob. 55PPECh. 5.5 - Prob. 56PPECh. 5.5 - Prob. 57PPECh. 5.5 - Prob. 58PPECh. 5.5 - Prob. 59PPECh. 5.5 - Prob. 60PPECh. 5.5 - Prob. 61PPECh. 5.5 - Prob. 62PPECh. 5.5 - Prob. 63PPECh. 5.5 - Prob. 64STPCh. 5.5 - Prob. 65STPCh. 5.5 - Prob. 66STPCh. 5.5 - Prob. 67STPCh. 5.5 - Prob. 68STPCh. 5.5 - Prob. 69MRCh. 5.5 - Prob. 70MRCh. 5.5 - Prob. 71MRCh. 5.5 - Prob. 72MRCh. 5.5 - Prob. 73MRCh. 5.5 - Prob. 74MRCh. 5.5 - Prob. 75MRCh. 5.5 - Prob. 76MRCh. 5.5 - Prob. 77MRCh. 5.5 - Prob. 1CBCh. 5.5 - Prob. 2CBCh. 5.5 - Prob. 3CBCh. 5.5 - Prob. 4CBCh. 5.5 - Prob. 5CBCh. 5.5 - Prob. 6CBCh. 5.5 - Prob. 7CBCh. 5.5 - Prob. 8CBCh. 5.5 - Prob. 9CBCh. 5.5 - Prob. 10CBCh. 5.5 - Prob. 11CBCh. 5.5 - Prob. 12CBCh. 5.5 - Prob. 13CBCh. 5.5 - Prob. 14CBCh. 5.5 - Prob. 15CBCh. 5.5 - Prob. 16CBCh. 5.5 - Prob. 17CBCh. 5.5 - Prob. 18CBCh. 5.5 - Prob. 19CBCh. 5.6 - Prob. 1PCh. 5.6 - Prob. 2PCh. 5.6 - Prob. 3PCh. 5.6 - Prob. 4PCh. 5.6 - Prob. 1LCCh. 5.6 - Prob. 2LCCh. 5.6 - Prob. 3LCCh. 5.6 - Prob. 4LCCh. 5.6 - Prob. 5LCCh. 5.6 - Prob. 6LCCh. 5.6 - Prob. 7PPECh. 5.6 - Prob. 8PPECh. 5.6 - Prob. 9PPECh. 5.6 - Prob. 10PPECh. 5.6 - Prob. 11PPECh. 5.6 - Prob. 12PPECh. 5.6 - Prob. 13PPECh. 5.6 - Prob. 14PPECh. 5.6 - Prob. 15PPECh. 5.6 - Prob. 16PPECh. 5.6 - Prob. 17PPECh. 5.6 - Prob. 18PPECh. 5.6 - Prob. 19PPECh. 5.6 - Prob. 20PPECh. 5.6 - Prob. 21PPECh. 5.6 - Prob. 22PPECh. 5.6 - Prob. 23PPECh. 5.6 - Prob. 24PPECh. 5.6 - Prob. 25PPECh. 5.6 - Prob. 26PPECh. 5.6 - Prob. 27PPECh. 5.6 - Prob. 28PPECh. 5.6 - Prob. 29PPECh. 5.6 - Prob. 30PPECh. 5.6 - Prob. 31PPECh. 5.6 - Prob. 32PPECh. 5.6 - Prob. 33PPECh. 5.6 - Prob. 34PPECh. 5.6 - Prob. 35PPECh. 5.6 - Prob. 36PPECh. 5.6 - Prob. 37PPECh. 5.6 - Prob. 38STPCh. 5.6 - Prob. 39STPCh. 5.6 - Prob. 40STPCh. 5.6 - Prob. 41MRCh. 5.6 - Prob. 42MRCh. 5.6 - Prob. 43MRCh. 5.6 - Prob. 44MRCh. 5.6 - Prob. 45MRCh. 5.6 - Prob. 46MRCh. 5.6 - Prob. 47MRCh. 5.7 - Prob. 1PCh. 5.7 - Prob. 2PCh. 5.7 - Prob. 3PCh. 5.7 - Prob. 4PCh. 5.7 - Prob. 1LCCh. 5.7 - Prob. 2LCCh. 5.7 - Prob. 3LCCh. 5.7 - Prob. 4LCCh. 5.7 - Prob. 5LCCh. 5.7 - Prob. 6LCCh. 5.7 - Prob. 7PPECh. 5.7 - Prob. 8PPECh. 5.7 - Prob. 9PPECh. 5.7 - Prob. 10PPECh. 5.7 - Prob. 11PPECh. 5.7 - Prob. 12PPECh. 5.7 - Prob. 13PPECh. 5.7 - Prob. 14PPECh. 5.7 - Prob. 15PPECh. 5.7 - Prob. 16PPECh. 5.7 - Prob. 17PPECh. 5.7 - Prob. 18PPECh. 5.7 - Prob. 19PPECh. 5.7 - Prob. 20PPECh. 5.7 - Prob. 21PPECh. 5.7 - Prob. 22PPECh. 5.7 - Prob. 23STPCh. 5.7 - Prob. 24STPCh. 5.7 - Prob. 25STPCh. 5.7 - Prob. 26STPCh. 5.7 - Prob. 27MRCh. 5.7 - Prob. 28MRCh. 5.7 - Prob. 29MRCh. 5.7 - Prob. 30MRCh. 5.7 - Prob. 31MRCh. 5.7 - Prob. 32MRCh. 5.7 - Prob. 33MRCh. 5.7 - Prob. 5CBCh. 5.7 - Prob. 6CBCh. 5.8 - Prob. 1PCh. 5.8 - Prob. 2PCh. 5.8 - Prob. 3PCh. 5.8 - Prob. 4PCh. 5.8 - Prob. 1LCCh. 5.8 - Prob. 2LCCh. 5.8 - Prob. 3LCCh. 5.8 - Prob. 4LCCh. 5.8 - Prob. 5LCCh. 5.8 - Prob. 6PPECh. 5.8 - Prob. 7PPECh. 5.8 - Prob. 8PPECh. 5.8 - Prob. 9PPECh. 5.8 - Prob. 10PPECh. 5.8 - Prob. 11PPECh. 5.8 - Prob. 12PPECh. 5.8 - Prob. 13PPECh. 5.8 - Prob. 14PPECh. 5.8 - Prob. 15PPECh. 5.8 - Prob. 16PPECh. 5.8 - Prob. 17PPECh. 5.8 - Prob. 18PPECh. 5.8 - Prob. 19PPECh. 5.8 - Prob. 20PPECh. 5.8 - Prob. 21PPECh. 5.8 - Prob. 22PPECh. 5.8 - Prob. 23PPECh. 5.8 - Prob. 24PPECh. 5.8 - Prob. 25PPECh. 5.8 - Prob. 26PPECh. 5.8 - Prob. 27PPECh. 5.8 - Prob. 28PPECh. 5.8 - Prob. 29PPECh. 5.8 - Prob. 30PPECh. 5.8 - Prob. 31PPECh. 5.8 - Prob. 32PPECh. 5.8 - Prob. 33PPECh. 5.8 - Prob. 34PPECh. 5.8 - Prob. 35PPECh. 5.8 - Prob. 36PPECh. 5.8 - Prob. 37PPECh. 5.8 - Prob. 38STPCh. 5.8 - Prob. 39STPCh. 5.8 - Prob. 40STPCh. 5.8 - Prob. 41STPCh. 5.8 - Prob. 42MRCh. 5.8 - Prob. 43MRCh. 5.8 - Prob. 44MRCh. 5.8 - Prob. 45MRCh. 5.8 - Prob. 46MRCh. 5.8 - Prob. 47MRCh. 5.8 - Prob. 1CBCh. 5.8 - Prob. 2CBCh. 5 - Prob. 1GRCh. 5 - Prob. 2GRCh. 5 - Prob. 3GRCh. 5 - Prob. 4GRCh. 5 - Prob. 5GRCh. 5 - Prob. 6GRCh. 5 - Prob. 7GRCh. 5 - Prob. 8GRCh. 5 - Prob. 9GRCh. 5 - Prob. 10GRCh. 5 - Prob. 11GRCh. 5 - Prob. 12GRCh. 5 - Prob. 13GRCh. 5 - Prob. 14GRCh. 5 - Prob. 15GRCh. 5 - Prob. 16GRCh. 5 - Prob. 17GRCh. 5 - Prob. 1CRCh. 5 - Prob. 2CRCh. 5 - Prob. 3CRCh. 5 - Prob. 4CRCh. 5 - Prob. 5CRCh. 5 - Prob. 6CRCh. 5 - Prob. 7CRCh. 5 - Prob. 8CRCh. 5 - Prob. 9CRCh. 5 - Prob. 10CRCh. 5 - Prob. 11CRCh. 5 - Prob. 12CRCh. 5 - Prob. 13CRCh. 5 - Prob. 14CRCh. 5 - Prob. 15CRCh. 5 - Prob. 16CRCh. 5 - Prob. 17CRCh. 5 - Prob. 18CRCh. 5 - Prob. 19CRCh. 5 - Prob. 20CRCh. 5 - Prob. 21CRCh. 5 - Prob. 22CRCh. 5 - Prob. 23CRCh. 5 - Prob. 24CRCh. 5 - Prob. 25CRCh. 5 - Prob. 26CRCh. 5 - Prob. 27CRCh. 5 - Prob. 28CRCh. 5 - Prob. 29CRCh. 5 - Prob. 30CRCh. 5 - Prob. 31CRCh. 5 - Prob. 32CRCh. 5 - Prob. 33CRCh. 5 - Prob. 34CRCh. 5 - Prob. 35CRCh. 5 - Prob. 36CRCh. 5 - Prob. 37CRCh. 5 - Prob. 38CRCh. 5 - Prob. 39CRCh. 5 - Prob. 40CRCh. 5 - Prob. 1CTCh. 5 - Prob. 2CTCh. 5 - Prob. 3CTCh. 5 - Prob. 4CTCh. 5 - Prob. 5CTCh. 5 - Prob. 6CTCh. 5 - Prob. 7CTCh. 5 - Prob. 8CTCh. 5 - Prob. 9CTCh. 5 - Prob. 10CTCh. 5 - Prob. 11CTCh. 5 - Prob. 12CTCh. 5 - Prob. 13CTCh. 5 - Prob. 14CTCh. 5 - Prob. 15CTCh. 5 - Prob. 16CTCh. 5 - Prob. 17CTCh. 5 - Prob. 18CTCh. 5 - Prob. 19CTCh. 5 - Prob. 20CTCh. 5 - Prob. 21CTCh. 5 - Prob. 22CTCh. 5 - Prob. 23CTCh. 5 - Prob. 1CCSRCh. 5 - Prob. 2CCSRCh. 5 - Prob. 3CCSRCh. 5 - Prob. 4CCSRCh. 5 - Prob. 5CCSRCh. 5 - Prob. 6CCSRCh. 5 - Prob. 7CCSRCh. 5 - Prob. 8CCSRCh. 5 - Prob. 9CCSRCh. 5 - Prob. 10CCSRCh. 5 - Prob. 11CCSRCh. 5 - Prob. 12CCSRCh. 5 - Prob. 13CCSRCh. 5 - Prob. 14CCSRCh. 5 - Prob. 15CCSRCh. 5 - Prob. 16CCSRCh. 5 - Prob. 17CCSRCh. 5 - Prob. 18CCSRCh. 5 - Prob. 19CCSRCh. 5 - Prob. 20CCSRCh. 5 - Prob. 21CCSRCh. 5 - Prob. 22CCSRCh. 5 - Prob. 23CCSRCh. 5 - Prob. 24CCSRCh. 5 - Prob. 25CCSRCh. 5 - Prob. 26CCSRCh. 5 - Prob. 27CCSRCh. 5 - Prob. 28CCSRCh. 5 - Prob. 29CCSRCh. 5 - Prob. 30CCSRCh. 5 - Prob. 31CCSRCh. 5 - Prob. 32CCSR

Additional Math Textbook Solutions

Find more solutions based on key concepts
Genetics. In Exercises 15–20, refer to the accompanying table, which describes results from groups of 8 births ...

Elementary Statistics (13th Edition)

In Problems 31-42: (a) Find the domain of each function. (b) Locate any intercepts. (c) Graph each function. (d...

Precalculus

the sum of the given numbers

Pre-Algebra Student Edition

Voting A random sample of likely voters showed that 49 planned to support Measure X. The margin of error is 3 p...

Introductory Statistics

Moving shadow A 5-foot-tall woman walks at 8 ft/s toward a streetlight that is 20 ft above the ground. What is ...

Calculus: Early Transcendentals (2nd Edition)

Write a sentence that illustrates the use of 78 in each of the following ways. a. As a division problem. b. As ...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Which is the best chart: Selecting among 14 types of charts Part II; Author: 365 Data Science;https://www.youtube.com/watch?v=qGaIB-bRn-A;License: Standard YouTube License, CC-BY