
Concept explainers
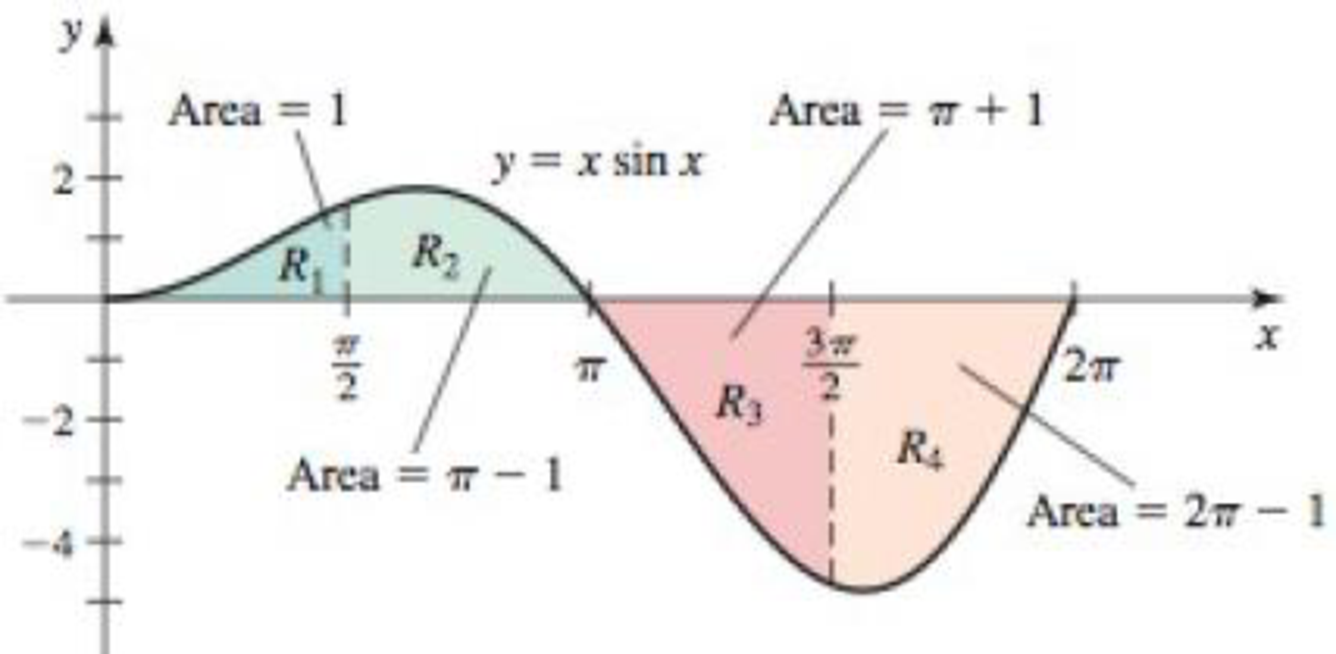
Net area from graphs The accompanying figure shows four regions bounded by the graph of y = x sin x: R1, R2, R3, and R4, whose areas are 1, π − 1, π + 1, and 2π − 1, respectively. (We verify these results later in the text.) Use this information to evaluate the following integrals.
38.
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Single Variable Calculus: Early Transcendentals (2nd Edition) - Standalone book
Additional Math Textbook Solutions
Elementary Statistics
Introductory Statistics
University Calculus: Early Transcendentals (4th Edition)
Pre-Algebra Student Edition
Elementary Statistics: Picturing the World (7th Edition)
A First Course in Probability (10th Edition)
- Find the point on the graph of the given function at which the slope of the tangent line is the given slope. 2 f(x)=8x²+4x-7; slope of the tangent line = -3arrow_forwardUse the product rule to find the derivative of the following. p(y) (y¹ + y²) (6y¯³-10y¯4)arrow_forwardplease dont use chat gptarrow_forward
- Find this expression in frequency domain in a expression y(t), in time, that is.arrow_forwardplease dont use chat gptarrow_forwardQuestion Given the graph of f(z) below, find the graph of the derivative of f(z). Select the correct answer below: ° 7-6-5-4-3 123 ° ° 2 -7-6-5-4-3- 123 -° 2-4 -°- °- -7-6-5-4-3-2-1 1 5 +arrow_forward
- Which of the functions shown below is differentiable at = 0? Select the correct answer below: -7-6-5-4- -6-5-4-3-21, -7-6-5-4-3-2 -7-6-5-4-3-2-1 2 4 5 6 -1arrow_forwardcorrect answer is Acould you please show me how to compute using the residue theoremarrow_forwardthe correct answer is A please explainarrow_forward
 Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
