Chapter 5.2, Problem 39E

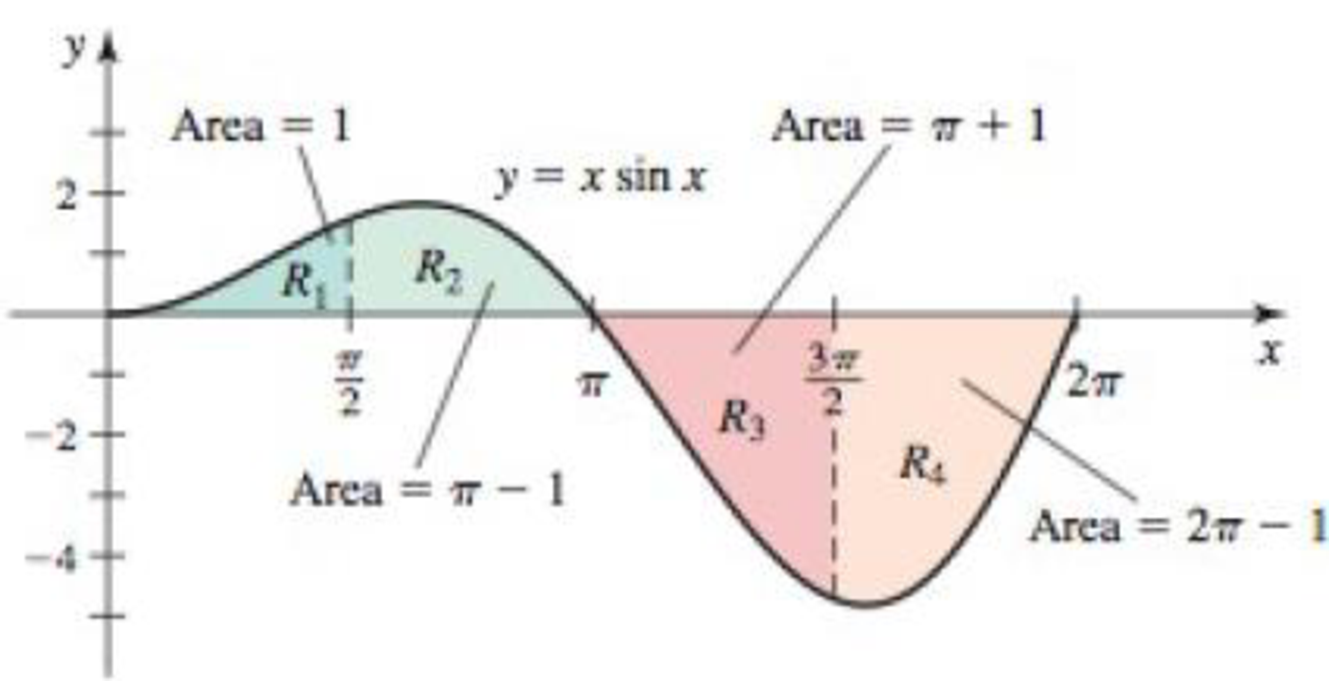
Net area from graphs The accompanying figure shows four regions bounded by the graph of y = x sin x: R₁, R₂, R₃, and R₄, whose areas are 1, π − 1, π + 1, and 2π − 1, respectively. (We verify these results later in the text.) Use this information to evaluate the following integrals.

39. ${\displaystyle {\int }_0^{2\pi }x\sin xdx}$