Chapter 5, Problem 59RE

(a)

To determine

To Find: The domain of the $f$ .

Answer to Problem 59RE

The domain of the function is $\left(-\infty ,\infty \right)$ .

Explanation of Solution

Given:

The given function is $f\left(x\right)=1-e^{-x}$ .

Calculation:

Consider the given function is,

  $f\left(x\right)=1-e^{-x}$

The function is defined for all the value of $x$ , thus the domain of the function is $f\left(x\right)=\left(-\infty ,\infty \right)$ .

(b)

To determine

To Find: The graph for the function $f$ .

Explanation of Solution

Given:

The given function is $f\left(x\right)=1-e^{-x}$ .

Calculation:

The graph for the given function is shown in Figure 1

  

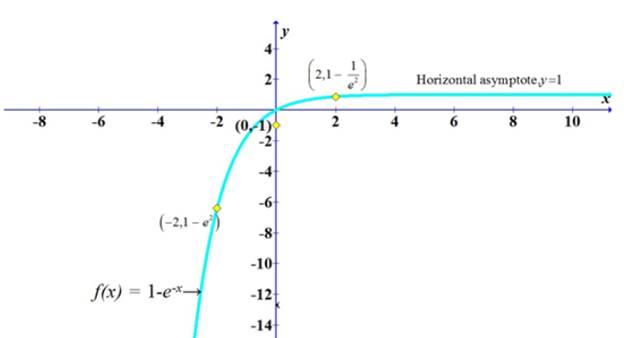
Figure 1

(c)

To determine

To Find: The range and the asymptote of the graph.

Answer to Problem 59RE

The range of the function is, $\left(-\infty ,\infty \right)$ and the horizontal asymptotes of the given function is $y=1$ .

Explanation of Solution

Given:

The given function is $f\left(x\right)=1-e^{-x}$ .

Calculation:

Consider the given function,

  $f\left(x\right)=1-e^{-x}$

The range of the above function is the set of all the real numbers that is,

  $\left(-\infty ,\infty \right)$

Thus, the horizontalasymptotes of the given function is,

  $y=1$

(d)

To determine

To Find: The function $f^{-1}$ .

Answer to Problem 59RE

The inverse of the functions is $-\ln \left(1-x\right)$ .

Explanation of Solution

Given:

The given function is $f\left(x\right)=1-e^{-x}$ .

Calculation:

Consider the given function,

  $f\left(x\right)=1-e^{-x}$

Then,

  $y=1-e^{-x}$

Then, the inverse of the function is,

  $\begin{array}{l}x=1-e^{-y}\\ e^{-y}=1-x\end{array}$

Take the log of both the sides and solve as,

  $\begin{array}{l}\ln e^{-y}=\ln \left(1-x\right)\\ y=-\ln \left(1-x\right)\end{array}$

(e)

To determine

To Find: The range of the function.

Answer to Problem 59RE

The range of the function is $\left(-\infty ,\infty \right)$ .

Explanation of Solution

Given:

The given function is $f\left(x\right)=1-e^{-x}$ .

Calculation:

Consider the given function,

  $f\left(x\right)=1-e^{-x}$

The domain of the function $f\left(x^{-1}\right)$ is equal to the range of the $f\left(x\right)$ that is the set of all the real number $\left(-\infty ,\infty \right)$ and the range of the inverse function is the domain of the original function that is $\left(-\infty ,\infty \right)$ in the interval notation.

(f)

To determine

To Find: The graph of the function $f^{-1}$ .

Explanation of Solution

Given:

The inverse of the function is $-\ln \left(1-x\right)$ .

Calculation:

The graph for the inverse of the function is shown in Figure 2

  

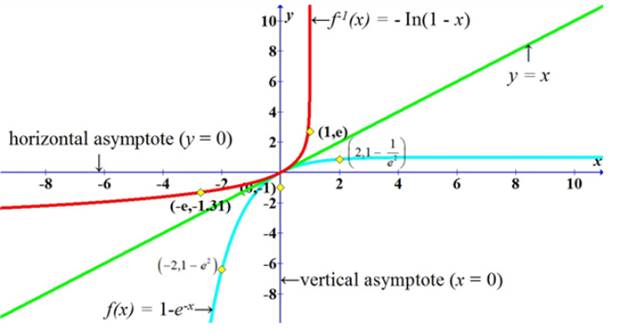
Figure 2