To determine To find: a. If E = 120 volts, R = 10 ohms and L = 5 henrys, how much current I 1 is flowing after 0.3 second? After 0.5 second? After 1 second? Answer a. 5.4143 current I 1 is flowing after 0.3 second, 7.5855 current I 1 is flowing after 0.5 second, 10.3760 current I 1 is flowing after 1 second. Explanation Given: I = E R [ 1 − e − ( R L ) t ] Calculation: a. E = 120 , R = 10 and L = 5 How much current I 1 is flowing after 0.3 second = 120 10 [ 1 − e − ( 10 5 ) 0.3 ] = 12 [ 1 − 0.5488 ] = 12 [ 0.4512 ] = 5.4143 How much current I 1 is flowing after 0.5 second = 120 10 [ 1 − e − ( 10 5 ) 0.5 ] = 12 [ 1 − 0.3679 ] = 12 [ 0.6321 ] = 7.5855 How much current I 1 is flowing after 1 second = 120 10 [ 1 − e − ( 10 5 ) 1 ] = 12 [ 1 − 0.1353 ] = 12 [ 0.8647 ] = 10.3760 To determine To find: b. The maximum current. Answer b. 12 maximum current when time approaches infinity. Explanation Given: I = E R [ 1 − e − ( R L ) t ] Calculation: b. We obtain maximum current when time approaches infinity = 120 10 [ 1 − e − ( 10 5 ) ∞ ] = 12 [ 1 − e − ∞ ] = 12 [ 1 − 0 ] = 12 To determine To find: c. Graph the function I = I 1 ( t ) , measuring I along the y -axis and t along the x -axis . Answer c. Explanation Given: I = E R [ 1 − e − ( R L ) t ] Calculation: c. To determine To find: d. If E = 120 volts, R = 5 ohms, and L = 10 henrys, how much current I 2 is flowing after 0.3 second? After 0.5 second? After 1 second? Answer d. 3.3430 current I 2 is flowing after 0.3 second, 5.3088 current I 2 is flowing after 0.5 second, 9.4433 current I 2 is flowing after 1 second, Explanation Given: I = E R [ 1 − e − ( R L ) t ] Calculation: d. E = 120 , R = 5 and L = 10 How much current I 2 is flowing after 0.3 second = 120 5 [ 1 − e − ( 5 10 ) 0.3 ] = 24 [ 1 − 0.8607 ] = 24 [ 0.1393 ] = 3.3430 How much current I 2 is flowing after 0.5 second = 120 5 [ 1 − e − ( 5 10 ) 0.5 ] = 24 [ 1 − 0.7788 ] = 2 [ 0.2212 ] = 5.3088 How much current I 2 is flowing after 1 second = 120 5 [ 1 − e − ( 5 10 ) 1 ] = 24 [ 1 − 0.6065 ] = 24 [ 0.3935 ] = 9.4433 To determine To find: e. The maximum current. Answer e. 24 maximum current when time approaches infinity. Explanation Given: I = E R [ 1 − e − ( R L ) t ] Calculation: e. We obtain maximum current when time approaches infinity. = 120 5 [ 1 − e − ( 5 10 ) ∞ ] = 24 [ 1 − e − ∞ ] = 24 [ 1 − 0 ] = 24 To determine To find: f. Graph the function I = I 2 ( t ) , measuring I along the y -axis and t along the x -axis . Answer f. Explanation Given: I = E R [ 1 − e − ( R L ) t ] Calculation: f.

9th Edition

ISBN: 9780321716835

Author: Michael Sullivan

Publisher: Addison Wesley

See similar textbooks

Concept explainers

Differential Equations

Have you ever observed the movement of the satellites and rockets or how the planets go around the sun in their orbits? How will you determine their motion? Definitely they follow some scientific laws and these kinds of problems are framed as differentia…

Videos

Textbook Question

Chapter 5.3, Problem 113AYU

119. Current in an RL Circuit The equation governing the amount of current I (in amperes) after time t (in seconds) in a single RL circuit consisting of a resistance R (in ohms), an inductance L (in henrys), and an electromotive force E (in voles) is

$I = \frac{E}{R} [1 - e^{- (R / L) t}]$

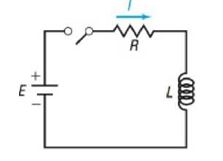
Chapter 5.3, Problem 113AYU, 119. Current in an RL Circuit The equation governing the amount of current I (in amperes) after time

(a) If $E = 120$ volts, $R = 10$ ohms, and $L = 5$ henrys, how much current I₁ is flowing after 0.3 second? After 0.5 second? After 1 second?

(b) What is the maximum current?

(d) If $E = 120$ volts, $R = 5$ ohms, and $L = 10$ henrys, how much current I₂ is flowing after 0.3 second? After 0.5 second? After 1 second?

(e) What is the maximum current?

(f) Graph the function $I = I_{2} (t)$ on the same coordinate axes as $I_{1} (t)$ .

Expert Solution

To determine

To find:

a. If $E = 120$ volts, $R = 10$ ohms and $L = 5$ henrys, how much current $I_{1}$ is flowing after $0.3$ second? After $0.5$ second? After 1 second?

Answer to Problem 113AYU

a. $5.4143$ current $I_{1}$ is flowing after $0.3$ second, $7.5855$ current $I_{1}$ is flowing after $0.5$ second, $10.3760$ current $I_{1}$ is flowing after 1 second.

Explanation of Solution

Given:

$I = \frac{E}{R} [1 - e^{- (\frac{R}{L}) t}]$

Calculation:

a. $E = 120, R = 10$ and $L = 5$

How much current $I_{1}$ is flowing after $0.3$ second $= \frac{120}{10} [1 - e^{- (\frac{10}{5}) 0.3}]$

$= 12 [1 - 0.5488]$

$= 12 [0.4512]$

$= 5.4143$

How much current $I_{1}$ is flowing after $0.5$ second $= \frac{120}{10} [1 - e^{- (\frac{10}{5}) 0.5}]$

$= 12 [1 - 0.3679]$

$= 12 [0.6321]$

$= 7.5855$

How much current $I_{1}$ is flowing after 1 second $= \frac{120}{10} [1 - e^{- (\frac{10}{5}) 1}]$

$= 12 [1 - 0.1353]$

$= 12 [0.8647]$

$= 10.3760$

Expert Solution

To determine

To find:

b. The maximum current.

Answer to Problem 113AYU

b. 12 maximum current when time approaches infinity.

Explanation of Solution

Given:

$I = \frac{E}{R} [1 - e^{- (\frac{R}{L}) t}]$

Calculation:

b. We obtain maximum current when time approaches infinity

$= \frac{120}{10} [1 - e^{- (\frac{10}{5}) \infty}]$

$= 12 [1 - e^{- \infty}]$

$= 12 [1 - 0]$

$= 12$

Expert Solution

To determine

To find:

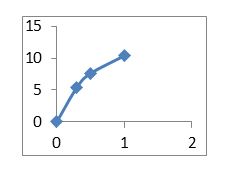
c. Graph the function $I = I_{1} (t),$ measuring $I$ along the $y -axis$ and $t$ along the $x -axis$ .

Answer to Problem 113AYU

Precalculus, Chapter 5.3, Problem 113AYU , additional homework tip 1

Explanation of Solution

Given:

$I = \frac{E}{R} [1 - e^{- (\frac{R}{L}) t}]$

Calculation:

Precalculus, Chapter 5.3, Problem 113AYU , additional homework tip 2

Expert Solution

To determine

To find:

d. If $E = 120$ volts, $R = 5$ ohms, and $L = 10$ henrys, how much current $I_{2}$ is flowing after $0.3$ second? After $0.5$ second? After 1 second?

Answer to Problem 113AYU

d. $3.3430$ current $I_{2}$ is flowing after $0.3$ second, $5.3088$ current $I_{2}$ is flowing after $0.5$ second, $9.4433$ current $I_{2}$ is flowing after 1 second,

Explanation of Solution

Given:

$I = \frac{E}{R} [1 - e^{- (\frac{R}{L}) t}]$

Calculation:

d. $E = 120, R = 5$ and $L = 10$

How much current $I_{2}$ is flowing after $0.3$ second $= \frac{120}{5} [1 - e^{- (\frac{5}{10}) 0.3}]$

$= 24 [1 - 0.8607]$

$= 24 [0.1393]$

$= 3.3430$

How much current $I_{2}$ is flowing after $0.5$ second $= \frac{120}{5} [1 - e^{- (\frac{5}{10}) 0.5}]$

$= 24 [1 - 0.7788]$

$= 2 [0.2212]$

$= 5.3088$

How much current $I_{2}$ is flowing after 1 second $= \frac{120}{5} [1 - e^{- (\frac{5}{10}) 1}]$

$= 24 [1 - 0.6065]$

$= 24 [0.3935]$

$= 9.4433$

Expert Solution

To determine

To find:

e. The maximum current.

Answer to Problem 113AYU

e. 24 maximum current when time approaches infinity.

Explanation of Solution

Given:

$I = \frac{E}{R} [1 - e^{- (\frac{R}{L}) t}]$

Calculation:

e. We obtain maximum current when time approaches infinity.

$= \frac{120}{5} [1 - e^{- (\frac{5}{10}) \infty}]$

$= 24 [1 - e^{- \infty}]$

$= 24 [1 - 0]$

$= 24$

Expert Solution

To determine

To find:

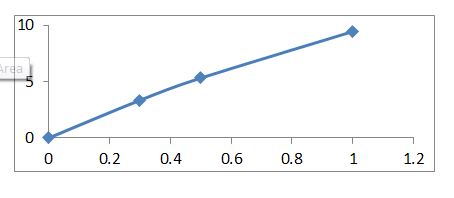
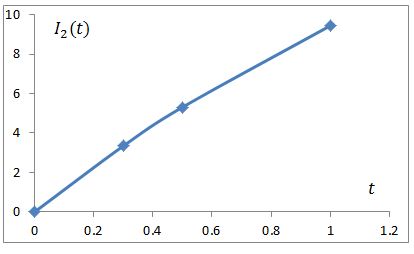
f. Graph the function $I = I_{2} (t),$ measuring $I$ along the $y -axis$ and $t$ along the $x -axis$ .

Answer to Problem 113AYU

Precalculus, Chapter 5.3, Problem 113AYU , additional homework tip 3

Explanation of Solution

Given:

$I = \frac{E}{R} [1 - e^{- (\frac{R}{L}) t}]$

Calculation:

Precalculus, Chapter 5.3, Problem 113AYU , additional homework tip 4

Chapter 5.3, Problem 112AYU

Chapter 5.3, Problem 114AYU

Chapter 5 Solutions

Precalculus

Ch. 5.1 - Find f( 3 ) if f( x )=4 x 2 +5x . (pp. 60-62)Ch. 5.1 - Find f(3x) if f(x)=42 x 2 . (pp. 60-62)Ch. 5.1 - Find the domain of the function f(x)= x 2 1 x 2 25...Ch. 5.1 - Prob. 4AYU Ch. 5.1 - Prob. 5AYU Ch. 5.1 - Prob. 6AYU Ch. 5.1 - In Problems 9 and 10, evaluate each expression...Ch. 5.1 - In Problems 9 and 10, evaluate each expression...Ch. 5.1 - In Problems 11 and 12, evaluate each expression...Ch. 5.1 - In Problems 11 and 12, evaluate each expression...

Additional Math Textbook Solutions

Find more solutions based on key concepts

A categorical variable has three categories, with the following frequencies of occurrence: a. Compute the perce...

Basic Business Statistics, Student Value Edition

Symmetry in graphs State whether the functions represented by graphs A, B, and C in the figure are even, odd, o...

Calculus: Early Transcendentals (2nd Edition)

Student Ages The mean age of all 2550 students at a small college is 22.8 years with a standard deviation is 3....

Introductory Statistics

Identify f as being linear, quadratic, or neither. If f is quadratic, identify the leading coefficient a and ...

College Algebra with Modeling & Visualization (5th Edition)

the slope of the line

Pre-Algebra Student Edition

3. For the same sample statistics, which level of confidence would produce the widest confidence interval? Expl...

Elementary Statistics: Picturing the World (7th Edition)

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.