Elementary Principles Of Chemical Processes
4th Edition
ISBN: 9781119254003
Author: Richard M. Felder And Ronald W. Rousseau
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5, Problem 5.42P
Fermentation is a biochemical process in which a carbohydrate—such as the sugar glucose—is converted by bacteria or yeast to an organic compound—such as ethanol—and carbon dioxide. The process is best known for its use in making beer_ wine, and other alcoholic beverages, but it is also used to produce a wide range of other industrially important chemicals.
The diagram below shows a continuous fermentation process. An aqueous solid-liquid slurry containing a carbohydrate and bacteria enters a stirred tank where it undergoes fermentation. Fermentation products, including species condensed from the off-gas, and bacteria are withdrawn from the tank. A mixer with multiple rotating impellers keeps the solids in the tank suspended in the liquid. An air stream enters the fermenter through a sparger (something like an inverted shower head) designed to produce small bubbles that rise through the mixture and remove the CO2 formed in the reaction. Some of the oxygen in the air fed to the fermenter is consumed by the bacteria. The gas products go through a condenser, which condenses most of the water and returns it to the fermenter, and the uncondensed off-gas goes to a dryer and then to a mass spectrometer, where its composition is determined. The ?ow rate of the air feed is measured to be 0.600 SLPM (liters per minute at standard temperature and pressure) and the measured compositions of the air and the off- gas are shown on the diagram. The off-gas is at 28°C and 1.1 atm.
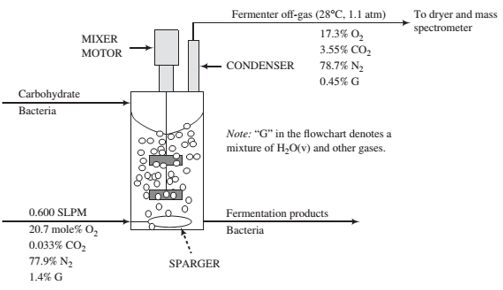
(a) Describe in your own words the purpose of this process and the functions of the mixer, the air, and the sparger.
(b) In a small laboratory fermenter, the mass of the broth in the tank is 0.58 kg, and the broth density is 1.05 kg/L. Calculate the carbon dioxide evolution rate (CER) and the oxygen uptake rate (OUR) in mmol/(h ( L), where the volume unit in the denominator refers to the volume of broth in the tank. Also, calculate the off-gas volumetric ?ow rate in L/min.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
⑤
b
Δε
m
ab
C
40
Problem 10.16 An isosceles triangle of base 40 mm and altitude 54 mm has its base in the V.P. The
surface of the plane is inclined at 50° to the V.P. and perpendicular to the H.P. Draw its projections.
Construction Refer to Fig. 10.17.
An isosceles triangle has its base in the V.P., so con-
sider that initially the triangle ABC is placed in the
V.P. with base AB perpendicular to the H.P.
1. First stage Draw a triangle a'b'c' keeping
a'b' perpendicular to xy to represent the front
view. Project the corners to xy and obtain ac
as the top view.
2. Second stage Reproduce the top view of first
stage keeping ab on xy and ac inclined at 50°
to xy. Obtain new points a', b' and c' in the
front view by joining the points of intersection
of the vertical projectors from a, b and c of the
second stage with the corresponding horizontal
locus lines from a', b' and c' of the first stage.
Join a'b'c' to represent the final front view.
Here, the front view is an equilateral triangle
of side 40 mm.
X
54…
%9..+
۱:۱۹
X
خطأ
عذرا ، الرقم الذي أدخلته خاطئ. يرجى إدخال رقم
بطاقة الشحن الصالحة والمحاولة مرة أخرى.
رصيد هاتفك
قم بمسح الرمز
=
رقم بطاقة التعبئة
7794839909080
رمز مكون من 13 او 14 رقماً
طريقة إعادة التعبئة
قم باعادة تعبئة الرصيد
إعادة تعبئة الإنترنت
إعادة تعبئة الرصيد
O
>
Chapter 5 Solutions
Elementary Principles Of Chemical Processes
Ch. 5 - A liquid mixture containing 40.0 wt% n-octane and...Ch. 5 - Prob. 5.2PCh. 5 - Prob. 5.3PCh. 5 - Prob. 5.4PCh. 5 - Prob. 5.5PCh. 5 - Prob. 5.6PCh. 5 - Prob. 5.7PCh. 5 - Prob. 5.8PCh. 5 - Prob. 5.9PCh. 5 - Prob. 5.10P
Ch. 5 - Prob. 5.11PCh. 5 - Prob. 5.12PCh. 5 - Prob. 5.13PCh. 5 - Prob. 5.14PCh. 5 - Prob. 5.15PCh. 5 - Prob. 5.16PCh. 5 - Prob. 5.17PCh. 5 - Prob. 5.18PCh. 5 - Prob. 5.19PCh. 5 - A device has been designed to measure the flow...Ch. 5 - Prob. 5.21PCh. 5 - Prob. 5.22PCh. 5 - Spray drying is a process in which a liquid...Ch. 5 - Prob. 5.24PCh. 5 - Lewis12 describes the hazards of breathing air...Ch. 5 - A stream of air at 35°C and a gauge pressure of...Ch. 5 - Prob. 5.27PCh. 5 - In froth ?otation, air is bubbled through an...Ch. 5 - Prob. 5.29PCh. 5 - Prob. 5.30PCh. 5 - Bread is typically made by ?rst dissolving...Ch. 5 - Prob. 5.32PCh. 5 - Prob. 5.33PCh. 5 - Prob. 5.34PCh. 5 - Prob. 5.35PCh. 5 - Prob. 5.36PCh. 5 - Prob. 5.37PCh. 5 - Prob. 5.38PCh. 5 - Prob. 5.39PCh. 5 - A spray-drying operation similar to that described...Ch. 5 - Prob. 5.41PCh. 5 - Fermentation is a biochemical process in which a...Ch. 5 - Prob. 5.43PCh. 5 - Prob. 5.44PCh. 5 - Ethane at 25°C and 1.1 atm (abs) flowing at a rate...Ch. 5 - The ?ow of air to a gas-?red boiler furnace is...Ch. 5 - Prob. 5.47PCh. 5 - The oxidation of nitric oxide NO+12O2NO2 takes...Ch. 5 - Prob. 5.49PCh. 5 - 5.50.19 In chemical vapor deposition (CVD), a...Ch. 5 - A gas turbine power plant receives a shipment of...Ch. 5 - Prob. 5.52PCh. 5 - 5.53.20 Chemicals are stored in a laboratory with...Ch. 5 - Prob. 5.54PCh. 5 - Prob. 5.55PCh. 5 - A stream of ho dry nitrogen flows through a...Ch. 5 - Prob. 5.57PCh. 5 - You have purchased a gas cylinder that is supposed...Ch. 5 - The current global reliance on fossil fuels for...Ch. 5 - Two humid gas streams are combined in a heated...Ch. 5 - Most of the concrete used in the construction of...Ch. 5 - The ultimate analysis of a No. 4 fuel oil is 86.47...Ch. 5 - A stream of liquid n-pentane flows at a rate of...Ch. 5 - Alka-Seltzer( is an over-the-counter medicine used...Ch. 5 - Hydrogen sul?de has the distinctive unpleasant...Ch. 5 - The quantity of sulfuric acid used globally places...Ch. 5 - A small power plant produces 500 MW of electricity...Ch. 5 - You have been assigned the task of measuring the...Ch. 5 - Prob. 5.69PCh. 5 - Methanol is synthesized from carbon monoxide and...Ch. 5 - Prob. 5.71PCh. 5 - Prob. 5.72PCh. 5 - Steam reforming is an important technology for...Ch. 5 - A ?owchart of a methanol synthesis process is...Ch. 5 - The measured volumetric flow rate of ethane at...Ch. 5 - Prob. 5.76PCh. 5 - Methanol is to be delivered to a process unit at a...Ch. 5 - Prob. 5.78PCh. 5 - Prob. 5.79PCh. 5 - Prob. 5.80PCh. 5 - Prob. 5.81PCh. 5 - Prob. 5.82PCh. 5 - Prob. 5.83PCh. 5 - Prob. 5.84PCh. 5 - Prob. 5.85PCh. 5 - Prob. 5.86PCh. 5 - Prob. 5.87PCh. 5 - Prob. 5.88PCh. 5 - Prob. 5.89PCh. 5 - A fuel cell is an electrochemical device that...Ch. 5 - In a metered-dose inhaler (MDI), such as those...Ch. 5 - Prob. 5.92PCh. 5 - Prob. 5.93PCh. 5 - Approximately 150 SCFM (standard cubic feet per...Ch. 5 - Prob. 5.95PCh. 5 - Prob. 5.96PCh. 5 - Prob. 5.97PCh. 5 - The product gas from a coal gasification plant...Ch. 5 - Prob. 5.99PCh. 5 - Prob. 5.100PCh. 5 - A gas mixture consisting of 15.0 mole% methane....Ch. 5 - A system has been devised to store acetonitrile...Ch. 5 - Prob. 5.103PCh. 5 - Prob. 5.104P
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
What is a recursive algorithms base case? What is the recursive case?
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
What factors tend to cause a drill to drift off the centerline of a hole?
Degarmo's Materials And Processes In Manufacturing
What is array bounds checking? Does C++ perform it?
Starting Out with C++: Early Objects (9th Edition)
a. What single instruction in the Vole machine language could be used to accomplish a 5-bit right circular shif...
Computer Science: An Overview (13th Edition) (What's New in Computer Science)
Use the following tables for your answers to questions 3.7 through 3.51 : PET_OWNER (OwnerID, OwnerLasst Name, ...
Database Concepts (8th Edition)
Explain what happens when a Java program attempts to divide one integer by another. What happens to the fractio...
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Problem 10.14 A hexagonal plane of side 30 mm has a corner in the V.P. The surface of the plane is inclined at 45° to the V.P. and perpendicular to the H.P. Draw its projections. Assume that the diagonal through the corner in the V.P. is parallel to the H.P. d' a 2 b b.f C' c.e b 'C' H.P. (a) V.P E HEX 30 e' O' d' a a' b' C' b' X y a b,f c,e d b,f (b) c,earrow_forwardProblem 10.18 A 60° set-square has the shortest edge of 40 mm lying in the V.P. The surface is in- clined to the V.P. and perpendicular to the H.P. such that the front view appears as an isosceles triangle. Draw the projections of the set-square and determine its inclination with the V.P. Construction Refer to Fig. 10.18. A 60° set-square inclined to the V.P. and per- pendicular to the H.P. can appear as an isosceles triangle in the front view, when the shorter edge is in the V.P. 1. First stage Draw a right angled triangle 40 a' a' b' c' b' X 40 C' a,b C a,b a'b'c' keeping 40 mm long a'b' perpen- dicular to xy. Project the corners to xy and obtain ac as the top view. 2. Second stage Draw another right angled triangle a'b'c' on the horizontal locus line from points a', b' and c' of the first stage such that length of b'c' is equal to that of a'b'. Project a'b' to meet xy at ab. Draw an arc with centre a and radius equal to ac of the first stage to meet the vertical projector of c' at…arrow_forward□ 40 a' 12 o' a O d'arrow_forwardTL = 85 D. Problem 9.12 The top view of a line measures 60 mm. The line is parallel to the V.P. and inclined at 45° to the H.P. One end of the line is 25 mm in front of the V.P. and lies on the H.P. Draw its projections and determine the true length. Interpretation Let the line be PQ parallel to the V.P. The front view has true length and the top view is parallel to xy. Construction Refer to Fig. 9.12. 1. Draw a reference line xy. Mark point p' on xy and point p 25 mm below xy. 2. Draw a 60 mm long line pq parallel to xy. This repre- sents the top view. 3. Draw line from point p', inclined at 45° to xy to meet the projector from point q at point q'. Join p'a' to represent the front view. Measure length of p'a' as true length of line PQ. Here T.L. = 85 mm. Result True length of line PQ is p'q' = 85 mm. 5 Fig. 9.12 p 60 σarrow_forwardProblem 9.13 A 70 mm long line PQ does not have H.T. and V.T. One end of the line is 30 mm in front of the V.P. and 20 mm above the H.P. Draw its projections. Interpretation As the line PQ does not have H.T. and V.T., it is parallel to both H.P. and V.P. Construction Refer to Fig. 9.13. 1. Draw a reference line xy. Mark point p' 20 mm above xy and point p 30 mm below xy. 2. Draw a 70 mm long line p'a' parallel to xy to repre- sent the front view. X 20 p Fig. 9.13 3. Also, draw a 70 mm long line pq parallel to xy to represent the top view. 70 q yarrow_forwardProblem 10.19 A square lamina ABCD of side 40 mm is suspended from a point O such that its surface is inclined at 30° to the V.P. The point O lies on the side AB 12 mm away from A. Draw its projections. Construction Refer to Fig. 10.19. 1. First stage Draw a square a'b'c'd keeping a'd' parallel to xy. Mark a point o' on a'ď at a distance 12 mm from end a' as the point of suspension. Also, mark the centre of the square g' to represent the centre of gravity. 2. Second stage Reproduce the front view of first stage such that o'g' is perpendicular to xy. Project corners and obtain bd as the top view. 3. Third stage Reproduce the top view keeping bd inclined at 30° to xy. Obtain new points a', b', c' and ď' in the front view by joining the points of intersection of the vertical projectors drawn from points a, b, c and d of the third stage with the corresponding horizontal locus lines drawn from points a', b', c' and ď of the second stage. Join new a'b'c'd to represent the final front view.arrow_forwardProblem 10.15 A circular plane of diameter 50 mm is resting on a point of the circumference on the V.P. The plane is inclined at 30° to the V.P. and the centre is 35 mm above the H.P. Draw its projections.arrow_forwardYou are asked to manufacture 10 kg of polyester with a number-average molecular weight of 1000 by polymerizing butane-1,4-diol(HO(CH2)4OH) with adipic acid (HOOC-(CH2)4-COOH).a) What weight of diol and diacid do you need, respectively? To whatextent, p, should the reaction be carried out to? Assume a stoichiometricbalance.b) What are the number and weight fractions of dimer, trimer and tetramerat this point in the reaction?c) Because of the polymerization by dehydration to olefin, 3 mol% of thediol will be lost. What would be the number-average molecular weightwhen the reaction is carried out to the same extent? How could you offsetthis loss so that the desired molecular weightarrow_forward9.4. A PID temperature controller is at steady state with an output pressure of 9 psig. The set point and process temperature are initially the same. At time = 0, the set point is increased at the rate of 0.5°F/min. The motion of the set point is in the direction of lower temperatures. If the current settings are PART 3 LINEAR CLOSED-LOOP SYSTEMS Ke = 2 psig/°F Ti = 1.25 min TD = 0.4 min plot the output pressure versus time.arrow_forward9.6. A PI controller has the transfer function Determine the values of K, and T. 5s + 10 Ge Sarrow_forward9.5. The input & to a PI controller is shown in Fig. P9-5. Plot the output of the controller if Ke 2 and 0.50 min. - E 0.5 0 -0.5 0 FIGURE P9-5 2 4 t, minarrow_forward9.3. An ideal PD controller has the transfer function P Ke (TDs + 1) E An actual PD controller had the transfer function P = Ke E TDS +1 (TDIẞ)s +1 where ẞis a large constant in an industrial controller. If a unit-step change in error is introduced into a controller having the second transfer function, show that P(1) = Kc (1 + Ae˜¯BD) where A is a function of ẞwhich you are to determine. For ẞ=5 and K = 0.5, plot P(t) versus tl tp. As ẞ, show that the unit-step response approaches that for the ideal controller.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Introduction to Chemical Engineering Thermodynami...
Chemical Engineering
ISBN:9781259696527
Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:McGraw-Hill Education
Elementary Principles of Chemical Processes, Bind...
Chemical Engineering
ISBN:9781118431221
Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:WILEY
Elements of Chemical Reaction Engineering (5th Ed...
Chemical Engineering
ISBN:9780133887518
Author:H. Scott Fogler
Publisher:Prentice Hall
Industrial Plastics: Theory and Applications
Chemical Engineering
ISBN:9781285061238
Author:Lokensgard, Erik
Publisher:Delmar Cengage Learning
Unit Operations of Chemical Engineering
Chemical Engineering
ISBN:9780072848236
Author:Warren McCabe, Julian C. Smith, Peter Harriott
Publisher:McGraw-Hill Companies, The
Mod-01 Lec-23 Degrees of freedom analysis; Author: nptelhrd;https://www.youtube.com/watch?v=c4h85JjrkzQ;License: Standard YouTube License, CC-BY
Introduction to Degrees of Freedom; Author: LearnChemE;https://www.youtube.com/watch?v=tW1ft4y5fQY;License: Standard Youtube License