Chapter 5, Problem 5.11.11P

The three beams shown have approximately the same cross-sectional area. Beam 1 is a W 14 X 82 with flange plates; beam 2 consists of a web plate with four angles; and beam 3 is constructed of 2 C shapes with flange plates.

1. Which design has the largest moment capacity?
2. Which has the largest shear capacity?
3. Which is the most economical in bending?
4. Which is the most economical in shear?

Assume allowable stress values are: = 18 ksi and r_a=11 ksi. The most economical beam is that having the largest capacity-to-weight ratio. Neglect fabrication costs in answering parts (c) and (d) above. Note: Obtain the dimensions and properties of all rolled shapes from tables in Appendix F.

  

To determine

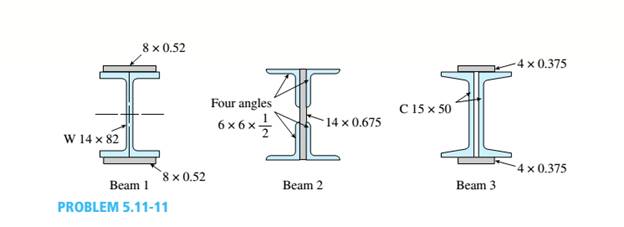
The beam of the largest momentum capacity.

Answer to Problem 5.11.11P

The beam of the largest momentum capacity is beam-1.

Explanation of Solution

Given information:

The allowable normal stress is $18\text{ksi}$ and the allowable shear stress is $11\text{ksi}$ .

Write the expression for the total moment of inertia of the beam-1.

  $I_1={\left(I_w\right)}_1+2\left[\frac{b_1{t}_1^3}{12}+b_1{t}_1{\left(\frac{{\left(h_w\right)}_1}{2}+\frac{t_1}{2}\right)}^2\right]$   ......(I)

Here, the total moment of inertia of the beam-1.is $I_1$ , moment of inertia of the web-1 is ${\left(I_w\right)}_1$ , height of the web-1 is ${\left(h_w\right)}_1$ , thickness of the cover plate is $t_1$ , and width of the cover plate is $b_1$ .

Write the expression for the total height of the beam-1.

  $h_1={\left(h_w\right)}_1+2t_1$   ......(II)

Here, the total height of the beam-1 is $h_1$ .

Write the expression for the total area of the beam-1.

  $A_1={\left(A_w\right)}_1+2b_1{t}_1$   ......(III)

Here, the total area of the beam-1.is $A_1$ and area of the web-1 is ${\left(A_w\right)}_1$

Write the expression for the section of the modulus of the beam-1.

  $S_1=\frac{2I_1}{h_1}$   ......(IV)

Here, the section of the modulus of the beam-1 $S_1$ .

Write the expression for the total moment of inertia of the beam-2.

  $I_2=\frac{b_2{t}_2^3}{12}+4\left[I_a+A_a{\left(\frac{h_2}{2}-C_a\right)}^2\right]$   ......(V)

Here, the total moment of inertia of the beam-2 is $I_2$ , width of the plate is $b_2$ , thickness of the plate is $t_2$ , moment of the inertia of the angle is $I_a$ , area of the angle is $A_a$ , height of the plate is $h_2$ , and centroid of the angle is $C_a$ .

Write the expression for the total area of the beam-2.

  $A_2=4A_a+b_2{t}_2$   ......(VI)

Here, the total area of the beam-2 is $A_2$ .

Write the expression for the section of the modulus of the beam-2.

  $S_2=\frac{2I_2}{h_2}$   ......(VII)

Here, the section of the modulus of the beam-2 is $S_2$ .

Write the expression for the total height of beam-3.

  $h_3=h_c+2t_3$   ......(VIII)

Here, the total height of beam-3 is $h_3$ , height of the channel is $h_c$ , thickness of the flange plate is $t_3$ .

Write the expression for the total moment of inertia of the beam-3.

  $I_3=2I_c+2\left[\frac{b_3{t}_3^3}{12}+b_3{t}_3{\left(\frac{h}{2}+\frac{t_3}{2}\right)}^2\right]$   ......(IX)

Here, the total moment of inertia of the beam-2 is $I_3$ , width of the flange plate is $b_3$ , moment of the inertia of the channel is $I_c$ .

Write the expression for the total area of the beam-3.

  $A_3=4A_c+2b_3{t}_3$   ......(X)

Here, the total area of the beam-3 is $A_3$ .

Write the expression for the section of the modulus of the beam-3.

  $S_3=\frac{2I_3}{h_3}$   ......(XI)

Here, the section of the modulus of the beam-3 $S_2$ .

Calculation:

Refer Table-F-1(a) “Properties of wide flange section” to obtain ${\left(A_w\right)}_1$ as $24\text{in}$ , ${\left(I_w\right)}_1$ as $881{\text{in}}^4$ , $b_1$ as $8\text{in}$ , $t_1$ as $0.52\text{in}$ , $t_{f1}$ as $0.855\text{in}$ , $b_{f1}$ as $10.1\text{in}$ .

Substitute $881{\text{in}}^4$ for ${\left(I_w\right)}_1$ , $8\text{in}$ for $b_1$ , $0.52\text{in}$ for $t_1$ , $14.3\text{in}$ for ${\left(h_w\right)}_1$ in the Equation (I)

  $\begin{array}{c}{I}_1=881{\text{in}}^4+2\times \left[\frac{8\text{in}{\left(0.52\text{in}\right)}^3}{12}+\left(8\text{in}\right)\left(0.52\text{in}\right){\left(\frac{14.3\text{in}}{2}+\frac{0.52\text{in}}{2}\right)}^2\right]\\ =881{\text{in}}^4+2\left(0.937{\text{in}}^4+228.42{\text{in}}^4\right)\\ =1339.71{\text{in}}^4\end{array}$

Substitute $0.52\text{in}$ for $t_1$ and $14.3\text{in}$ for ${\left(h_w\right)}_1$ in the Equation (II).

  $\begin{array}{c}{h}_1=14.3\text{in}+2\times 0.52\text{in}\\ =14.3\text{in}+1.04\text{in}\\ =15.34\text{in}\end{array}$

Substitute $24\text{in}$ for ${\left(A_w\right)}_1$

  $8\text{in}$ for $b_1$ , and $0.52\text{in}$ for $t_1$ in the Equation (III).

  $\begin{array}{c}{A}_1=24\text{in}+2\times \left(8\text{in}\times 0.52\text{in}\right)\\ =24{\text{in}}^2+8.32{\text{in}}^2\\ =32.32{\text{in}}^2\end{array}$

Substitute $1339.71{\text{in}}^4$ for $I_1$ , $15.34\text{in}$ for $h_1$ in the Equation (IV).

  $\begin{array}{c}{S}_1=\frac{2\times 1339.71{\text{in}}^4}{15.34\text{in}}\\ =2\times 87.33{\text{in}}^3\\ =174.66{\text{in}}^3\end{array}$

Refer Table-F-4(a) “Properties of wide equal legs L-shape channel” $L6\times 6\times \frac{1}{2}$ to obtain

  $A_a$ as $5.77{\text{in}}^2$ , $I_a$ as $19.9{\text{in}}^4$ , $b_2$ as $0.675\text{in}$ , $t_2$

  $19.9{\text{in}}^4$ , and $C_a$ as $1.67\text{in}$ .

Substitute $0.675\text{in}$ for $b_2$ , $14\text{in}$ for $t_2$ , $19.9{\text{in}}^4$ for $I_a$ , $5.77{\text{in}}^2$ for $A_a$ and $1.67\text{in}$ for $C_a$ in the Equation (V).

  $\begin{array}{c}{I}_2=\frac{\left(0.675\text{in}\right){\left(14\text{in}\right)}^3}{12}+4\left[19.9{\text{in}}^4+5.77{\text{in}}^2{\left(\frac{14\text{in}}{2}-1.67\text{in}\right)}^2\right]\\ =154.35{\text{in}}^4+4\left(19.9{\text{in}}^4+163.92{\text{in}}^4\right)\\ =889.62{\text{in}}^4\end{array}$

Substitute $0.675\text{in}$ for $b_2$ , $14\text{in}$ for $t_2$ , and $5.77{\text{in}}^2$ for $A_a$ in the Equation (VI).

  $\begin{array}{c}{A}_2=4\left(5.77{\text{in}}^2\right)+\left(14\text{in}\right)\left(0.675\text{in}\right)\\ =23.08{\text{in}}^2+9.45{\text{in}}^2\\ =32.53{\text{in}}^2\end{array}$

Substitute $889.62{\text{in}}^4$ for $I_2$ and $14\text{in}$ for $h_2$ in the Equation (VII).

  $\begin{array}{c}{S}_2=\frac{2\times 889.62{\text{in}}^4}{14\text{in}}\\ =2\times 63.54{\text{in}}^3\\ =127.09{\text{in}}^3\end{array}$

Refer Table-F-3(a) “Properties of C-shape channel” for $C15\times 150$ to obtain $h_c$ as $15\text{in}$ , $t_3$ as $0.375\text{in}$ , $I_c$ as $404{\text{in}}^4$ , $b_3$ as $4\text{in}$ , $A_c$ as $14.7{\text{in}}^2$ .

Substitute $15\text{in}$ for $h_c$ and $0.375\text{in}$ for $t_3$ . in the Equation (VIII).

  $\begin{array}{c}{h}_3=15\text{in}+2\times \left(0.375\text{in}\right)\\ =15\text{in}+0.75\text{in}\\ =15.75\text{in}\end{array}$

Substitute $404{\text{in}}^4$ for $I_c$ , $4\text{in}$ for $b_3$

  $4\text{in}$ for $t_3$ and $15\text{in}$ for $h$ in the Equation (IX).

  $\begin{array}{c}{I}_3=2\times 404{\text{in}}^4+2\left[\frac{4\text{in}{\left(0.375\text{in}\right)}^3}{112}+\left(4\text{in}\times 0.375\text{in}\right){\left(\frac{15\text{in}}{2}+\frac{0.375\text{in}}{2}\right)}^2\right]\\ =808{\text{in}}^4+2\left[0.0176{\text{in}}^4+88.65{\text{in}}^4\right]\\ =808{\text{in}}^4+177.33{\text{in}}^4\\ =985.33{\text{in}}^4\end{array}$

Substitute $14.7{\text{in}}^2$ for $A_c$ , $4\text{in}$ for $b_3$ and $4\text{in}$ for $t_3$ in the Equation (X).

  $\begin{array}{c}{A}_3=2\left(14.7{\text{in}}^2\right)+2\left(4\text{in}\right)\left(0.375\text{in}\right)\\ =29.4{\text{in}}^2+3{\text{in}}^2\\ =32.4{\text{in}}^2\end{array}$

Substitute $985.33{\text{in}}^4$ for $I_3$ and $15.75\text{in}$ for $h_3$ in the Equation (XI).

  $\begin{array}{c}{S}_3=\frac{2\times 985.33{\text{in}}^4}{15.75\text{in}}\\ =2\times 62.56{\text{in}}^3\\ =125.12{\text{in}}^3\end{array}$

Since stress due to moment is inversely proportional to section modulus, therefore the beam which has the highest section modulus will have the highest capacity.

The value of the section modulus of the beam-1 is highest i.e., $\left(S_1=174.66{\text{in}}^3\right)$

Conclusion:

The beam of the largest momentum capacity. is beam-1.