Chapter 5, Problem 46P

A clinical trial was conducted to test the efficacy of nifedipine, a new drug for reducing chest pain in patients with angina severe enough to require hospitalization. The duration of the study was 14 days in the hospital unless the patient was withdrawn prematurely from therapy, was discharged from the hospital, or died prior to this time. Patients were randomly assigned to either nifedipine or propranolol and were given the same dosage of each drug in identical capsules at level 1 of therapy. If pain did not cease at this level of therapy or if pain recurred after a period of pain cessation, then the patient progressed to level 2, whereby the dosage of each drug was increased according to a pre-specified schedule. Similarly, if pain continued or recurred at level 2, then the patient progressed to level 3, whereby the dosage of the anginal drug was increased again. Patients randomized to either group received nitrates in any amount deemed clinically appropriate to help control pain.

The main objective of the study was to compare the degree of pain relief with nifedipine vs. propranolol. A secondary objective was to better understand the effects of these agents on other physiologic parameters, including heart rate and blood pressure. Data on these latter parameters are given in Data Set NIFED.DAT (at www.cengagebrain.com); the format of this file is shown in Table 5.3

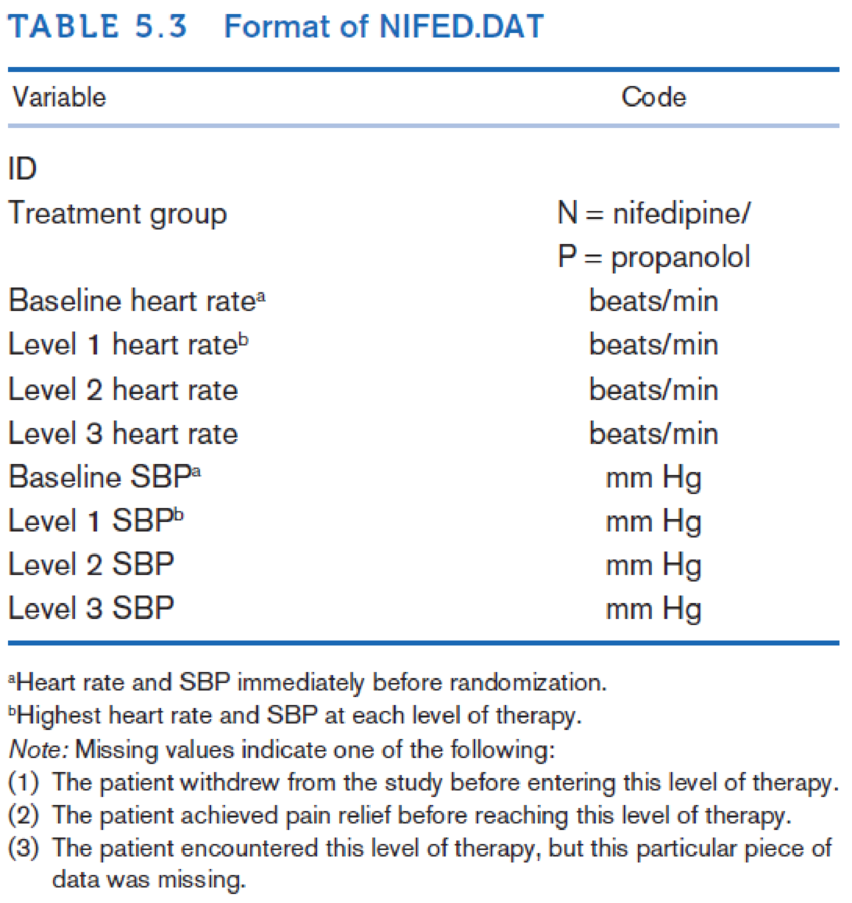
Compare graphically the effects of the treatment regimens on heart rate and blood pressure. Do you notice any difference between treatments?