
Concept explainers
A 1.00-kg glider on a horizontal air track is pulled by a string at an angle θ. The taut string runs over a pulley and is attached to a hanging object of mass 0.500 kg as shown in Figure P5.40. (a) Show that the speed vx of the glider and the speed vy of the hanging object are related by vx = uvy, where u = z(z2 − h02)−1/2. (b) The glider is released from rest. Show that at that instant the acceleration ax of the glider and the acceleration ay of the hanging object are related by ax = uay. (c) Find the tension in the string at the instant the glider is released for h0 = 80.0 cm and θ = 30.0°.
Figure P5.40
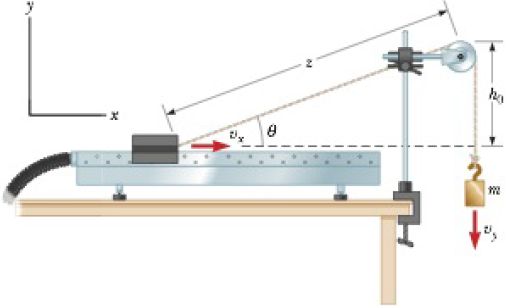
(a)
The relation between the speed of the glider and the speed of the hanging object.
Answer to Problem 40AP
The relation between the speed of the glider and the speed of the hanging object is
Explanation of Solution
The mass of the glider is
The free body diagram of the given case is as shown below.
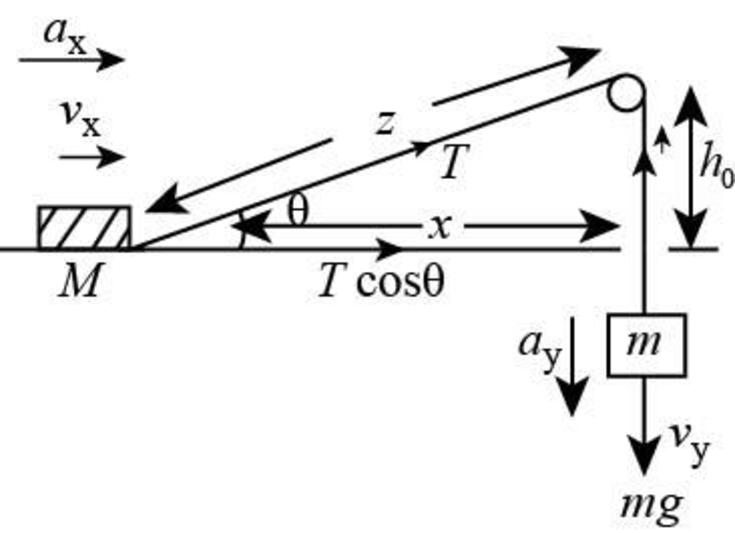
Figure (1)
Form the above figure (1).
Write the expression for the length of the string using Pythagorean Theorem,
Here,
Rearrange the above equation for
Write the expression for the speed of the glider
Here,
Substitute
The term
Write the expression for the speed of the hanging object.
Here,
Substitute
Substitute
Conclusion:
Therefore, the relation between the speed of the glider and the speed of the hanging object is
(b)
The relation between the acceleration of the glider and the speed of the hanging object.
Answer to Problem 40AP
The relation between the acceleration of the glider and the speed of the hanging object is
Explanation of Solution
From equation (2), the relation of
Write the expression for the acceleration of the glider
Substitute
The initial velocity of the hanging object is zero.
Substitute
Here,
Conclusion:
Therefore, the relation between the acceleration of the glider and the speed of the hanging object is
(c)
The tension of the string.
Answer to Problem 40AP
The tension of the string is
Explanation of Solution
From the free body diagram in figure (1) the net direction in
From part (a) the value of
Substitute
Substitute
Thus, the value of
The net force in
Here,
Substitute
Rearrange the above equation for
The net force in the
Here,
Form part (b) substitute
From equation (3) substitute
Conclusion:
Substitute
Therefore, the tension in the string is
Want to see more full solutions like this?
Chapter 5 Solutions
Physics for Scientists and Engineers
- 12. What could we conclude if a system has a phase trajectory that sweeps out larger and larger area as time goes by?arrow_forwardneed help part darrow_forwardA cab driver heads south with a steady speed of v₁ = 20.0 m/s for t₁ = 3.00 min, then makes a right turn and travels at v₂ = 25.0 m/s for t₂ = 2.80 min, and then drives northwest at v3 = 30.0 m/s for t3 = 1.00 min. For this 6.80-min trip, calculate the following. Assume +x is in the eastward direction. (a) total vector displacement (Enter the magnitude in m and the direction in degrees south of west.) magnitude direction For each straight-line movement, model the car as a particle under constant velocity, and draw a diagram of the displacements, labeling the distances and angles. Let the starting point be the origin of your coordinate system. Use the relationship speed = distance/time to find the distances traveled during each segment. Write the displacement vector, and calculate its magnitude and direction. Don't forget to convert min to s! m Model the car as a particle under constant velocity, and draw a diagram of the displacements, labeling the distances and angles. Let the…arrow_forward
- î A proton is projected in the positive x direction into a region of uniform electric field E = (-5.50 x 105) i N/C at t = 0. The proton travels 7.20 cm as it comes to rest. (a) Determine the acceleration of the proton. magnitude 5.27e13 direction -X m/s² (b) Determine the initial speed of the proton. 8.71e-6 magnitude The electric field is constant, so the force is constant, which means the acceleration will be constant. m/s direction +X (c) Determine the time interval over which the proton comes to rest. 1.65e-7 Review you equations for constant accelerated motion. sarrow_forwardThree charged particles are at the corners of an equilateral triangle as shown in the figure below. (Let q = 2.00 μC, and L = 0.750 m.) y 7.00 με 60.0° L 9 -4.00 μC x (a) Calculate the electric field at the position of charge q due to the 7.00-μC and -4.00-μC charges. 112 Once you calculate the magnitude of the field contribution from each charge you need to add these as vectors. KN/CI + 64 × Think carefully about the direction of the field due to the 7.00-μC charge. KN/Cĵ (b) Use your answer to part (a) to determine the force on charge q. 240.0 If you know the electric field at a particular point, how do you find the force that acts on a charge at that point? mN Î + 194.0 × If you know the electric field at a particular point, how do you find the force that acts on a charge at that point? mNarrow_forwardIn the Donkey Kong Country video games you often get around by shooting yourself out of barrel cannons. Donkey Kong wants to launch out of one barrel and land in a different one that is a distance in x of 9.28 m away. To do so he launches himself at a velocity of 22.6 m/s at an angle of 30.0°. At what height does the 2nd barrel need to be for Donkey Kong to land in it? (measure from the height of barrel 1, aka y0=0)arrow_forward
- For which value of θ is the range of a projectile fired from ground level a maximum? 90° above the horizontal 45° above the horizontal 55° above the horizontal 30° above the horizontal 60° above the horizontalarrow_forwardA map from The Legend of Zelda: The Breath of the Wild shows that Zora's Domain is 7.55 km in a direction 25.0° north of east from Gerudo Town. The same map shows that the Korok Forest is 3.13 km in a direction 55.0° west of north from Zora's Domain. The figure below shows the location of these three places. Modeling Hyrule as flat, use this information to find the displacement from Gerudo Town to Korok Forest. What is the magnitude of the displacement? Find the angle of the displacement. Measure the angle in degrees north of east of Gerudo Town.arrow_forwardRace car driver is cruising down the street at a constant speed of 28.9 m/s (~65 mph; he has a “lead” foot) when the traffic light in front of him turns red. a) If the driver’s reaction time is 160 ms, how far does he and his car travel down the road from the instant he sees the light change to the instant he begins to slow down? b) If the driver’s combined reaction and movement time is 750 ms, how far do he and his car travel down the road from the instant he sees the light change to the instant he slams on her brakes and car begins to slow down? c) If the driver’s average rate of acceleration is -9.5 m/s2 as he slows down, how long does it take him to come to a stop (use information about his speed of 28.9 m/s but do NOT use his reaction and movement time in this computation)? Please answer parts a-c. Show all work. For each question draw a diagram to show the vector/s. Show all the step and provide units in the answers. Provide answer to 2 decimal places unless stated otherwise.arrow_forward
- Below you will find 100 m split times for the American and France men’s 4x100 meter free style relay race during the 2008 Beijing Summer Olympics). Answer questions a-d. a) What was the total race time for each team, in seconds? b) Which team won the race? What was the difference in the teams’ times? c) What was the average speed for each team for the whole race? (provide answer to 3 decimal places). d) Calculate the average speed for each swimmer and report the results in a table like the one above. Remember to show the calculation steps. (provide answer to 3 decimal places). PLEASE SHOW ALL WORK AND STEPS.arrow_forwardNeed complete solution Pleasearrow_forwardBelow you will find 100 m split times for the American and France men’s 4x100 meter free style relay race during the 2008 Beijing Summer Olympics). Fill out the chart below. Calculate average speed per split (m/s). Show all work.arrow_forward
 Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





